p-value based multiple testing with side information

부가정보(side information)을 활용한 p-value 기반의 다중 검정모델인 AdaPT와 IHW를 다뤄볼 예정이다.

AdaPT

Lei, L. & Fithian, W. (2018). Adapt: an interactive procedure for multiple testing with side information

현대 통계학에서는 가설 검정 시 p-value 외에도 각 가설의 맥락을 설명하는 풍부한 부가 정보(e.g. 유전자 순위, 신호 강도)가 주어지는 경우가 많다. 기존의 BH와 같은 절차들은 이러한 정보를 활용하지 않아 더 많은 것을 발견할 기회를 놓칠 수 있다. AdaPT는 분석가가 데이터와 상호작용하며 탐색적으로 최적의 분석 방법을 찾아가는 현대 데이터 분석의 패러다임을 지원한다. 미리 정해진 알고리즘을 따르는 대신, 분석가는 매 단계에서 정보를 얻으며 다음 전략을 수정할 수 있다.

\(\{(p_i, x_i) \in [0,1] \times \mathcal{X}\}_{i=1}^n\)을 이용하여 반복적으로 부가 정보(side information)를 반영한 임계값을 설정하는 방법이다.

매 스텝 $t$에서 임계값 $s_t(x)$를 계산하여, 이 임계값으로 가설을 기각했을 때에 가짜 발견의 비율의 추정값 $\hat{FDP}_t$를 계산한다.

\(\hat{FDP}_t \leq \alpha\)를 만족할 때 까지 이를 반복한다. 만약, 이를 만족하면 반복을 멈추고, 정지 스텝(stopping time) $\hat{t}$에서 \(p_i \leq s_{\hat{t}}(x_i)\)인 가설들을 기각한다.

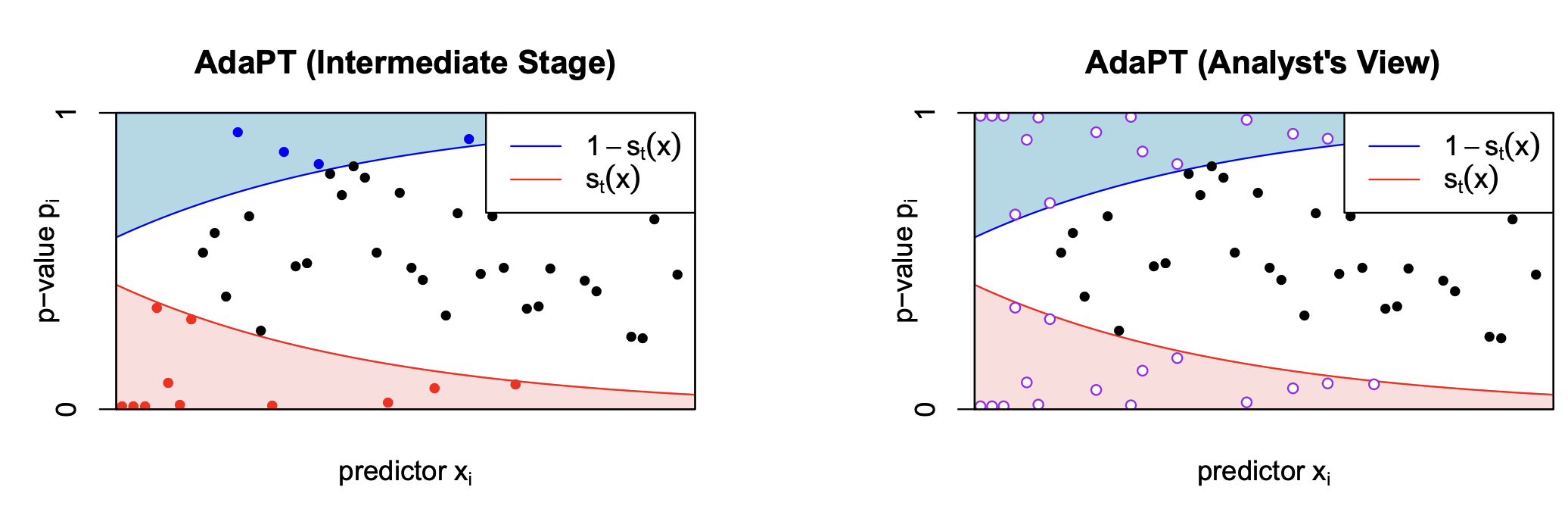
그림과 같이 임계값 $s_t(x_i)$가 부가정보 $x_i$의 관한 함수로 정의되며, $p_i$가 $1-s_t(x_i)$, $s_t(x_i)$를 기준으로 3가지 영역으로 구분된다.

$s_t(x)$가 결정되면, $\hat{FDP}_t$는 다음과 같이 계산할 수 있다.

\[\hat{FDP}_t = \frac{1+ A_t}{\max(1, R_t)}\]

• $R_t = | {i:p_i\leq s_t(x_i)}|$ : 기각된 가설의 수이다. 위에서 빨간 구역에 속하는 p-value의 수이다.
• $A_t = | {i:p_i\geq 1-s_t(x_i)}|$ : 위에서 파란 구역에 속하는 p-value의 수이다. 이를 가짜 발견의 추정값으로 사용하는 이유는 귀무가설 하의 p-value가 균등분포를 따를 것이란 가정 때문이다.

가짜 기각인 경우는 귀무가설인 $p_i$가 $s_t(x_i)$보다 작거나 같을 경우이다. 하지만 관측가능한 $p_i$는 귀무가설과 대립가설간의 결합확률분포로부터 주어짐으로, 이를 구할 수 없다.

하지만, 일반적으로 대립가설하의 p-value 확률분포는 귀무가설하에서보다 확률적으로 작게 가정하기에, 파란색부분의 $1-s_t(x_i)$보다 큰 $p_i$들은 귀무가설 하의 $p_i$들만 존재할 가능성이 높다. 또한, 귀무 가설하의 p value를 균등분포로 가정하면, 이는 가짜 기각의 확률로 사용할 수 있다. 여기에 보수적으로 1을 더해 $1+A_t$를 가짜 기각의 수의 추정값으로 사용한다.

이제 \(\hat{FDP}_t > \alpha\)이면, 분석가는 새로운 임계값 $s_{t+1}(x)$를 설정한다. 임계값은 \(s_{t+1}(x) \preceq s_{t}(x)\)가 되도록 업데이트 되어야 한다. 다시 말해서, 모든 $x \in \mathcal{X}$에 대해서, \(s_{t+1}(x) \leq s_{t}(x)\) 즉, 더 엄격하게 기각역이 정해짐으로, 가짜 기각의 비율 $FDP$는 감소한다.

오른쪽 그림은 임계값을 설정하는 분석가(analyst)가 접근할 수 있는 정보이다. 분석가는 현재 스텝 $t$의 정보를 기반으로 다음 스텝의 임계값 $s_{t+1}(x)$를 설정하는데에 있어서 왼쪽 그림에서의 실제 p-value가 아닌, 빨강/파랑색 부분에 속하는 p-value들을 구분하지 못하도록, 보간한 p-value들에 대해 접근할 수 있다.

이는 위에서 가짜 기각의 수를 파란색 영역에 속한 p-value들의 수로 추정했기 때문이다. 만약, 분석가가 실제 빨강/파란색 부분에 속하는 p-value를 구별할 수 있다면, 데이터의 패턴마다 $R_t$를 최대화하고, $A_t$를 최소화하는 방향으로 임계값을 설정할 것이고, 이는 원래 목적인 $\hat{FDP}$가 $FDP$에 대한 추정을 과소평가하게 만들것이고, 추정치의 기댓값이 실제 값보다 작아지는 편향이 발생할 것이다. 따라서, $\hat{FDP} \leq \alpha$일 때, 가설을 기각하더라도, 실제 $FDP$가 $\alpha$이하로 통제함을 보장할 수 없다.

매 스텝 $t$에서 분석가가 접근할 수 있는 p-value를 \(\tilde{p}_{ti}\)라고 하면, \(p_i < s_t(x_i)\)또는 \(p_i \geq 1-s_t(x_i)\)인 경우 \(\tilde{p}_{ti} = \{p_i, 1-p_i\}\)로 주어지고, 이외에는 \(\tilde{p}_{ti} = p_i\)이다.

AdaPT 모델 가정

인덱스 집합 $[n] = {1,…,n}$에 대해 각각의 가설 $H_i, \ i \in [n]$에 대해 $(p_i,x_i) \in \mathcal{X} \times[0,1]$이 관측된다. $\mathcal{H}_0$을 귀무가설인 가설들의 집합이라고 하고, ${p_i: i\in \mathcal{H}_0}$의 각 원소들은 서로 독립이고, ${p_i: i \notin \mathcal{H}_0}$와도 독립이라고 가정하자. 즉, 대립가설 하의 p-value끼리는 상호 독립 가정을 하지 않는다.

순열검정이나 이산형 검정통계량을 이용한 검정과 같이 여러 다중검정의 경우에서 귀무가설하의 p-value가 균등분포를 따르지 않을 수 있다. AdaPT에서는 이보다 더 완화된 제약인 귀무 p-value가 mirror-conservative이면, FDR 통제가 가능함을 보일 것이다.

[Definition] $p_i$가 다음을 만족하면 mirror-conservative하다고 한다.

\[Pr_{H_i}(p_i \in [a_1,a_2]) \leq Pr_{H_i}(p_i \in [1-a_2,1-a_1]), \ \forall 0\leq a_1\leq a_2 \leq 0.5\]

e.g. $p_i \sim Ber(\pi)$인 경우 $Pr(p_i=0) \leq Pr(p_i=1)$을 만족할 경우, mirror conservative임으로 성공확률 $\pi$에 대해 $1-\pi \leq \pi$, 즉, $\pi \geq 0.5$를 만족하는 베르누이 시행에 대해서는 mirror-conservative하다.

Note. 가짜 기각의 수를 기각 구간의 위로 대칭인 구간으로 추정하고, 위로 대칭인 곳에서 더 높은 확률 값을 갖으므로, $A_t$는 충분히 보수적으로 가짜 기각의 수를 추정할 수 있을 것이다.

AdaPT의 FDR 통제에 대한 증명은 확률 과정, 특히 마팅게일 이론을 바탕으로 한다. AdaPT는 시간(스텝)에 따라 분석가의 정보가 변하고, 그 정보에 기반해 멈춤을 결정하는 동적인 절차이기 때문이다.

AdaPT는 스텝 $t$가 진행됨에 따라 p-value의 마스킹이 점차 해제되면서 분석가가 접근할 수 있는 정보가 점진적으로 증가한다. 이처럼 시간에 따라 누적되는 정보의 흐름을 다음과 같이 정의한다.

[Definition] 확률 공간 $(\Omega, \mathcal{A}, Pr)$가 주어졌을 때, 인덱스 집합 $T = {0,1,2,…}$에 대한 filteration ${\mathcal{F}_t: t \in T}$은 다음과 같이 정의된다.

1. 임의의 $t \in T$에 대해 $\mathcal{F}_t$는 $\mathcal{A}$의 부분 시그마 필드이다.
2. $s,t \in T$이고, $s \leq t$이면, $\mathcal{F}_s \subset \mathcal{F}_t$이다.

다음과 같이 매 스텝 $t=0,1,2,…$마다, 분석가가 접근할 수 있는 정보 $\mathcal{F}_t$를 부가정보, 마스킹된 p-value, 파란/빨간 영역에 속한 p-value들의 수에대한 시그마 필드로 정의한다.

\[\mathcal{F}_t = \sigma(\{x_i,\tilde{p}_{ti}\}_{i=1}^n, A_t, R_t)\]

초기 상태의 정보는 임계값이 0.5인 상태, 즉 모든 p-value가 마스킹된 정보 \(\mathcal{F}_{-1} = \sigma(\{x_i,(p_i,1-p_i)\}_{i=1}^n)\). 이제 임계값은 이전 스텝의 정보를 통해 계산됨으로 \(s_{t+1} \in \mathcal{F}_t\)이다. 또한, \(s_{t+1} \preceq s_t\)가 되도록 임계값을 설정함으로, 마스킹된 p-value의 수는 점차 줄어든다.

수학적 귀납법을 통해 임의의 $u \leq t$이면, \(\mathcal{F}_u \subset \mathcal{F}_{t}\)임을 보일 수 있다, 부가정보와 마스킹된 p-value에 대해서는 자명하고, $u=-1$인 경우에 대해서도 이는 자명함으로, \(\mathcal{F}_{u-1} \subset \mathcal{F}_t\)를 만족하는 경우의 $A_u, R_u$에 대해서만 보이면 충분하다.

이 경우, 임계값 $s_u \subset \mathcal{F}_{u-1} \subset \mathcal{F}_t$임으로, 이를 통해 계산되는 $A_u, R_u$또한 $\mathcal{F}_t$를 통해 계산이 가능하다. 따라서, $\mathcal{F}_u \subset \mathcal{F}_t$가 성립한다. 즉, ${\mathcal{F}_t:t=-1,0,…}$는 포함관계가 커지는 시그마 필드열이다.

따라서, ${\mathcal{F}_t}$는 filteration이다. 다시말해서, 정보가 시간이 지남에 따라 감소하지 않고, 누적되거나 유지된다.

[Defintion] 이산 확률과정 ${X_t}$는 다음을 만족할 때 filteration ${\mathcal{F}_t}$에 대한 마팅게일(martingale)이라고 한다.

1. 적응성 (Adaptedness): 모든 $X_t$는 $\mathcal{F}_t$에서 측정가능하다. 다시말해서, $\mathcal{F}_t$의 정보만으로 결정된다. 따라서, $\mathbb{E}[X_t|\mathcal{F}_t] = X_t, \ \forall t$가 성립한다.

2. 적분가능성 (Integrability): \(\mathbb{E}[X_t] < \infty, \ \forall t\)

3. 마팅게일 속성( Martingale Property): \(\mathbb{E}[X_{t+1} \mid \mathcal{F}_t] = X_{t}, \ \forall t\). 만약, \(\mathbb{E}[X_{t+1} \mid \mathcal{F}_t] \leq X_{t-1}\)를 만족하면, 이는 ${\mathcal{F}_t}$에 대한 슈퍼마팅게일이라고 한다. 이는 미래의 기댓값이 현재보다 크지 않음을 의미하며 불리한 게임에 비유한다.

Note. $\mathbb{E}[X_t|\mathcal{F}_t]$는 다음 조건을 만족하는 거의 확실하게 유일한 확률변수 $Y$이다.

1. $Y$는 $\mathcal{F}_t$에서 측정가능하다.
2. $\int_A YdPr = \int_A XdPr \ \forall A \in \mathcal{F}_t$

마팅게일 속성은 현재 시점 $t$에서 모든 정보를 고려할 때, 즉 $\mathcal{F}_t$가 주어졌을 때, 확률과정의 기댓값은 변함이 없음을 의미한다. \(\mathbb{E}[X_{t+1} - X_t\mid\mathcal{F}_t] = \mathbb{E}[X_{t+1}\mid\mathcal{F}_t] - X_t = X_t-X_t = 0\)

또한, filteration은 포함관계가 커지는 시그마 필드열임으로, 임의의 $m<n$에 대해 다음을 만족한다.

\[\mathbb{E}[X_n \mid \mathcal{F}_m] = \mathbb{E}[\mathbb{E}[X_n|\mathcal{F}_{n-1}]\mid\mathcal{F}_m] = \mathbb{E}[X_{n-1}\mid \mathcal{F}_{m}] = ... = \mathbb{E}[X_{m}\mid \mathcal{F}_{m}] = X_m\]

[Definition] Filteration ${\mathcal{F_t}: t \in T}$가 주어졌을 때, 확률 변수 $\tau: \Omega \rightarrow T \cup {\infty}$가 다음을 만족하면, $\tau$를 ${\mathcal{F}_t}$의 중지 시간(stopping time)이라고 부른다.

\[\forall t \in T, \ \{\tau \leq t\} \subset \mathcal{F}_t\]

다시 말해서, 정지시간이란 어떤 과정을 중단하는 시점을 나타내는 확률 변수로, 미래의 정보를 미리 보지 않고 오직 과거와 현재의 정보만으로 멈춤을 결정해야 한다.

Adapt에서는 중지 시간을 $\hat{t} = \min{t: \hat{FDP}_t \leq \alpha}$로 정의함으로, $\mathcal{F}_t$의 정보만으로 결정할 수 있는 규칙이기에 유효한 중지 시간이다.

[Theorem] 선택적 중지 정리 (Optional Stopping Theorem)

${X_t}$가 슈퍼 마팅게일이고, $\tau$가 중지시간이라고 하자. 만약 조건 중 하나 이상을 만족한다면,

1. $\tau$는 거의 확실하게 유계이다.
2. $\tau$가 거의 확실하게 유한하고, $\mathbb{E}[X_{\tau}] < \infty$
3. $\tau$가 거의 확실하게 유한하고, 모든 $t$에 대해 \(\mathbb{E}[\|X_{t+1} - X_t\| \mid \mathcal{F}_t]\)가 유계이다.

정지 시간 $\tau$에서의 기댓값은 시작 시점의 기댓값보다 작거나 같다. $\mathbb{E}[X_{\tau}] \leq \mathbb{E}[X_0]$

즉, 불리한 게임에서는 아무리 영리한 중단 규칙을 사용하더라도, 평균적으로는 시작점보다 더 나은 결과를 얻을 수 없다.

AdaPT에서는 적절한 슈펴마팅게일이 되는 ${Z_t}$와 중지 시간 $\hat{t}$를 이용하여, FDR 통제를 증명한다.

FDR 통제

다음과 같이 특정 스텝 $t$에서 파란 영역에 속한 귀무 가설하의 p-value, 빨간 영역에 속한 귀무 가설하의 p-value의 수를 각각 $U_t, V_t$라고 정의한다. 즉,

\[\begin{align*} U_t &= \sum_{p_i \in \mathcal{H}_0}I(p_i \geq 1-s_t(x_i)\} \\ V_t &= \sum_{p_i \in \mathcal{H}_0}I(p_i \leq s_t(x_i)\} \end{align*}\]

Note. $V_t$는 가짜 발견의 수이다. 이와 대칭인 $U_t$에 대한 상한 $A_t$으로 가짜 발견의 수를 추정한다.

Note. $U_t \leq A_t$이며, $s_t(x)$는 0.5에서 시작하여, 점점 감소함으로 $V_t$는 빨간 영역중에 p-value가 0.5보다 작은 p-value들의 수, $U_t$는 파란 영역중에 p-value가 0.5보다 크거나 같은 p-value들의 수이다.

따라서, $b_i = I(p_i \geq 0.5),$ $\mathcal{C}_t = {i \in \mathcal{H}_0 : p_i \notin (s_t(x_i), 1-s_t(x_i))}$를 이용하여 $U_t, V_t$를 다음과 같이 쓸 수 있다.

\[\begin{align*} U_t &= \sum_{i \in \mathcal{C}_t}b_i \\ V_t &= |\mathcal{C}_t| - U_t \end{align*}\]

또한 $m_i = \min(p_i, 1-p_i)$를 이용하면, p-value $p_i$를 다음과 같이 분해할 수 있다.

\[p_i = (1-b_i)m_i + b_i(1-m_i)\]

Note. $(b_i, m_i)$를 아는 것은 $p_i$의 정보를 아는 것과 같고, $b_i$는 0 또는 1의 값을 갖으므로, 베르누이 시행으로 모델링할 수 있다.

만약 귀무가설하의 p-value가 균등 분포를 따른다면, 어떤 $s_t$를 선택하더라도 $U_t \approx V_t$를 만족하며,

\[\hat{FDP}_t = \frac{1+A_t}{\max(R_t,1)} > \frac{U_t}{\max(R_t,1)} \approx \frac{V_t}{\max(R_t,1)} = FDP_t\]

이다.

보조정리

$b_1,…,b_n$이 시그마 필드 $\mathcal{G}_{-1}$하에서 독립이고, 성공확률 $\rho_i$인 베르누이 시행을 따르며, 거의 확실하게 $\min_i \rho_i \geq \rho$인 $\rho>0$가 존재한다고 가정하자. 즉,

\[\begin{align*} Pr(b_i = 1|\mathcal{G}_{-1}) &= \rho_i, \\ Pr(\rho_i \geq \rho>0, \ \forall i)&=1 \end{align*}\]

또한 인덱스 집합 $[n] = {1,…,n}$내의 포함관계가 작아지는 측정가능한 부분집합열 ${\mathcal{C}_t}$과 이에 대한 시그마 필드 $\mathcal{G}_t$를 다음과 같이 가정하자.

\[\mathcal{G}_t = \sigma(\mathcal{G}_{-1}, \mathcal{C}_t, \{b_i\}_{i \notin \mathcal{C}_t}, \sum_{i \in \mathcal{C}_t} b_i)\]

이제, filteration ${\mathcal{G}_t:t\geq 0}$에 대해 거의 확실하게 유한인 정지 시간 $\hat{t}$가 존재하면, 다음의 부등식이 만족한다.

\[\mathbb{E}[\frac{1+|\mathcal{C}_{\hat{t}}|}{1+\sum_{i \in \mathcal{C}_{\hat{t}}}b_i} | \mathcal{G}_{-1}] \leq \frac{1}{\rho}\]

증명과정은 대략 아래와 같은 절차로 진행된다.

1. Barber and Candes (2016)의 증명과정과 유사하게 서로 다른 성공 확률을 갖는 $b_1,…,b_n$을 쉽게 다룰 수 있도록 보조 함수 $\mathcal{A} \in [n]$를 도입하여, 이를 포함한 시그마 필드 \(\mathcal{G}_t^{\mathcal{A}} \subset \mathcal{G}_t\)를 적절히 정의하여 augmented filteration \(\{\mathcal{G}_t^{\mathcal{A}}\}\)를 구성한다. 이제, $\mathbb{E}[\cdot \mid \mathcal{G}_{-1},\mathcal{A}]$에 대한 부등식을 유도한다.

2. 조건부 기댓값 내의 식이 복잡하므로, 모든 $t>0$마다, \(Z_t^{\mathcal{A}} \geq \frac{1+\mid \mathcal{C}_{\hat{t}} \mid }{1+\sum_{i \in \mathcal{C}_{\hat{t}}}b_i}\)이고, 이러한 확률변수열이 $\mathcal{G}_t^{\mathcal{A}}$에서 슈퍼 마팅게일(super-martingale)이 되도록 하는 $Z_t^{\mathcal{A}}$를 적절히 정의할 수 있다.

3. $\mathcal{G}_t \subset \mathcal{G}_t^{\mathcal{A}}$임으로 $\hat{t}$ 는 $\mathcal{G}_t^{\mathcal{A}}$의 중지 시간이기도 하다. 또한$\mathcal{G}_t \subset \mathcal{G}_t^{\mathcal{A}}$${ Z_t^{\mathcal{A}} }$은 슈퍼 마팅게일임으로 선택적 중지 정리(optimal scoring theorem)에 의해 다음의 관계식이 만족한다.

   \[\mathbb{E}[\frac{1+\mid \mathcal{C}_{\hat{t}}\mid}{1+\sum_{i \in \mathcal{C}_{\hat{t}}}b_i} | \mathcal{G}_{-1}, \mathcal{A}] \leq \mathbb{E}[Z_t^{\mathcal{A}} | \mathcal{G}_{-1}, \mathcal{A}] \leq \mathbb{E}[Z_0^{\mathcal{A}} | \mathcal{G}_{-1}, \mathcal{A}] = \mathbb{E}[Z_0^{\mathcal{A}} | \mathcal{G}_{-1}], \ \forall \mathcal{A}\]

4. 이제, $\mathbb{E}[Z_0^{\mathcal{A}} \mid \mathcal{G}_{-1}] \leq \rho^{-1}$임을 보여, 위 부등식에서 $\mathcal{A}$를 주변화하면 최종 부등식을 구할 수 있다.

이제 귀무가설 하의 p-value들은 상호 독립인 mirror conservative한 분포를 따르고 또한, 대립가설 하의 p-value 집단과도 독립이라고 할 때, 보조정리를 이용하여 AdaPT가 FDR을 $\alpha$이하로 통제함을 보이자.

먼저 위에서 보인것과 같이 $p_i$를 베르누이 시행 $b_i$와 $m_i$로 분해하여, 위의 보조 정리를 사용할 수 있도록 ${\mathcal{G}_t}$를 다음과 같이 정의한다.

\[\mathcal{G}_{-1} = \sigma((x_i,m_i)_{i=1}^n, (b_i)_{i \notin \mathcal{H}_0}), \ \mathcal{G}_t = \sigma(\mathcal{G}_{-1}, \mathcal{C}_t, (b_i)_{i \notin \mathcal{H}_0}, U_t)\]

\(\mathcal{G}_t\)를 통해 마스킹되지 않은 $p_i$들의 인덱스는 \(\mathcal{C}_t\)로, 대응하는 값은 $m_i$와 \((b_i)_{i \notin \mathcal{H}_0}\)로 알아낼 수 있으며, $\mathcal{F}_t$의 나머지 원소들도 다음과 같으며, 마지막 항들은 $\mathcal{C}_t$와 $m_i$로 알 수 있는 정보임으로, $\mathcal{G}_t$에 포함된다.

\[\begin{align*} A_t &= U_t + \mid\{i \notin \mathcal{H}_0: p_i \geq 1-s_t(x_i)\}\mid \\ R_t &= |\mathcal{C}_t| - U_t + \mid\{i \notin \mathcal{H}_0: p_i \leq s_t(x_i)\}\mid \end{align*}\]

따라서, 모든 $t$에 대해 $\mathcal{F}_t \subset \mathcal{G}_t$임으로, 중지 시간 $\hat{t}= \min {t: \hat{FDR}_t \leq \alpha}$ 또한 filteration ${\mathcal{G}_t}$에 대한 중지 시간이다.

AdaPT의 중지 시간 $\hat{t}$에 대해 다음이 성립한다.

\[\begin{align*} FDP_{\hat{t}} &= \frac{V_{\hat{t}}}{\max(R_{\hat{t}},1)} = \frac{1+U_{\hat{t}}}{\max(R_{\hat{t}},1)}\cdot \frac{V_{\hat{t}}}{1+U_{\hat{t}}} \\ &\leq \frac{1+A_{\hat{t}}}{\max(R_{\hat{t}},1)}\cdot \frac{V_{\hat{t}}}{1+U_{\hat{t}}} \leq \alpha \cdot \frac{V_{\hat{t}}}{1+U_{\hat{t}}} = \alpha \cdot (\frac{1+\mid \mathcal{C}_{\hat{t}}\mid}{1+U_{\hat{t}}}-1) \end{align*}\]

이제 \(\hat{FDP}_{\hat{t}}\)의 상한은 귀무가설 하의 p-value에 의존하는 \(U_{\hat{t}},V_{\hat{t}}\)에 의해서만 결정된다. 보조정리의 조건으로 \(\mathcal{C}_{\hat{t}}\)에 속하는 p-value들에 대해서는 가정에 의해 서로 독립이고 mirror conservative 조건에 의해 \(Pr(b_i = 1\mid\mathcal{G}_{-1}) \geq 0.5\)를 만족한다.

즉 $\rho = 0.5$로 잡을 수 있다. 즉 다음의 관계식이 만족한다.

\[\mathbb{E}[FDP|\mathcal{G}_{-1}] \leq \alpha \cdot (\mathbb{E}[\frac{1+ \mid\mathcal{C}_{\hat{t}}\mid}{1+U_{\hat{t}}}] -1) \leq \alpha \cdot(0.5^{-1}-1) = \alpha\]

이제 양변에 기댓값을 취하면, 총 기대의 법칙에 의해 $FDP \leq \alpha$를 만족한다.

정리하자면, AdaPT에서의 FDR 통제는 귀무가설 p-value들이 서로 상호 독립이고, 대립가설 p-value 집단과도 독립이어야 한다는 가정하에서 유한 표본에 대해서도 성립한다.

적절한 임계값의 설정

데이터의 분포를 완전히 안다고 가정할 때의 어떠한 임계값이 적절한지 보일 것이다. 여기서는 적절한 조건 하에서 two-groups model에 대한 베이즈 최적의 임계값은 local fdr의 등위면임을 보일 것이다.

The two-groups model과 local false discovery rate(lfdr)

서로 독립인 결합 확률분포 \((x_i,H_i,p_i) \in \mathcal{X}\times \{0,1\}\times [0,1] \ (i\in[n])\)에 대해 다음이 성립한다.

\[\begin{align*} H_i|x_i &\sim Ber(\pi_1(x_i)) \\ p_i|x_i &\sim (1-\pi_1(x_i)) \cdot 1 + \pi_1(x_i)f_1(p|x_i) \end{align*}\]

일반적으로 $f_0$에 대해서는 균등 분포를, $f_1$에 대해서는 귀무가설에 비해 더 작은 값을 갖도록 단조감소함수를 가정한다. 이 경우, 다음의 근사가 가능하다.

\[f(1|x) = 1-\pi_1(x) + \pi_1(x)f_1(1|x) \approx 1-\pi_1(x) + \pi_1(x) \cdot 0 = 1-\pi_1(x)\]

lfdr의 정의는 다음과 같다.

\[lfdr(p|x) = Pr(null|x,p) = \frac{1-\pi_1(x)}{f(p|x))} \approx \frac{f(1|x)}{f(p|x)}\]

자연스럽게 lfdr의 추정치는 데이터로부터 추정한 mixture $\hat{f}$를 사용하여, \(\hat{f}(1\mid x)/\hat{f}(p\mid x)\)를 이용한다. 이러한 추정량을 사용하는 이유는 주어진 데이터로부터 $\pi_1,f_1$을 식별해낼 수 없기 때문이다.

e.g. \(\pi_1 = 0.5, f_1(p\mid x) = 2(1-p)\)와 \(\pi_1 =1, f_1(p \mid x) =1.5(1-p)\)는 갖은 mixture \(f(p \mid x)\)를 갖는다.

Optimal threshold

주변 정보의 support $\mathcal{X}$에 대한 확률 측도 $\nu$라 하면, 확률변수 $X \sim \nu$를 이용하여, FDR과 검정력을 다음과 같이 쓸 수 있다.

\[\begin{align*} FDR(s,\nu) &= Pr(H=0|P \leq s(X)) \\ Pow(s,\nu) &= Pr(P \leq s(X)|H=1) \end{align*}\]

이제 네이만-피어슨과 같이 다음과 같은 최적화 문제를 고려하자.

\[\max_sPow(s,\nu) \text{ subject to } FDR(s,\nu) \leq \alpha\]

위 문제를 귀무 분포 $F_0$, 대립 분포 $F_1$로 나타내기 위해 다음과 같이 $Q_0,Q_1$을 정의하자.

\[\begin{align*} Q_0(s) &= Pr(P\leq s(X), H=0) = \int_{\mathcal{X}}F_0(s(x)|x)(1-\pi_1(x)) \nu(dx) \\ Q_1(s) &= Pr(P\leq s(X), H=1) = \int_{\mathcal{X}}F_1(s(x)|x)\pi_1(x) \nu(dx) \end{align*}\]

$Q_0,Q_1$을 이용해 최적화 문제를 아래와 같이 쓸 수 있다.

\[\max_s \frac{Q_1(s)}{Pr(H=1)} \text{ subject to } \frac{Q_0(s)}{Q_0(s)+Q_1(s)} \leq \alpha\] \[\min_s - Q_1(s) \text{ subject to } (1-\alpha)Q_0(s) - \alpha Q_1(s) \leq 0\]

이제 이를 strong duality를 갖는 convex optimization 문제로 바꿔서, KKT 조건을 이용하여 원문제와 라그랑주 함수를 이용한 쌍대문제의 최적해를 만족하는 관계식을 통해 최적의 임계값을 유도하려 한다.

따라서, 위 원문제를 strong duality를 갖는 convex optimization문제로 바꾸기 위해 다음을 만족해야한다.

Convexity and Slater’s Condition

• 원문제의 convexity: convexity의 경우, $Q_0,Q_1$의 이차 도함수가 0 이상임을 보이면 충분하고, 이는 \(f'_0(s(x) \mid x) \geq 0 , f'_1(s(x) \mid x) \leq0\) 즉, $f_0$은 연속인 단조 증가 함수, $f_1$은 연속인 단조 감소 함수여야 한다.
• Slater’s condition: $FDR(s,\nu) < \alpha$인 $s$가 최소 하나 이상 존재(strictly feasible)해야 한다. 이에 대한 조건은 $\nu$가 ${x_i}$에서 support를 갖고, \(\nu(\{x_i: f(0 \mid x_i) >0, lfdr(0 \mid x_i) < \alpha\})\} > 0\)을 만족하는 이산인 확률 측도여야 한다.

위 두 조건을 만족하면, strong duality를 만족한다.

첫번째 조건에 대해서는 일반적으로 귀무 분포의 경우 균등 분포를, 대립 분포의 경우 매우작은 p-value를 갖는 연속이 분포를 고려하는 것이 자연스럽기에 대부분의 경우 성립한다.

두번째 조건을 만족하지 않는다면, local FDR이 대부분의 경우에서 $\alpha$를 넘음을 의미함으로, 어떠한 임계점을 찾는 규칙도 FDR을 $\alpha$이하로 통제할 수 없음으로 마찬가지로 자연스럽다.

이제 원문제에 대한 라그랑주 함수는 아래와 같다.

\[L(s;\lambda) = \int_{\mathcal{X}}[-(1+\lambda\alpha)F_1(s(x)|x)\pi_1(x) + \lambda(1-\alpha)F_0(s(x)|x)(1-\pi_1(x))]\nu(dx)\]

따라서, KKT 조건을 만족하기 위해 stationarity 조건에 대해서 풀면, 최적 임계점 $s^*(x)$는 아래의 관계식을 만족한다.

\[(1+\lambda\alpha)f_1(s^*(x)|x)\pi_1(x) = \lambda(1-\alpha)f_0(s^*(x)|x)(1-\pi_1(x))\] \[f(s^*(x)|x) = f_0(s^*(x)|x)(1-\pi_1(x)) + \frac{\lambda(1-\alpha)}{1+\lambda \alpha}f_0(s^*(x)|x)(1-\pi_1(x))\] \[(1+\frac{\lambda(1-\alpha)}{1+\lambda \alpha})^{-1} = lfdr(s^*(x)|x)\] \[lfdr(s^*(x)|x) = \frac{1+\lambda\alpha}{1+\lambda}\]

다시 말해서, 최적 임계점 $s^*(x)$는 lfdr이 $(1+\lambda \alpha)/(1+\lambda)$가 되는 등위면이다.

또한, KKT조건에서의 complementary slackness에 의해, $FDR(s^*,\nu) = \alpha$를 만족해야 한다. 다시말해서, 최적의 임계값은 FDR이 $\alpha$가 되는 지점이다.

실제 분석시에는, \(lfdr(p \mid x)\)의 추정량인 \(\hat{f}(1 \mid x)/\hat{f}(p \mid x)\)에 대한 등위면에 해당하는 $s^*$들을 최적의 임계값으로 사용한다. 이제, 데이터로부터 mixture density $\hat{f}$를 추정해야 한다.

Density estimation

$\pi_1(x), f_1(p|x)$를 GLM을 통해 각각 모수 $\theta, \beta$를 이용하여 가정하여 가능도를 최대화하는 $\hat{\theta}, \hat{\beta}$를 추정한다. $\pi_1, f_1$ 각각에 대한 전처리 함수를 $\phi_{\pi}, \phi_{\mu}$라고 하자.

\[\begin{align*} H_i|x_i &\sim Ber(\pi_i), \ \log(\frac{\pi_1(x_i)}{1-\pi_1(x_i)}) = \theta^T\phi_{\pi}(x_i) \\ f(p|x_i,H_i) &= 1^{1-H_i}\cdot \exp(\eta_i^TT(p) - A(\eta_i)+S(p))^{H_i}, \ \mu_i = A'(\beta^T\phi_{\mu}(x_i)) \end{align*}\]

전체 로그 가능도는 다음과 같다.

\[\begin{align*} l(\theta,\beta;p,H,x) &= \log \prod_{i=1}^n[Pr(H_i|x_i)\cdot Pr(p_i|H_i,x_i) ]\\ &= \ \sum_{i=1}^n[(1-H_i)\log(1-\pi_1(x_i)) + H_i\log \pi_1(x_i) + H_i(\eta_i^TT(p) - A(\eta_i) + S(p))] \end{align*}\]

AdaPT에서는 매 스텝마다 가려진 p-value들이 존재함으로 전체 가능도를 알 수 없기에, EM알고리즘을 사용하여 $(\hat{\theta}, \hat{\beta})$를 구하고, 이를 통해 mixture density $\hat{f}$를 추정한다.

Extension to dependent data using knockoffs

AdaPT는 유한 표본에 대해서 p-value의 독립성 가정이 깨지면, FDR 통제를 보장하지 못한다. 특히, 독립이 아닌 p-value 데이터를 이용해 AdaPT를 수행하면, 국소적인 임의의 상관관계를 유의미한 신호로 착각하여 잘못된 발견을 하는, 과적합의 위험이 있다. (즉, $\hat{FDP}_t$가 과소 추정된다는 편향이 발생하여, FDR 통제가 실패할 수 있다.)

이 경우에 p-value가 회귀 계수나 다변량 정규분포를 따르는 검정통계량으로부터 계산되었고, 원본 데이터셋 $(X,y)$에 접근할 수 있는 경우, Knockoff+ 절차를 결합하여 p-value의 종속성 문제를 해결할 수 있다.

knockoff+ filters

독립변수 $X \in \mathbb{R}^{n \times d}$와 종속변수 $y \sim \mathcal{N}_n(X\beta, \sigma^2I_n)$을 통해, 귀무가설 $H_j: \beta_j=0, j=1,…,d$를 검정하는 다중 검정을 고려하자.

독립 변수에 대해 다음을 만족하는 가짜 데이터 $\tilde{X} \in \mathbb{R}^{n \times d}$를 계산한다. ( $n \geq 2d$이고 $X$가 full-column rank를 만족하면 이러한 $\tilde{X}$의 존재성을 보장할 수 있음이 알려져 있다.)

1. $\hat{\Sigma} = X^TX = \tilde{X}^T\tilde{X}$
2. $\tilde{X}^TX = X^TX -D$를 만족하는 대각행렬 $D= diag(d_j)(d_j>0, \ \forall j=1,…,d)$가 존재한다. 다시말해서, $Cov(\tilde{X}_i, X_i) < Var(X_i), \forall i$를 만족한다.

이제 독립변수간의 상관관계가 동일한 가짜 데이터를 만들었음으로, 독립변수간 상관관계 속에서 특정 변수가 선택된 것이 실제 효과 때문인지, 아니면 단순히 다른 중요한 변수와의 상관관계 때문인지를 $X,\tilde{X}$ 각각을 종속변수 $y$간의 선형관계를 비교하여 비교할 수 있다.

이제 실제 변수와 가짜변수에 대해 종속변수와의 선형관계를 나타내는 통계량 $v= X^Ty, \tilde{v} = \tilde{X}^Ty$를 정의하면, $(v_j)_{j \notin \mathcal{H}_0}$을 조건부로 한 귀무가설에 대응하는 \(((v_j, \tilde{v}_j))_{j \in \mathcal{H}_0}\)는 독립이고 교환 가능한 쌍이다. (선형관계가 없는 변수들임으로 진짜와 가짜의 차이가 없다.)

knockoff filter는 이를 이용하여 실제 변수와 가짜 변수의 차이를 나타내는 knockoff 통계량 $w(X,y) \in \mathbb{R}^d$를 정의한다.

1. 이산형 p-value

$w_j$의 크기를 부가정보 $x_j$로 사용하고, $w_j$의 부호를 이용해 성공확률이 0.5인 이산형 p-value $b_j$를 생성하면 이는 mirror conservative 조건을 만족하기에, $(x_j, b_j)$를 AdaPT에 적용한다.

자세한 과정은 아래와 같다.

시그마필드 \(\mathcal{F}_{-1} = \sigma(\{v_j, \tilde{v}_j\}_{j=1}^d)\)를 정의한다. 다음 조건을 만족하도록 knockoff 통계량을 정의한다.

1. Sufficiency Condition: $|w_j|$는 \(\{v_j,\tilde{v}_j\}\)쌍의 순서를 몰라도 계산이 가능해야 한다. 즉 \(\mathcal{F}_{-1}\)에서 측정가능해야 한다. 따라서 부가정보로 사용할 수 있다.
2. Antisymmetry Condition: $w_j = w(v_j, \tilde{v}_j) = -w(\tilde{v}_j, v_j), \ \forall j$. 귀무가설 하에서 $(v_j, \tilde{v}_j)$는 교환가능함으로, $w_j$는 0을 기준으로 대칭인 분포를 갖기에, $Pr(w_j>0) = 0.5$가 된다. 귀무가설 하의 $b_j = 1-sgn(w_j)$ 는 서로 독립이고 성공확률이 0.5인 베르누이 시행을 따른다.

이산형 p-value $b_j$의 경우, $\min(b_j,1-b_j)$는 항상 0이기에 임계점과 비교하는 방식은 의미가 없다.

이 경우에는, 전체 가설을 후보 기각집합에 포함하여, \(\hat{FDP}_t \leq \alpha\)를 만족할 때 까지, 매 반복마다 남아있는 후보 기각집합에서 $|w_j|$ 가 가장 작은 가설들을 하나씩 제거한다.

2. 연속형 p-value

만약 $\sigma^2$이 알려진 경우, $(v,\tilde{v})$를 이용하여 다음의 결합확률분포의 관계가 성립한다.

\[(v+\tilde{v}, v-\tilde{v})^T \sim \mathcal{N}_{2d}\left(\mu_{v,\tilde{v}}, \sigma^2\Sigma_{v,\tilde{v}} \right) \text{ where } \Sigma_{v,\tilde{v}} = diag(4X^TX-2D,2D)\]

이제, $v- \tilde{v}$의 주변부 분포를 이용해 $H_j:\beta_j=0$의 양측검정 p-value를 구할 수 있다.

\[z_j = \frac{v_j-\tilde{v}_j - 2\beta_j}{\sqrt{2d_j\sigma^2}} \sim \mathcal{N}(0,1), \ p_j = 2\min(\Phi(z_j), 1- \Phi(z_j))\]

IHW

Ignatiadis, N. & Huber, W. (2021). Covariate powered cross-weighted multiple testing.

다중검정에서 일부 가설들은 다른 가설들에 비해 귀무가설이 참일 사전확률이 높거나 검정력이 차이가 있을 수 있고, 이를 hypothesis heterogeneity라고 한다. IHW에서는 가중치를 이러한 heterogeneity를 나타낼 수 있는 벡터 $X_i$에 대한 함수로 나타낸다.

${(X_i, P_i)\in \mathcal{X} \times [0,1]}_{i=1}^n$을 $K$개의 폴드로 나눠서 각각의 부분을 $I_l,l=1,…,K$로 나타낸다.

폴드 $I_l$에 속하는 $(X_i,P_i)$에 대해서는 $\hat{W}^{-l}: \mathcal{X}\rightarrow \mathbb{R}^+$의 가중치 함수와 마찬가지로 데이터로부터 학습되는 임계점 $\hat{t}$를 이용하여 다음을 만족하는 가설들을 기각한다.

\[P_i \leq \hat{t} \cdot \hat{W}^{-l}(X_i)\]

$\hat{W}^{-l}$는 데이터로 부터 학습되며, $I_l$에 속하는 샘플들을 제외한 나머지 $K-1$개의 폴드에 속한 샘플들로부터 학습한 함수임을 의미한다. 이러한 학습방법을 교차 가중(cross-weighting)이라고 부른다.

Weighted and cross-weighted multiple testing

Genovese, Roeder, and Wasserman(2006)에서 제안한 가중치는 사전에 정하여 고정된 값으로, 데이터와 무관한 결정론적인 가중치인 반면 IHW는 데이터로부터 학습된 가중치를 사용한다.

가중치를 데이터로부터 학습할 때, 우연히 작게 나온 귀무 p-값들이 서로의 가중치를 부풀려 전체 기각 수를 늘리는 적대적 공조(adversarial coordination)가 발생할 수 있다. 이를 방지하기 위해, 다음과 같이 고정된 $\tau$를 정의하여 $\tau$-censored wBH절차를 사용한다.

\[P_i \leq \min\{w_i \cdot \hat{t}, \tau\}, \ \tau \in (0,1]\]

즉, 기각되는 가설의 수는 $\tau$가 감소할수록 마찬가지로 감소한다. 이전 논의에서의 wBH절차들은 $\tau=1$로 가려짐이 발생하지 않는, 특별한 경우로 볼 수 있다.

또한 이산인 공변량의 예시를 통해 교차 가중의 필요성을 보일 수 있다. $X_i \in {1,…,G}$라면 각 그룹 $g$마다 귀무가설 비의 추정량 $\hat{\pi}_0(g)$를 구하여 $(1-\hat{\pi}_0(g))/\hat{\pi}_0(g)$를 정규화한 가중치를 사용하여 wBH절차를 수행할 수 있다.(GBH, Hu et al. 2010)

귀무가설 비의 추정량은 Storey의 추정과 같이 아래의 관계식을 이용한다.

\[\begin{align*} Pr(P_i > \tau |X_i=g) &= \pi_0(g) \cdot (1-\tau) + (1-\pi_0(g))\cdot Pr(P_i > \tau|H_i=1)\\ &\approx \pi_0(g) \cdot (1-\tau) \\ Pr(P_i> \tau|X_i=g) &= \mathbb{E}[I(P_i >\tau|X_i=g)] \approx \frac{\sum_{i:X_i=g }I(P_i > \tau)}{|\{i:X_i=g\}|} \end{align*}\]

따라서, 다음과 같은 추정량을 사용한다.

\[\hat{\pi}_0(g)= \frac{\sum_{i:X_i=g }I(P_i > \tau)}{|\{i:X_i=g\}|(1-\tau)}\]

이제 naive GBH와 교차 가중을 활용한 IHW-GBH 절차의 알고리즘은 다음과 같이 쓸 수 있다.

전역 귀무가설(global null) 가정한 상황, 즉 10,000개의 $p_i$가 독립인 균등분포를 가정하여 각 샘플의 인덱스 $i$를 이용하여, $X_i = i \text{ mod }G$를 통해 공변량을 계산하여, $\alpha=0.2, \tau = 0.5$로 설정하여 $G$를 조절해가면서 각각마다 총 12,000번의 몬테카를로 시뮬레이션을 반복하여 FDR을 평균내어 계산하였다. 즉, $G$가 클 수록 각 그룹에 속하는 샘플의 수는 줄어들고 과적합의 위험이 있다.

모든 가설이 귀무가설이므로 이상적인 다중검정 절차라면 FDR이 $\alpha=0.2$를 초과해서는 안되지만 아래와 같이 GBH의 경우 그룹 내 샘플수가 줄어들면서 무작위적인 p-값의 분포차를 과적합하여 FDR이 $\alpha$를 초과함을 알 수 있다.

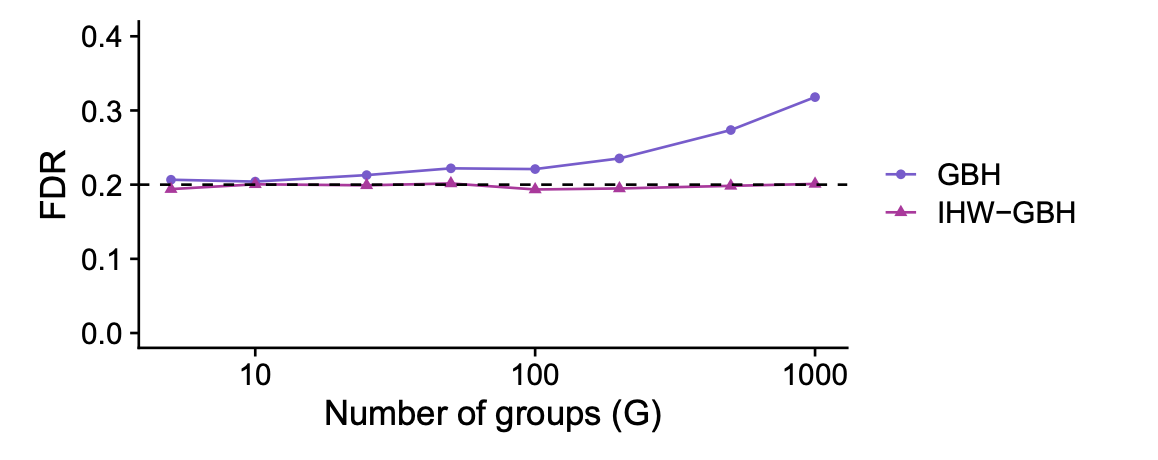
Finite-sample FDR control with cross-weighting under independence

p-value와 부가정보 쌍 ${(P_i,X_i):i\in [n]}$에 대해 다음이 성립한다고 가정하자.

1. \(\{(P_i,X_i)\}_{i \in \mathcal{H}_0}\)은 서로 독립이며, \(\{(P_i,X_i)\}_{i \notin \mathcal{H}_0}\)과 독립이다.
2. 귀무가설 하에서 $P_i$와 $X_i$는 서로 독립이다.
3. (conservativeness) 귀무가설 하에서 \(Pr(P_i \leq t) \leq t, \ \forall t\in[0,1]\)

AdaPT에서와 같이 $X_i$를 주변화하거나 상수로 봐서 조건 1,2를 $P_i$에만 국한하여 논의를 이어나갈 수도 있다. 중요한 점은 조건 2에서와 같이 귀무분포에서 부가정보는 p-value와 독립이어야 한다.

이제 가중치에 대해 다음의 조건을 정직한 가중치(Honest weighting)이라고 한다.

$I_1\cup…\cup I_K = [n] , \ I_i \cap I_j = \emptyset \ \forall i\neq j$를 만족하는 폴드 ${I_l}$에 대해 $I_l^c = [n]-I_l$이라고 하자. 데이터로부터 획득된 가중치 ${W_i}_{i \in [n]}$이 다음을 만족할 때 폴드 ${I_l}$에 대한 정직한 가중치라고 한다.

1. 임의의 $i \in I_l$에 대한 $W_i$는 \(\{P_j\}_{j \in I_l^c}\)와 \(\{X_j\}_{j \in [n]}\)에 대한 함수이다. 즉, 같은 폴드에 속한 p-value들의 영향을 받지 않는다.
2. 각각의 폴드에 속하는 가중치의 평균은 1이다. 즉, $\sum_{i \in I_l}W_i = |I_l|, \ \forall l$. 이는 Genovese에서의 $\sum_iW_i=m$ 조건을 만족하고, 폴드 간의 정보 유출을 막기 위해 각 폴드마다의 평균으로 제한하였다.
3. $W_i$는 음이 아니다.

또한 가중치 $W_i$가 접근할 수 있는 p-value가 $P_iI(P_i>\tau)$일 경우, $\tau \in (0,1]$에 대해 $\tau$-censored라고 한다.

위의 조건을 모두 만족하는 IHW-BH 절차는 유한한 샘플에 대해서 \(FDR \leq \alpha \mathbb{E}[\sum_{i\in \mathcal{H}_0}W_i]/n\)을 만족한다. 이는 주어진 $\alpha$에 귀무가설 비 $\pi_{0W} =\mathbb{E}[\sum_{i\in \mathcal{H}_0}W_i]/n$가 곱해져서 불필요하게 보수적인 통제이다.

Storey의 null-proportion adaptive methods를 참고하여, 아래와 같이 $\pi_{0W}$의 추정량을 폴드마다 구하여, $W_i^{\text{Storey}}=W_i/\hat{\pi}_{0Wl}$을 사용한 IHW 절차도 FDR을 $\alpha$이하로 통제함을 보일 수 있다. 이를 HW-Storey 절차라고 한다.

\[\hat{\pi}_{0Wl} = \frac{\max_{i \in I_l}W_i + \sum_{i \in I_l}W_iI(P_i > \tau')}{|I_l|(1-\tau')} \text{ with } \tau' \in (\tau,1]\]

IHW에서는 일반적으로 $\tau’=0.5$를 선택할 것을 제안한다.

Learning powerful weighting rules

AdaPT에서와같은 two-groups model을 가정하자.

\[\begin{align*} X_i &\sim \nu, \ H_i|X_i=x \sim Ber(1-\pi_0(x))) \\ P_i|X_i=x &\sim F(\cdot|x)=\pi_0(x)U + (1-\pi_0(x))F_{alt}(\cdot|x) \end{align*}\]

이제 부가정보를 활용한 임계값 $s:\mathcal{X} \rightarrow [0,1]$함수를 통해 $P_i \leq s(X_i)$를 만족하는 가설을 기각한다. 임계값 함수는 다음을 만족하는 최적화 문제이다.

1. \[mFDR(s) = Pr(H_i=0 \mid P_i \leq s(X_i)) \leq \alpha\]
2. 기각하는 가설의 총개수의 기댓값 \(\mathbb{E}[\sum_i I(P_i \leq s(X_i))] = \sum_i F(s(X_i) \mid X_i)\)가 최대가 되어야 한다. 즉, 검정력을 최대화하는 문제이다.

또한 mFDR에 대해 다음이 만족한다.

\[\begin{align*} mFDR(s) &= Pr(H_i=0|P_i \leq s(X_i)) \\ &=\frac{Pr(H_i=0, P_i\leq s(X_i)}{Pr(P_i \leq s(X_i))} \\ &= \frac{\mathbb{E}[ Pr(P_i\leq s(X_i)|H_i=0,X_i) \cdot Pr(H_i=0,X_i)]}{\mathbb{E}[Pr(P_i \leq s(X_i))|X_i]} \\ &= \frac{\mathbb{E}[s(X_i)\pi_0(X_i)]}{\mathbb{E}[F(s(X_i)|X_i]} \end{align*}\]

따라서 조건 1을 \(\mathbb{E}[s(X_i)\pi_0(X_i)] \leq \alpha \mathbb{E}[F(s(X_i) \mid X_i]\)로 다시 쓸 수 있다.

이제 이를 교차-가중(cross-weighting)을 고려하여 각 폴드마다의 문제로 분리하여 푼다. 즉, 각 폴드 $l$마다의 임계함수는$\hat{s}^{-l}$를 학습해야 한다.

먼저 각 폴드마다 $\hat{F}^{-l}(t|x), \hat{\pi_0}^{-l}(x)$를 데이터로부터 학습하여, 다음의 최적화 문제를 고려한다. 이제 임계점 함수는 각 폴드마다 다음을 최적화 하는 벡터 ${t_i}$로 주어진다. ($\hat{\pi_0}^{-l}(x)$의 추정없이 단순히 1로 고정하여도 많은 경우에 좋은 성능을 보인다.)

\[\max_{\{t_i\}_{i \in I_l} }\sum_{i \in I_l} \hat{F}^{-l}(t_i|X_i) \text{ subsetject to } \sum_{i \in I_l}\hat{\pi_0}^{-l}(X_i)t_i \leq \alpha \sum_{i \in I_l} \hat{F}^{-l}(t_i|X_i)\]

이제 아래와 같이 임계점 ${t_i}$를 정규화를 통해 가중치 ${W_i}$로 변환할 수 있다. 이는 각 폴드 내에서 가중치의 합이 가설의 수와 같아지도록 하여 정직한 가중치 조건을 만족할 수 있도록 한다.

\[W_i = \frac{|I_l| \cdot t_i}{\sum_{j \in I_l}t_j}, \ \forall i \in I_l, \ \forall l=1,...,K\]

만약 $\sum_{j \in I_l}t_j=0$인 폴드에 속하는 가중치에 대해서는 $W_i=1$로 고정한다.

만약 $\hat{F}^{-l}$가 오목함수라면 이는 convex optimization임으로 쉽게 풀 수 있다. 오목성을 보장하는 추정방법으로 그레난더 추정량(Grenander estimator)을 사용해 볼 수 있다. 공변량 $X_i$가 연속형인 경우에는 이산화 또는 그룹화(binning)한 뒤 각 그룹에 대해 그레난더 추정량을 구해볼 수 있다. 다만 그레난더 추정량은 비모수적 방법으로 ${P_i}_{i \in I_l}$을 정확히 알고 있어야 추정이 가능하다. 따라서 $\tau$-censored 가중치를 만들 수 없지만, 실험적을 좋은 성능을 보임이 밝혀져 있다. 또한 점근적 분석을 통해 표본의 수가 충분히 클 경우 $\tau$-censored 없이도 FDR통제가 가능함을 보일 수 있다. 이에 대한 대안으로는 AdaPT에서와 같이 EM 알고리즘을 이용하여 cdf를 추정해볼 수 있다.