저번 포스팅에 이어 이번에는 wBH절차 하에서 가설의 수가 충분히 많은 경우에 대해 데이터에만 의존하는 FDR의 상한을 유도해보자. 먼저, 확률변수의 수렴에 대해 복습해보자.
Genovese, C. R., Roeder, K., & Wasserman, L. (2006) False Discovery Control With P-Value Weighting
Roquain, E. & van de Wiel, M. A. (2009) Optimal weighting for false discovery rate control
의 내용을 참고하였다.
Convergence in probability v.s. Convergence almost surely
확률변수 열 $X_1,…,X_n$과 확률변수 $Z$에 대해 다음을 만족하면, 확률변수 열$X_n$은 확률변수$Z$로 확률수렴한다.
\[\lim_{n \rightarrow \infty}Pr(|X_n-Z| \geq \epsilon) = 0, \ \forall \epsilon >0\]$X_n \xrightarrow{p} Z$라고 표기한다.
이번엔 다음과 같이 극한이 확률 함수 내부로 들어가서, 다음을 만족하면 확률변수 열$X_n$은 확률변수$Z$로 거의 확실하게 수렴한다.
\[Pr(\lim_{n \rightarrow \infty}X_n=Z) = 1\]$X_n \xrightarrow{a.s.} Z$라고 표기한다. 확률 함수 내부의 집합을 표본공간 $\Omega$를 이용하여 아래와 같이 쓴다.
\[C=\{w \in \Omega : \lim_{n \rightarrow \infty} X_n(w) = Z(w)\}\]확률변수는 결국 표본공간 에서 실수를 매핑해주는 함수이므로, 이는 $X_n$이 $Z$로 수렴하는 모든 결과 $w$들을 모아놓은 집합이고 converges almost surely라는 것은 결국 이러한 집합의 확률이 $1$이라는 것이다. 반대로, 수렴하지 않는 예외적인 결과들의 집합의 확률이 $0$이다.
$C$는 잘 정의된 사건인가? 즉, 집합 $C$가 확률을 매길 수 있는 사건인지 확인해보자.
$\lim_{n \rightarrow \infty} X_n(w) = Z(w)$가 성립한다는 것은 엡실론-델타 논법과, 아르키메데스 성질에 의해 다음을 만족한다는 것과 같다.
\[\forall k \in \mathbb{N}, \ \exists K \in \mathbb{N} \ s.t. \ \forall n\geq K, \ |X_n(w) - Z(w)| \leq \frac{1}{k}\]먼저, 가장 내부의 집합을 아래와 같이 $A_{n,k}$로 나타내면 이는 자명하게 사건이다.
\[A_{n,k} = \{w: |X_n(w)-Z(w)| \leq \frac{1}{k}\}\]즉, $C$는 사건들의 가산 합집합과 교집합의 형태로 다음과 같이 나타낼 수 있으므로, 잘 정의된 사건이다.
\[C = \cap_{k=1}^{\infty}(\cup_{n=1}^{\infty}(\cap_{n=K}^{\infty}A_{n,k}))\]거의 확실한 수렴의 성질
거의 확실한 수렴이면 확률수렴한다.
거의 확실한 수렴이 더 강한 조건이다. 즉, $X_n \xrightarrow{a.s.} Z$이면, $X_n \xrightarrow{p} Z$이다. 이를 보이기 위해 다음과 같은 사건열 $B_n$을 고려해보자.
\[B_n = \cup_{m=n}^{\infty}\{|X_m-Z| > \epsilon \}\]사건열 $B_n$은 포함관계가 작아지는 사건들이기에, 사건의 극한을 정의할 수 있고, $w$가 모든 $B_n$에 속한다는 말은 $m$이 아무리 커도 $X_m(w)$가 $Z(w)$ 근방을 벗어난다는 말이다. 즉 $C$의 여사건임을 알 수 있다.
\[\lim_{n \rightarrow \infty}B_n = \cap_{n=1}^{\infty}B_n = \{w \in \Omega: \lim_{m \rightarrow \infty}X_m(w)\neq Z(w)\}=C^c\]$X_n \xrightarrow{a.s.} Z$임을 가정하면, 이러한 사건의 극한의 확률값은 $0$임을 알 수 있다. 또한 확률측도의 연속성에 의해 다음이 성립한다.
\[\begin{align*} 0&=Pr(\lim_{n \rightarrow \infty}B_n) = \lim_{n \rightarrow \infty}Pr(B_n) \\&=\lim_{n \rightarrow \infty}Pr( \cup_{m=n}^{\infty}\{|X_m-Z| > \epsilon \}) \geq \lim_{n \rightarrow \infty}Pr( |X_n-Z| > \epsilon) \geq 0 \end{align*}\]따라서 $X_n \xrightarrow{p} Z$이다.
연속성 사상 정리 (The continuous mapping theorem, CMT)
거의 확실한 수렴에 대해서도 연속성 사상정리가 성립한다. 즉, 연속함수 $g$에 대해 $X_n \xrightarrow{a.s.} Z$이면 $g(X_n) \xrightarrow{a.s.} g(Z)$
지배 수렴 정리(The Dominated Convergence Theorem, DCT)
- $X_n \xrightarrow{a.s.} Z$ (수렴조건)
- $Y_n = |X_n-Z|$에 대해 항상 크거나 같은 값을 갖는 확률변수 $W$가 존재하고, $W$의 기댓값이 존재한다. (지배조건)
위 두 조건을 만족하면, 아래와 같이 적분과 극한의 순서를 바꿀 수 있다.
\[\lim_{n\rightarrow \infty}\mathbb{E}[|X_n-Z|] = \mathbb{E}[\lim_{n\rightarrow \infty}|X_n-Z|] =0\]FDR의 상한 (가설의 수가 충분히 큰 경우)
이후 논의에서는 wBH 절차의 임계점을 $T_{m}$이라고 표기하자.
\[T_{m} = \sup\{t:\hat{C}_m(t)\geq \frac{1}{\alpha} \} \text{ where } \hat{C}_m(t) = \frac{\hat{D}_m(t)}{t\bar{W}_m} = \frac{\sum_{i}I(P_i\leq W_it)}{t\sum_iW_i}\]$\hat{C}_m(t)$는 $Q$의 주변부 cdf $D$와 $W_i$의 기댓값 $\mu$의 추정량을 사용한 함수이므로, 점근분석을 위해 다음을 고려해보자.
\[t_* = \sup\{t:C(t)\geq \frac{1}{\alpha} \} \text{ where } C(t) = \frac{D(t)}{t\mu}\]Note. 이전 포스팅에서 $D(t) = (1-a) \mu_0 t+ a \int F(wt)dQ_1(w)$임을 보였다.
만약 대립가설 하에서의 $P_i$의 조건부 cdf $F$가 support $[0,1]$에서 순오목함수라면, 즉 다음을 만족한다고 가정하자.
\[F(\lambda x + (1-\lambda) y)>\lambda F(x) + (1-\lambda)F(y), \ \forall \lambda, x,y\in[0,1]\]이러한 경우 $P_i$의 주변부 cdf $G = (1-a)U + aF$는 마찬가지로 $[0,1]$에서 순오목 함수이며, $Q$의 주변부 cdf $D$ 또한 $Q_1$의 support가 $(0,\infty)$이기에, $[0,1]$에서 적분항 내부에 $F(w(\lambda x + (1-\lambda) y))$가 $\lambda F(wx) + (1-\lambda)F(wy)$보다 항상 크기에 동일한 구간에 대해 적분한 결과도 항상 크다. 따라서 $D$도 $[0,1]$에서 순오목 함수이다.
또한 $D(0)=0$이며, $0<t_0<t_1<1$에 대해 $\lambda = t_0/t_1$을 대입하면 $t_0 = (1-\lambda)+\lambda t_1$이다. 즉, 다음과 같이 $C(t)$는 $(0,1)$에서 단조 감소함수이다.
\[C(t_1) = \frac{D(t_1)}{t_1} = \frac{(1-\lambda)D(0)+\lambda D(t_1)}{t_0} < \frac{D(t_0)}{t_0} = C(t_0)\]만약 $F$가 $[0,1]$에서 순오목함수라면, $T_m \xrightarrow{a.s.} t_*$이며, FDR은 $\alpha +o(1)$보다 작거나 같다. 이제 이를 보이려 한다.
증명 과정은 대략 $T_m \xrightarrow{a.s.} t_*$임을 보이고, 이를 이용하여 \(FDR(T_m ) \xrightarrow{a.s.} FDR(t_*)\)임을 확인하여, 지배수렴정리를 사용해 FDR이 어떤 값으로 수렴하고, 이 수렴값이 \(\alpha + o(1)\)임을 보인다.
1. $T_m$에서 $t_*$로의 거의 확실한 수렴
먼저, $\sum_iW_i=m$인 제약조건이 없는 서로 독립인 경우를 생각해보자. 양수 $b,\epsilon$ 를 고정하여 $T_m$이 \((t_*-b, t_*+b)\)에 갇힘을 통해 수렴성을 보이려 한다.
다음은 증명없이 사용한다.
- (글리벤코-칸텔리 정리) $Q_i$는 서로 독립임으로, 주변부 cdf $D$와 이에 대한 emprical cdf $\hat{D}_m$에 대하여 충분히 큰 $m$에 대해 다음이 성립한다. ($m$이 충분히 크면 경험적 cdf는 cdf로 거의 확실하게 균등수렴한다.)
- (대수의 강법칙) $\bar{W}_m \xrightarrow{a.s.} \mu$
Note. $n$개의 iid인 확률변수열 $X_i \sim F$에 대해 supprot상의 $x$를 고정하면 empirical cdf는 $I(X_i\leq x)$의 표본평균이기에 대수의 강법칙에 의하면 $n$이 충분히 크면, $\mathbb{E}[I(X_1\leq x)] = Pr(X_1 \leq x) = F(x)$로 거의 확실하게 수렴한다. 즉, $x$마다의 점별수렴을 의미한다. 하지만, 글리벤코-칸텔리 정리는 이보다 더 강한 모든 support상의 $x$에 대한 균등한 수렴을 보장한다.
$C$는 단조 감소임으로, \(C(t_*+b) = 1/\alpha - \delta\) ( $\delta >0$ )이다. 따라서 $t>t_*+b$인 경우의 위 두 정리를 사용하면 다음의 부등식이 성립한다.
\[\begin{align*}\hat{C}_m(t) &= \frac{\hat{D}_m(t)}{t\bar{W}_m} \leq \frac{D(t) + \sup_u |\hat{D}_m(u) - D(u)|}{t\mu -t|\bar{W}_m-\mu|} \\ &\leq \frac{D(t) +\epsilon}{t\mu-t\epsilon} = C(t)(\frac{\mu}{\mu-\epsilon}) + \frac{\epsilon}{t(\mu-\epsilon)} \\ &\leq (\frac{1}{\alpha}-\delta)(\frac{\mu}{\mu-\epsilon}) + \frac{\epsilon}{(t_*+b)(\mu-\epsilon)} < \frac{1}{\alpha} \end{align*}\]한편, $\hat{C}(T_m) \geq 1/\alpha$임으로, $T_m \leq t_*+b$이다.
마찬가지로, \(t < t_*-b\)인 경우에 대해서는 \(C(t_*-b) = 1/\alpha +\delta\) ( \(\delta >0\) )임으로, \(\hat{C}_m(t) > 1/\alpha\)이다. 한편, $T_m$은 이러한 $t$들의 상한임으로 \(T_m \geq t_*-b\)여야 한다. 따라서, $T_m \xrightarrow{a.s.} t_*$이다.
2. $FDP(T_m)$에서 $FDP(t_*)$로의 거의 확실한 수렴
이제, $FDP(T_m)$이 $FDP(t_*)$로 거의 확실하게 수렴함을 보여보자.
\[FDP(T_m) = \frac{\sum_{i}I(Q_i \leq T_{m})(1-H_i)/m}{\sum_iI(Q_i\leq T_{m})/m} = \frac{\hat{V}_m(T_m)}{\hat{D}_m(T_m)}\]충분히 큰 $m$에 대해 \(\hat{V}(T_m), \hat{D}_m(T_m)\)이 각각 \(V(t_*), D(t_*)\)로 확실하게 수렴함을 보이면, $x/y$는 연속함수이기에 $FDP(t_*)$로 거의 확실하게 수렴한다. 두가지 모두 증명의 방식은 동일하기에 분모의 경우만 보여보자.
\[|\hat{D}_m(T_m) - D(t_*)| \leq \sup_u |\hat{D}_m(u) - D(u)| + |D(T_m) - D(t_*)| \rightarrow 0\]오른쪽 항의 첫번째 항은 글리벤코-칸텔리 정리에 의해 $0$으로 수렴하고, \(T_m \xrightarrow{a.s.} t_*\)이고 $D$는 순오목 함수이므로, 연속함수이다. 따라서 연속성 사상정리에 의해 $D(T_m) \xrightarrow{a.s.} D(t_*)$임으로, 위는 $0$으로 수렴한다.
또한, $FDP$는 항상 $0,1$사이의 값을 갖으므로(지배조건을 만족), 지배수렴정리에 의해 다음이 성립한다.
\[\begin{align*} &|\mathbb{E}[FDP(T_m)] - \mathbb{E}[FDP(t_*)]| \le \mathbb{E}[|FDP(T_m)-FDP(t_*)|] \rightarrow 0 \end{align*}\]즉, FDR은 $\mathbb{E}[FDP(t_*)]$로 수렴한다. 또한 수렴값의 상한은 아래와 같다.
\[\mathbb{E}[FDP(t_*)] = \frac{\mathbb{E}[(1-H_i)I(Q_i\leq t_*)]}{\mathbb{E}[\hat{D}(t_*)]} = \frac{(1-a)\mu_0t_*}{t_*\mu/\alpha} \leq \alpha\](위 부등식은 $\mu = (1-a)\mu_0+a\mu_1$이고, $W$의 support는 음이 아니기에 성립한다.)
따라서, $FDR \leq \alpha + o(1)$임을 알 수 있다.
Power arbitrage
wBH절차의 검정력에 대해 알아보자. 가중치를 부여하는게 BH절차에 비해 효과적이려면, 가중치가 잘 부여되었을 때에는 검정력이 상승하고, 잘못 부여되었을 때에는 너무 낮게 떨어지지 않아야 한다. 결론부터 말하면, 가중치를 잘 사용하면 검정력이 크게 향상되는 반면, 가중치를 잘못 사용하더라도 검정력의 손실은 크지 않다. 이를 Power arbitrage라고 부른다. $\mu = (1-a)\mu_0 + a\mu_1 = 1$인 상황을 가정한다. 즉, $0<\mu_0 <1/(1-a)$이고, $0<\mu_1<1/a$이다.
$\mu_1>1$인 경우를 유익한 경우(Informative case), $\mu_1<1$인 경우를 잘못된 경우(mis-Informative case) 로 나눠 분석을 진행한다.
mis-Informative case
먼저, mis-Informative인 경우의 손실이 작은 이유는 모델 가정에 있어서 대립가설의 분포가 항상 귀무가설 하에서보다 작은 확률분포를 가정하였기 때문이다.
- 실제 대립가설에 실수로 낮은 가중치를 부여하더라도, 대립가설에서 나온 p-value가 충분히 작기에 여전히 유의미할 수 있다.
- 실제 귀무가설에 실수로 높은 가중치를 부여하더라도 $m$이 충분히 크면 FDR이 $\alpha$이하임을 위에서 보였다.
Informatrive case
이제 informative인 경우에 검정력이(또는 검정력의 비) 더 큰지 살펴보자.
임계값 $t$에 대한 함수로 제 1종 오류 $I(t)$, wBH 절차에서의 검정력 $H(t)$은 각각 아래와 같다 (BH 절차에서의 검정력은 $Pr(P\leq t|H=1)=F(t)$이다.)
\[\begin{align*} I(t) &= Pr(P\leq Wt|H=0) = \int wtdQ_0(w) = \mu_0 t \\ H(t) &= Pr(P\leq Wt|H=1) = \int F(wt)dQ_1(w) \end{align*}\]$\mu=1$로 고정되어 있기에, 유익한 경우에 제 1종 오류는 감소함을 알 수있다.
이제 $t^w,t^0$을 각각 모집단 cdf로부터 구해진 wBH절차, BH절차에서의 점근적인 임계값이라고 하자. 즉,
\[\begin{align*} &\frac{t^w}{D(t^w)} = \alpha = \frac{t^0}{G(t^0)} \end{align*}\]위 관계식을 이용하여, 최종적으로 알고 싶은 wBH절차와 BH절차에 대한 검정력의 비는 다음과 같다.
\[\frac{H(t^w)}{F(t^0)} = \frac{t^w}{t^0}[ 1 + (\mu_1-1)\frac{t^0}{F(t^0)}]\]즉 임계값 $(t^w,t^0)$의 비율에 따라 달리짐을 의미한다. 하지만 각각의 임계값도 결국 BH,wBH절차의 대립가설하의 cdf $H,F$에 의존하는 값이기에 의미 있는 해석을 할 수는 없고, 결국 알고싶은 것은 가중치를 쓰는 것이 실제로 검정력을 높이는가라는 질문에 대한 적절한 답은 아닌 것 같다.
따라서 가중치의 효과를 점진적으로 분석할 수 있도록, 다음을 고려해보자.
$Q_0$을 고정하여 $\lambda \in[0,1]$을 이용해 $W^{\lambda}=\lambda W +(1-\lambda)$라고 하자. $\lambda$는 가중치의 강도를 조절하는 모수로 해석할 수 있다.
또한, $W^{\lambda}$에 대한 wBH절차에서의 임계값을 $t^{\lambda}$; 즉 $t^{\lambda}/D^{\lambda}(t^{\lambda})=1/\alpha$라고 하자.
이제 $H(t^{\lambda})/F(t^0)$; 즉, $t^{\lambda}/t^0$의 비를 분석하여, 가중치의 강도에 따른 검정력의 비를 확인해보자.
Note. $\lambda=0$일 때, $D^{\lambda}=G, t^{\lambda} = t^0$이고, $\lambda=1$일 때의 $D^{\lambda} = H, t^{\lambda} =t^w$이다.
1차 테일러 근사를 통해, $t^{\lambda} \approx t^0 + \frac{dt^{\lambda}}{d\lambda}|_{\lambda=0} \cdot \lambda$임을 알 수 있다. 따라서, $dt^{\lambda}/d\lambda$을 구해보자.
먼저, 다음의 관계식이 성립한다.
\[\begin{align*} &\frac{D^{\lambda}(t^{\lambda})}{t^{\lambda}} - \frac{G(t^0)}{t^0} = 0 \\ &\frac{(1-a)(\lambda\mu_0+(1-\lambda))t^{\lambda} + a\int F((\lambda w+1-\lambda)t^{\lambda})dQ_1(w)}{t^{\lambda}} - \frac{(1-a)t_0+aF(t_0)}{t^0} =0 \\ &\lambda(1-a)(\mu_0-1) + a\frac{\int F((\lambda w+1-\lambda)t^{\lambda})dQ_1(w)}{t^{\lambda}} - a\frac{F(t_0)}{t_0} = 0 \\ &-\lambda a(\mu_1 - 1) + a\frac{\int F((\lambda w+1-\lambda)t^{\lambda})dQ_1(w)}{t^{\lambda}} - a\frac{F(t_0)}{t_0} = 0 \end{align*}\]따라서,
\[R(t,\lambda) = \frac{\int F((\lambda w+1-\lambda)t)dQ_1(w)}{t}-(\mu_1 - 1) - \frac{F(t_0)}{t_0}\]에 대해 $R(t^{\lambda},\lambda)$는 $\lambda \in [0,1]$에서 항상 $0$이다. 따라서, 음함수 정리에 의해 다음이 성립한다.
\[\frac{dt^\lambda}{d\lambda}\bigg|*{t^0, 0} = - \frac{\partial R / \partial \lambda}{\partial R / \partial t}\bigg|*{(t, \lambda)=(t^0, 0)} = (\mu_{1}-1)t^{0}\frac{f(t^{0})-t^{0}}{F(t^{0})-t^{0}f(t^{0})}\]이를 위 1차 테일러 근사식에 대입하면 아래와 같다.
\[\frac{t^{\lambda}}{t^0} \approx 1 + \lambda(\mu_{1}-1)t^{0}\frac{f(t^{0})-t^{0}}{F(t^{0})-t^{0}f(t^{0})}\]그러므로, 검정력의 비는 다음과 같다.
\[\frac{H(t^{\lambda})}{F(t^0)} = [1 + \lambda(\mu_{1}-1)t^{0}\frac{f(t^{0})-t^{0}}{F(t^{0})-t^{0}f(t^{0})}][ 1 + (\mu_1-1)\frac{t^0}{F(t^0)}]\]또한, $F$는 순오목함수임으로, 접선이 항상 $F$보다 위에 있다. $F(0)=0$에 대해 비교하면,
\[0 < F(t) + f(t)(0-t) = F(t) - tf(t) \ (t\neq 0)\]즉, 유익한 경우(Informative case, $\mu > 1$)인 경우에 대해 $f(t^0) > t^0$이면 검정력은 항상 BH절차보다 좋음을 알 수 있다.
$F$는 순오목 함수인 경우에 대해서만 다루고 있고, cdf는 단조증가함수이기에, 이에 대한 도함수 $f$는 단조 감소함수이다. 또한, $t^0 = \alpha G(t^0)\geq \alpha$이다. 따라서, $f(\alpha) > \alpha$인 경우에 대하여, 다음과 같이 $f(t^0) >t^0$이 성립한다.
\[f(t^0) \geq f(\alpha) > \alpha \geq t^0\]이제, 대립가설하의 검정통계량 분포가 $\mathcal{N}(\theta,1)$인 경우에 대해 $f_{\theta}(\alpha)>\alpha$; 즉 power arbitrage가 발생하는 $\theta$의 범위를 직접 구해보자. (귀무가설의 분포는 $\mathcal{N}(0,1)$)
만약 단측검정을 한다고 가정하면 p-value $t$와 관측된 검정통계량 $x$간의 관계는 $t = 1-\Phi(x)$; $x = \Phi^{-1}(1-t)$이다. 따라서,
\[\begin{align*} f_\theta(t) = f(x)|\frac{dx}{dt}| = \phi(x-\theta) \cdot \frac{1}{\phi(x)} = \exp(-\frac{\theta^2}{2} +\theta \Phi^{-1}(1-t))\\ \end{align*}\]이를 $f_{\theta}(\alpha) > \alpha$인 관계식에 대입하면 다음과 같은 $\theta$의 범위가 나온다.
\[0 \leq \theta \leq \Phi^{-1}(1-\alpha) + \sqrt{(\Phi^{-1}(1-\alpha))^2-2\log \alpha}\]즉, 대립가설의 분포의 모수가 위 구간에 있을경우 wBH절차의 검정력이 더 좋음을 보장할 수 있다. 직관적으로, $\theta$가 $0$에서 벗어날수록 귀무가설과의 분포와 많이 달라지기에 가설검정이 더 쉬운 경우라고 볼 수 있다. 이러한 경우에 대해서는 반드시, BH절차에 비해 검정력이 좋음은 보장할 수 없다.
다음은 wBH절차와 BH절차의 검정력의 비를 나타낸 그래프이다. $\alpha=0.05$, 대립가설의 비 $a=0.05$로 고정한채로 대립가설의 분포가 $\mathcal{N}(\theta,1)$일 때, 효과의 크기에 대한 모수 $\theta$를 x축으로, 사전 정보를 활용한 가중치의 유익함 $\mu_1$을 y축으로 하여 검정력의 비 $H(t^w)/F(t^0)$를 등고선으로 나타내었다.
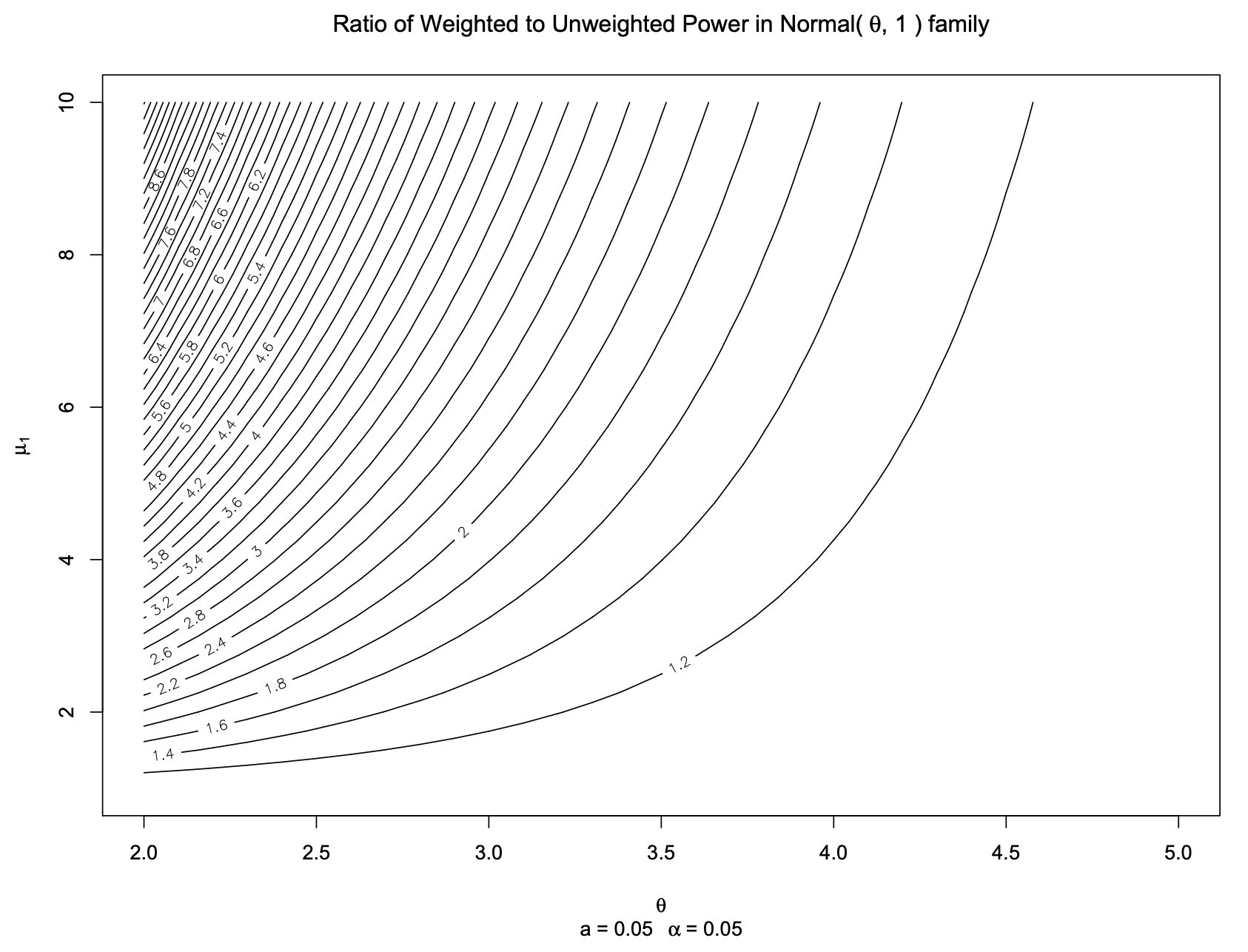
효과의 크기가 적을수록, 즉 귀무가설과 대립가설의 차가 미미해서 발견하기 어렵고, 가중치의 유익함이 큰 경우 검정력의 비가 가장 차이가 크게 나고 있음을 알 수 있다.
또한, 위 식에서 $\alpha=0.05$에 대한 유익한 가중치일 구간이 $\theta \in [0, 4.59]$지만, 실제 검정비가 $1$이 되는 지점은 이보다 훨씬 오른쪽에 위치해 있음을 알 수 있다.
지금까지 사전 정보를 가중치로 활용하여 검정력을 높이는 wBH 절차를 살펴보았고, 이 절차가 어떤 표본 크기에서든 FDR을 안전하게 통제함을 보였다. 또한 가중치를 사용하지 않는 경우보다 검정력의 비가 더 높음을 통해 더 나은 절차임을 보였다.
다음은 가중치를 어떻게 찾아야하는지에 대한 한가지 방법론을 소개한다.
검정력을 최대로 하는 가중치
Roquain & van de Wiel (2009). wBH 절차가 FDR을 $\alpha$이하로 통제할 수 있음을 보였지만, 검정력의 경우 특정한 조건에서 WH 절차에 비해 검정비가 좋아짐을 보였다. 이번에는 검정력을 최대화하는 절차를 알아볼 것이다.
이는 네이만-피어슨 보조정리의 기각역의 형태에서 아이디어를 빌려 제안되었다. 기존 wBH 절차의 임계값은 아래와 같다.
\[\hat{t} = \max\{Q_{(i)}: Q_{(i)} \leq \alpha \cdot\frac{i}{m}\}\]이제 $\hat{t}$보다 작거나 같은 $P_i/W_i$를 기각한다. 만약 $\hat{t} = Q_{(r)}$이라면 $r$개의 가설이 기각된다. 따라서 기각되는 가설의 비율은 $r/m$이다. 이러한 비율은 절차와 임계점의 정의상 임계점과 일대일 대응임을 알 수 있다. 따라서, 임계점을 기각되는 가설의 비율로 다음과 같이 나타낼 수 있다. ( 가중치는 $W$$\sum_iW_i=m$를 만족하는 사전에 정해진 고정된 상수벡터로 가정한다.)
\[\begin{align*} \hat{u} &= m^{-1} \cdot\max\{r\in \{1,...,m\}:Q_{(r)}\leq \alpha \cdot \frac{r}{m}\} \\ &= \sup\{u:\hat{G}_W(u) \geq u\} \text{ where } \hat{G}*W(u) = m^{-1}\sum*{i=1}^m I[P_i \leq \alpha W_iu] \end{align*}\]즉 개별 가설마다 $P_i \leq \alpha W_i u$이면 기각한다는 기준을 정해서, 전체 가설 $m$개 대해 모두 시행하였을 때 만족해야하는 기각비율 $u$보다 큰; 즉, 실제로 유효한 기각비율 $u$의 상한을 찾겠다는 의미이다.
따라서 최적의 가중치를 찾는 과정에서는 개별 가설마다의 $P_i \leq \alpha W_i u$의 기각역을 고려해야하고, 검정력을 최대화 하기 위해 다음과 같이 수준 $\alpha W_iu$하에서의 검정력이 기각 비율 $u$인 wBH절차의 검정력에 대응된다.
\[Pow_u(W) = Pow(\{i:P_i \leq \alpha W_i u\})\]Note. 기각되는 비율 $u$는 0과 1사이의 연속적인 값을 갖겠지만, 실제 관측에서는 $0,1/m,…,1$의 이산적인 값을 갖는다.
이를 기각비율 $u$가 주어지고, 이에 대해 검정력을 최대로하는 가중치 $W(u)$를 찾는것이 목표이다.
- 모든 $i=1,…,m$ $i$$W_i(u)u$는 단조 증가한다.
- 모든 $u \in(0,1]$에 대해 $\sum_iW_i(u)=m$이다.
자연스럽게 최적의 가중치(optimal weight function)는 모든 $u$에 대해 $Pow_u$가 최대인 함수이다.
네이만-피어슨 보조정리에 의하면, 유의 수준 $\alpha$하에서 두 가설을 비교할 때, 우도비(likelihood ratio)가 특정 임계값보다 큰 경우를 기각하는 것이 최강력 검정임을 보장한다. 이를 비유하여, $u$가 주어진 상태에서 각 가설 $i$의 최적 기각역을 우도비꼴로 나타낸다. 귀무가설하의 p-value의 pdf는 $1$이고, $F_i$의 pdf를 $f_i$라 하면 다음과 같은 꼴이다.
\[\frac{f_i(P_i)}{1} \geq y^*(u)\] \[W_i^*(u) = (\alpha u)^{-1}f^{-1}_i(y^*(u))\]\(y^*(u)\)는 \(\sum_i W^*_i=m\)의 제약조건을 만족시키는 값이다. 즉, $\sum_i(\alpha u)^{-1}f^{-1}_i(y^*(u))=m$
결과적으로 절차는 다음과 같다.
- $r=m,..,1$의 순서로 내려오면서 탐색
- 각 단계에서 $W^*(r/m)$을 부여한 가중치 $Q_{(r)} \leq \alpha \cdot (r/m)$을 만족하는지 확인한다.
- 이 조건을 만족하는 첫 번째 $r$을 찾으면, 그 즉시 절차를 멈추고, 현재 단계의 $Q_{(1)},…,Q_{(r)}$에 대응하는 가설들을 기각한다.
지금까지 side information를 통한 군집화, 가중치 기반의 다중검정방법론들을 다뤄보았다. 다음 포스팅에서는 p-value기반의 방법론들을 알아보려한다.
