다중 검정에서 사전정보를 활용하여 p-value마다 가중치를 부여하여 검정하는 방법을 알아볼 예정이다.
Genovese, C. R., Roeder, K., & Wasserman, L. (2006) False Discovery Control With P-Value Weighting의 내용을 참고하였다.
BH 절차 (Benjamini-Hochberg Procedure)
전통적인 Bonferroni 교정 등은 전체 오류 발생 확률(FWER)을 매우 엄격하게 통제하기 때문에, 진짜 효과가 있더라도 이를 발견하지 못할(낮은 검정력) 가능성이 크다.
BH 절차는 이보다 완화된 기준인 FDR(False Discovery Rate, 거짓 발견율)을 통제한다.
FDR은 기각된 가설들 중 실제로 참인 귀무가설(잘못 기각된 가설)의 비율에 대한 기댓값으로, BH 절차는 이 비율을 특정 수준(e.g. 0.05)이하로 유지하면서도 검정력을 높일 수 있는 방법이다.
- $m$개의 가설에 대한 각각의 p-value를 오름차순으로 정렬한다: $0=P_{(0)}\leq P_{(1)}\leq…\leq P_{(m)}$
- $mP_{(i)} \le \alpha i$를 만족하는 가장 큰 $P_{(i)}$를 구해서 이를 임계값 $T$로 설정한다.
- $T$보다 작거나 같은 모든 p-value에 대응하는 가설을 기각한다.
실제 귀무가설의 수를 $m_0$라고 할 때, BH 절차는 FDR을 $\alpha m_0/m$로 통제할 수 있다.
BH 절차의 한계
BH 절차의 핵심적인 한계는 모든 귀무가설을 서로 교환 가능한(interchangeably)것으로 취급한다. 즉, 모든 가설이 동등하게 다뤄지며, 각 가설이 가진 고유한 맥락이나 사전 정보가 전혀 고려되지 않는다.
하지만, 실제 과학 연구에서는 모든 귀무가설이 동등하게 만들어지지 않는다. 예를 들어, fMRI 연구에서는 특정 뇌 영역이 특정 자극에 반응할 것이라는 해부학적 정보가 있을 수 있고, 유전학 연구에서는 선행 연관 분석을 통해 특정 유전체 영역이 질병과 관련 있을 가능성이 더 높다는 사전 정보를 가질 수 있다.
이러한 한계를 극복하기 위해 가설에 가중치(weights)를 부여하는 접근법들이 제안되었다.
가설에 가중치를 부여하는 방식
가설에 가중치를 부여하는 방식은 p-value에 부여하는 방법과 손실이나 오류의 기준(FDR)에 부여하는 2가지 방법이 있다.
p-value 가중치에서 높은 가중치를 부여하는 기준은 귀무가설이 거짓일 것이라는 사전 확률이다. 즉, 연구자는 진짜 효과가 있을 것 같다고 예측하는 가설에 높은 가중치를 준다.
e.g. 선행 연구에서 특정 유전자가 질병과 관련이 있을 것이라는 강력한 증거가 나왔다면, 이번 연구에서 해당 유전자에 대한 가설에 높은 p-value 가중치를 부여하여 검출될 가능성을 높인다.
손실 가중치에서 높은 가중치를 부여하는 기준은 해당 가설에서 잘못된 발견(False Discovery)을 했을 때 발생하는 위험이다. 즉, 잘못 기각하면 더 위험이 크다고 판단되는 가설에 높은 가중치를 둔다.
p-value 통계량의 확률 분포
여기서는 p-value 기반 가중치 부여 방식에 중점을 둔다. p-value 통계량 $P^m = (P_1,…,P_m)^T$을 귀무가설과 대립가설인 경우에 대한 mixture model로 나타낼 수 있다.
귀무가설일 경우 $H_i=0$이고, 대립가설일 경우 $1$로 나타내면, 대립가설의 비율을 $a (0<a<1)$로 하여 가설에 대한 통계량을 $H_i \sim Ber(a)$를 통해 $H^m=(H_1,…,H_m)^T$로 나타낼 수 있다.
Note. 독립성과 교환 가능성
-
독립성 (Independence): 데이터의 통계적 속성에 대한 가정이다. e.g. $H_i$들은 서로 독립이다.
-
교환 가능성 (Interchangeability): 분석 절차의 속성에 대한 가정이다. 분석가가 모든 가설을 구별할 사전 정보가 없어서, 모든 가설을 동일하게 취급한다는 의미이다. BH 절차가 이 교환 가능성을 바탕으로 한다.
먼저, 귀무가설이 참인 경우에 대해 p-value의 확률분포를 가정해보자.
귀무가설이 참일 때에 검정통계량 $X \sim F_X$를 따른다고 하고, 관측된 검정 통계량을 $x_{obs}$라고 하자. 이 때, 단측 검정을 예로 들면 p-value는 다음과 같다.
\[Pr(X\leq x | H_0) (\text{또는 } Pr(X\geq x | H_0))\]따라서 귀무가설이 참이면, 각각은 $F_X(x_{obs})$ (또는 $1-F_X(x_{obs})$)이고, 확률적분변환에 의해 이는 $Unif[0,1]$을 따른다.
이제 대립가설인 경우에 대해 p-value의 확률본포를 가정해보자.
대립가설인 경우에는 p-value에 대한 확률분포는 대립가설인 경우에 $\zeta$를 p-value의 cdf에 대한 확률변수로 정의하고 이에 대한 cdf를 $\mathcal{L}(\zeta)$라고 하자. 즉, $i$번째 대립가설이 참인 경우, p-value는 $\zeta_i$를 따른다.
이러한 cdf들의 기댓값 $F = \int \zeta d\mathcal{L}(\zeta)$ ( 추가적으로 $F$는 균등분포보다 더 극단적인 값에서 더 높은 확률을 갖도록 가정한다.)라고 하면, $P_i$의 주변확률분포는 다음을 따른다.
\[\begin{align*} &P_i|_{H_i=0, \zeta_i} \sim Unif[0,1] \\ &P_i|_{H_i=1, \zeta_i} \sim \zeta_i \\ &P_i \sim (1-a)U + aF \end{align*}\]이제 $P_i$의 주변부 cdf를 $G=(1-a)U + aF$라고 하자.
p-value 가중치의 확률분포
다음은 결합 확률분포 $(H,W,P)$의 가정이다. 관측할 수 없는 실제 가설의 상태 $H$가 p-value $P$를 결정하며, 또한 BH의 한계를 극복하기 위해 가중치를 도입하기 위해 실제 가설의 상태 $H$가 가중치 $W$에 영향을 준다.
또한 p-value는 관측으로부터 주어지며, 가중치는 이러한 관측과는 독립적으로 사전에 주어져야 하므로, $H$가 주어졌을 때에 $P,W$는 독립이어야 한다.
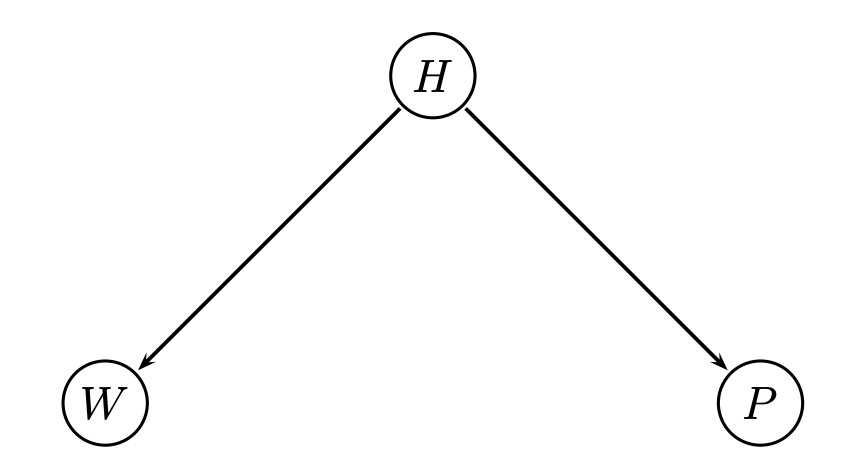
가중치 $W^m=(W_1,…,W_m)^T$의 분포에 대해서는 $P^m$에서와 비슷하게 귀무가설/대립가설인 경우의 조건부 cdf를 support $(0,\infty)$인 $Q_0,Q_1$을 각각 가정한다.
\[W_i \sim (1-a)Q_0 + aQ_1\]따라서, 가중치가 부여된 p-value $P/W$의 cdf $D$는 다음과 같다. 이는 $H$가 주어졌을 때에 $P$와 $W$는 독립이라는 가정과 적절한 조건(e.g. 합과 적분의 순서를 바꿀 수 있음)하에서 전체 확률의 법칙과 베이즈 정리를 통해 유도될 수 있다.
\[\begin{align*} D(t) &= Pr(\frac{P}{W}\leq t)=\int\sum_{h=0}^1Pr(P\leq wt|H=h)f(h|w)dQ(w)\\=& \sum_{h=0}^1\int Pr(P\leq wt)dQ(w|h)f(h) = (1-a)\mu_0t + a\int F(wt)dQ_1(w) \end{align*}\]Note. \(\mu_0 = \mathbb{E}[W|H=0] = \int wdQ(w|H=0) = \int wdQ_0(w)\) :귀무가설 하에서 가중치의 기댓값
Note. \(Pr(P/W \leq t|H=0) = tw, Pr(P/w \leq t|H=1) = F(tw)\)
Note. \(f(h|w)dQ(w) = dQ(w|h)f(h)\) ($f(h)$는 $Ber(a)$의 pmf)
즉, 귀무가설과 대립가설의 기여분으로 나누어 표현할 수 있다.
wBH 절차
먼저 FDR(False Discovery Rate)을 정의하자. 만약, 임계값 통계량 $T$를 이용하여, 이보다 작은 p-value를 갖는 가설들을 기각한다고 하면 FDP(false discovery proportion, 잘못 기각된 비율)는 다음과 같이 정의한다.
\[FDP(T) = \frac{\sum_iI(P_i \leq t)(1-H_i)}{\sum_i I(P_i\leq t)}\]이에 대한 기댓값을 FDR이라고 정의한다.
\[FDR = \mathbb{E}_T[FDP(T)]\]이제 FDR을 통제하면서 사전정보 기반 가중치가 더해진 p-value 통계량 $Q^m=(Q_1,…,Q_m)^T$( $Q_i=P_i/W_i, W_i >0$)을 사용하는 wBH 절차를 정의할 수 있다.
먼저, BH 절차에서의 임계값을 살펴보자.
\[T_{BH} = \max \{P_{(i)}: P_{(i)} \leq \alpha\cdot\frac{i}{m} \}\]여기서 p-value의 주변부 cdf $G$에 대해 $m$개의 샘플로 구한 empirical cdf는 다음과 같다.
\[\hat{G}_m(t) = \frac{\sum_iI(P_i \le t)}{m}\]즉, \(\hat{G}_m(P_{(i)}) = i/m\)임을 알 수 있다. 따라서 임계값을 아래와 같이 다시 쓸 수 있다.
\[T_{BH} = \max \{t \in \{P_{(1)},...,P_{(m)}\}: t \leq \alpha \hat{G}_m(t) \}\]또한, 임계값을$ P_{(i)}$라 하면 임의의 $j>i$인 $P_{(j)}$에 대해서는 \(P_{(j)} > \alpha \hat{G}_m(t)\)이며, \(P_{(i)} \leq t < P_{(i+1)}\) 인 $t$들에 대해서는 $\hat{G}_m(t) = i/m$이다. 하지만, 이 구간에서 어떤 임계점을 잡아도 결국 기각되는 가설의 수는 변함이 없으므로 BH절차의 임계값은 다시 다음처럼 쓸 수 있다.
\[T_{BH} = \sup\{t:\hat{B}(t)\leq \alpha \} \text{ where } \hat{B}(t) = \frac{t}{\hat{G}_m(t)}\]자연스럽게 wBH 절차는 $\hat{B}(t)$에서 p-value의 empirical cdf를 가중치가 반영된 p-value $Q$에 대한 empirical cdf $\hat{D}(t)$를 가중치의 표본 평균 $\bar{W}_n$으로 나눈 값으로 대체하여 임계값을 계산한다.
\[T_{wBH} = \sup\{t:\hat{R}(t)\leq \alpha \} \text{ where } \hat{R}(t) = \frac{t\bar{W}_m}{\hat{D}(t)} = \frac{t\sum_iW_i}{\sum_{i}I(P_i\leq W_it)}\]이를 $Q_{(i)}$로 나타내면 아래와 같다.
\[T_{wBH} = \sup\{t: t \leq \alpha \frac{\sum_{i}I(Q_i\leq t)}{\sum_jW_j}\} = \sup\{Q_{(i)}: Q_{(i)} \leq \frac{\alpha i}{\sum_jW_j}\}\]마찬가지로 임계값은 $Q_{(i)}$를 기준으로 기각되는 수가 달라지고, $\sum_jI(Q_j\leq Q_{(i)}) = i$이기 때문이다. 이제$\alpha k /\sum_jW_j$를 $q_k$라고 하자.
FDR의 상한 (가설의 수가 유한한 경우)
이제, wBH 절차가 FDR을 $\alpha$이하로 통제할 수 있는지 확인해보자. 먼저 유한개의 가설에 대한 경우부터 고려해보자.
$H^m$이 주어졌을 때 조건부 FDR을 먼저 계산하고, 조건부기댓값의 성질을 통해 $FDR$이 어떤 값을 갖는지 살펴보자.
\[\mathbb{E}[FDP(T_{wBH})|H^m] = \mathbb{E}[\frac{\sum_{i:H_i=0}I(Q_i \leq T_{wBH})}{\sum_jI(Q_j\leq T_{wBH})}|H^m]\]위는 여러개의 확률변수가 있어서 전체 확률의 법칙으로 쉽게 풀기 위해 다음과 같은 경우를 생각해보자.
$f_i(k) = \sum_{j \neq i}I(Q_i \leq q_k)+1, k=1,…,m$이라면 $f_i(k)$또한 $1,…,m$의 값을 갖는 단조증가함수이므로, $k=f_i(k)$인 $k$가 반드시 존재한다. 따라서, 아래와 같은 사건 $R_{k,i}$를 정의하면 $R_{1,i},…,R_{m,i}$들은 서로 배반사건이며 위의 $f_i$에 $Q^m$을 대입하면, $Q^m$은 반드시 $R_{1,i},…,R_{m,i}$중 하나에 속한다.
\[R_{k,j} = \{Q^m:\sum_{j\neq i}I(Q_j \leq q_k) = k-1\}\]즉, $R_{1,i},…,R_{m,i}$를 사용하여 전체확률의 법칙을 사용한다.
\[\mathbb{E}[FDP(T_{wBH})|H^m] = \sum_{i : H_i=0}\sum_{k=1}^m \mathbb{E}[\frac{I(Q_i \leq T_{wBH})}{\sum_jI(Q_j\leq T_{wBH})}|H^m,R_{k,i}]Pr(R_{k,i}|H^m)\]이제 조건부 기댓값 내부를 보자. $Q^m \in R_{k,i}$인 경우이므로 $Q_i > k$이면, $T_{wBH}$의 정의에 의해 분자의 지시함수가 $0$이 되고, 반대인 경우는 분자는 $1$, 분모가 $k$가 된다. 즉, 다음이 성립한다.
\[\mathbb{E}[\frac{I(Q_i \leq T_{wBH})}{\sum_jI(Q_j\leq T_{wBH})}|H^m,R_{k,i}] = \frac{1}{k}Pr(Q_i\leq q_k)\]따라서, $Q_i=P_i/W_i$로 쪼개어 $P$에 대한 주변부 분포를 구하면 아래와 같다.
\[\begin{align*} \mathbb{E}[FDP(T_{wBH})|H^m] &= \sum_{i : H_i=0}\sum_{k=1}^m \frac{1}{k}Pr((Q_i\leq q_k) \cap R_{k,i}|H^m) \\ &= \sum_{i : H_i=0}\sum_{k=1}^m \frac{1}{k} \mathbb{E}[Pr((P_i\leq W_iq_k) \cap R_{k,i}|H^m,W^m)|H^m ] \end{align*}\]이제 $P^m$에 대한 조건부 분포로 주어지고, 각각의 $R_{k,i}$의 정의에 의해들은 위의 두 사건은 독립으로 교집합을 각각의 확률의 곱으로 쪼갤 수 있으며, $H_i=0$로 주어진 상태에서 $P_i$들은 균등분포를 따르기에 다음과 같이 쓸 수 있다.
\[\begin{align*} \mathbb{E}[FDP(T_{wBH})|H^m] &= \sum_{i : H_i=0} \mathbb{E}[\frac{\alpha W_i}{\sum_j W_j}\sum_{k=1}^m Pr(R_{k,i}|H^m,W^m)|H^m ] \\ &= \sum_{i : H_i=0} \mathbb{E}[\frac{\alpha W_i}{\sum_j W_j}|H^m ] \end{align*}\]따라서 $\sum_j W_j=m$이 되도록 가중치를 잡으면 FDR은 아래와 같다.
\[\begin{align*} FDR &= \mathbb{E}[FDP] = \mathbb{E}[\mathbb{E}(FDP|H^m)] \\ &= \mathbb{E}[\frac{\alpha \mu_0}{m}\sum_i (1-H_i)] = \alpha \mu_0 (1-a) \end{align*}\]또한 가중치의 기댓값 $\mu = (1-a)\mu_0 + a\mu_1$이며 마찬가지로 $\sum_j W_j=m$ (즉,$\mu=1$)로 잡는다면, $\mu_0 \leq (1-a)^{-1}$이다. 이 부등식을 위 FDR에 대입하면 항상 $\alpha$보다 작거나 같음을 알 수 있다.
Note. 이는 앞에서 정의한 $Q$의 cdf $D(\alpha)$에서의 귀무가설의 기여분과 같다.
즉 wBH절차는 다음과 같이 수행될 수 있다.
- 사전 정보를 이용하여 $\sum_iW_i=m$, $W_i>0$가 되도록 $W^m=(W_1,…,W_m)^T$을 구한다.
- 실제 실험을 통해 $m$개의 가설에 대한 p-value를 구해 $Q_i=P_i/W_i$를 계산한다.
- 이제 $Q^m=(Q_1,…,Q_m)^T$에 대해 BH 절차를 수행한다.
이번 포스팅에서는 wBH절차가 FDR을 $\alpha$이하로 통제할 수 있음을 보였다. 하지만, 이는 귀무가설에 대한 가중치의 기댓값과, 모비율 $\mu_0, (1-a)$에 의존하는 수동적인 상한이다. 다음 포스팅에서는 충분히 큰 $m$인 경우의 데이터에만 의존하는 FDR의 상한을 유도하여 마찬가지로 $\alpha$이하로 통제함을 보일 예정이다. 즉 BH와 같이 $\alpha$이하로 통제함으로 마지막으로, wBH절차가 BH절차보다 더 검정력이 좋음을 밝혀 더 나은 절차임을 설명할 것이다.
