Grouping based multiple testing

다중 검정에서 가설들이 교환가능하지 않을 경우, 군집화를 기반으로 이를 해결하는 방법론들을 다뤄볼 것이다. 다음의 내용을 참고하였다.

Efron, B. (2008) Simultaneous inference: When should hypothesis testing problems be combined?

Cai, T. T. and W. Sun (2009) Simultaneous Testing of Grouped Hypotheses: Finding Needles in Multiple Haystacks

Barber and Ramdas (2017) The p-filter: multi-layer FDR control for grouped hypotheses

Random mixture model in multiple testing

\[\begin{align*} &X \sim F(x) = (1-p)F_0(x) + pF_1(x) \\ &f(x) = (1-p)f_0(x) + pf_1(x) \end{align*}\]

• \(p\)는 prior로 null이 아닌 샘플의 비율로 일반적으로 0.1 이하로 잡는다.
• \(f_0\)은 null에서의 pdf로 일반적으로 정규분포를 사용한다 ( \(F_0\)의 경우는 cdf)

Efron(2008). Bayesian

False discovery rate

\[Fdr(x) = Pr(\text{x is null}| \text{x is in critical region} )\]

Note. 베이즈 정리에 의해 유의 수준 \(\alpha\)에 대해 다음의 관계를 갖는다.

\[Fdr(x) = \alpha \cdot (1-p)/Pr(\text{x is in critical region})\]

• p-value 기반 본페로니 교정(Family-Wise Error Rate, FWER): $m$개의 검정 중, 단 한 개의 거짓 발견이라도 발생할 확률을 제어
• FDR 기반 검정: 최종적으로 발견이라고 선언한 목록 중에서, 거짓 발견의 비율을 제어

local false discovery rate

\[fdr(x) = Pr(\text{x is null}| \text{x is critical value} )\]

이게 더 일반적인 정의이다.

Benjamini and Hochberg’s (1995)

control level \(q\)(일반적으로 \(q = 0.1\))을 설정하여, 아래의 Fdr 추정량이 \(q\)가 되는 \(z_{max}\)를 구하고, 이를 통한 기각역에 따라 이를 넘어가는 통계량에 대응하는 가설을 기각한다.

\[\bar{Fdr}(x) = (1-p)F_0(x) / \bar{F}(x)\]

• \(\bar{F}(z)\)는 경험적 cdf

Sun and Cai (2007). Frequentist

False discovery rate

\[FDR = \mathbb{E}(N_{10}/R)Pr(R>0)\]

The marginal FDR (mFDR)

\[mFDR = \mathbb{E}(N_{10}) / \mathbb{E}(R) = FDR + \mathcal{o}(m^{-1/2})\]

즉, multiple testing인 상황에서는(\(m \rightarrow \infty\)) FDR로 근사될 수 있다.

False non-discovery rate

\[FNR = \mathbb{E}(N_{01}/S|S>0)Pr(S>0)\]

FDR이 제 1종 오류에 대응된다면, FNR은 제 2종 오류에 대응한다.

FDR 절차는 사전에 지정된 수준 \(\alpha\)에서 FDR을 제어할 때 유효하며, 수준 \(\alpha\)에서 모든 FDR 절차 중 가장 작은 FNR을 가질 때 최적이라고 한다.

\(\delta_i =1\)일 때, \(H_i\)를 기각하고, 아니면 0이라고 하여, \(m\)개의 가설에 대해 \(\delta = (\delta_1,...,\delta_m)^T\)을 통해 general decision rule을 정의하자.

만약 \(F\)가 알려진 경우, 수준 \(\alpha\)에서 최적의 FDR 절차는 다음과 같다. (Sun and Cai (2007)) \(\delta(Lfdr, c_{OR}(\alpha) \mathbf{1}*m) = (I[Lfdr(x_1) < c*{OR}(\alpha) ], ..., I[Lfdr(x_m) < c_{OR}(\alpha) ])^T\)

• \(c_{OR}(\alpha) = \sup \{ c\in(0,1): FDR(c) \leq \alpha\}\)는 수준 \(\alpha\)에서 \(c\)를 통한 FDR 절차에서의 \(Lfdr\) 통계량의 optimal cutoff
• \[Lfdr(x) = (1-p)f_0(x)/f(x)\]

실제 구현에서는 모든 \(c \in (0,1)\)에 대해서 \(FDR\)을 계산해 최적의 cut-off를 계산하는데에는 비용이 많이 들기에, 다음과 같이 oracle procedure를 근사한다.

\[\text{Reject all } H_{(i)}, \ i=1,...,l, \text{ where } l = \max \{ i : \frac{Lfdr_{(1)}+...Lfdr_{(i)}}{i} \leq \alpha \}\]

• \(Lfdr_{(j)}\)는 \(Lfdr_{(1)} \leq ... \leq Lfdr_{(m)}\)
• 실제 추정시에는 \(\hat{Lfdr} = (1-\hat{p})\hat{f}_0/ \hat{f}\)

The multiple-group model

heterogeneous인 경우에 대해서는 각각의 그룹 내에서는 $i.i.d$ 하도록 아래와 같이 $K$개의 그룹으로 나누어 각각의 \(F_{k0}\)하에서 검정을 수행한다.

다음은 각각 normal/dyslexic인 학생 6명씩 총 12명의 학생에 대해 뇌의 15443개의 복셀에 대해 특정 z축에서의 각 복셀마다의 측정값이 두 집단에 대해서 다른지를 검정하는 통계량을 나타낸 것이다. x축의 특정 지점을 기준으로 뇌의 앞/뒤에서 검정통계량의 분포가 다름을 알 수 있다. 즉, heterogeneous한 통계량이다.

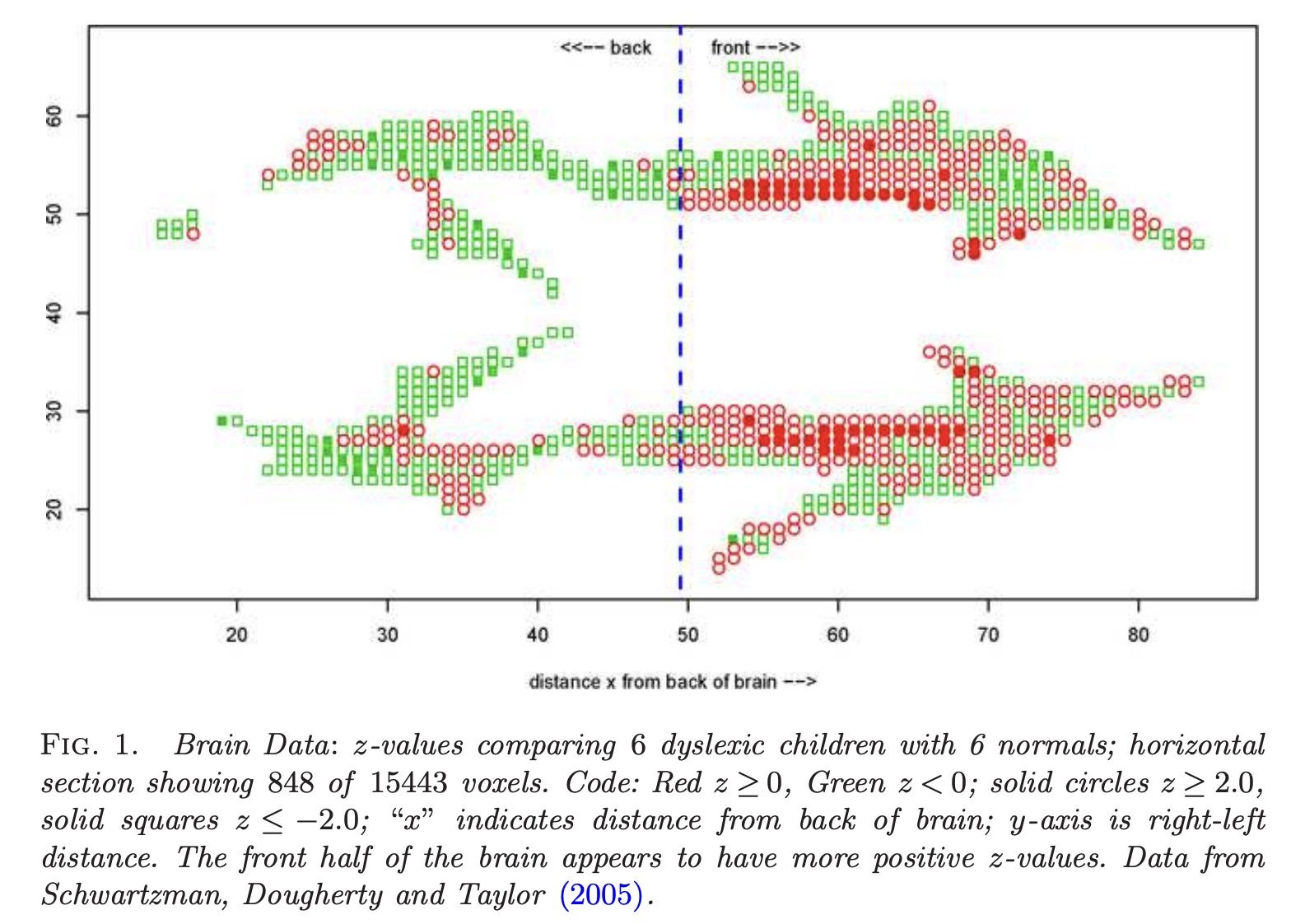
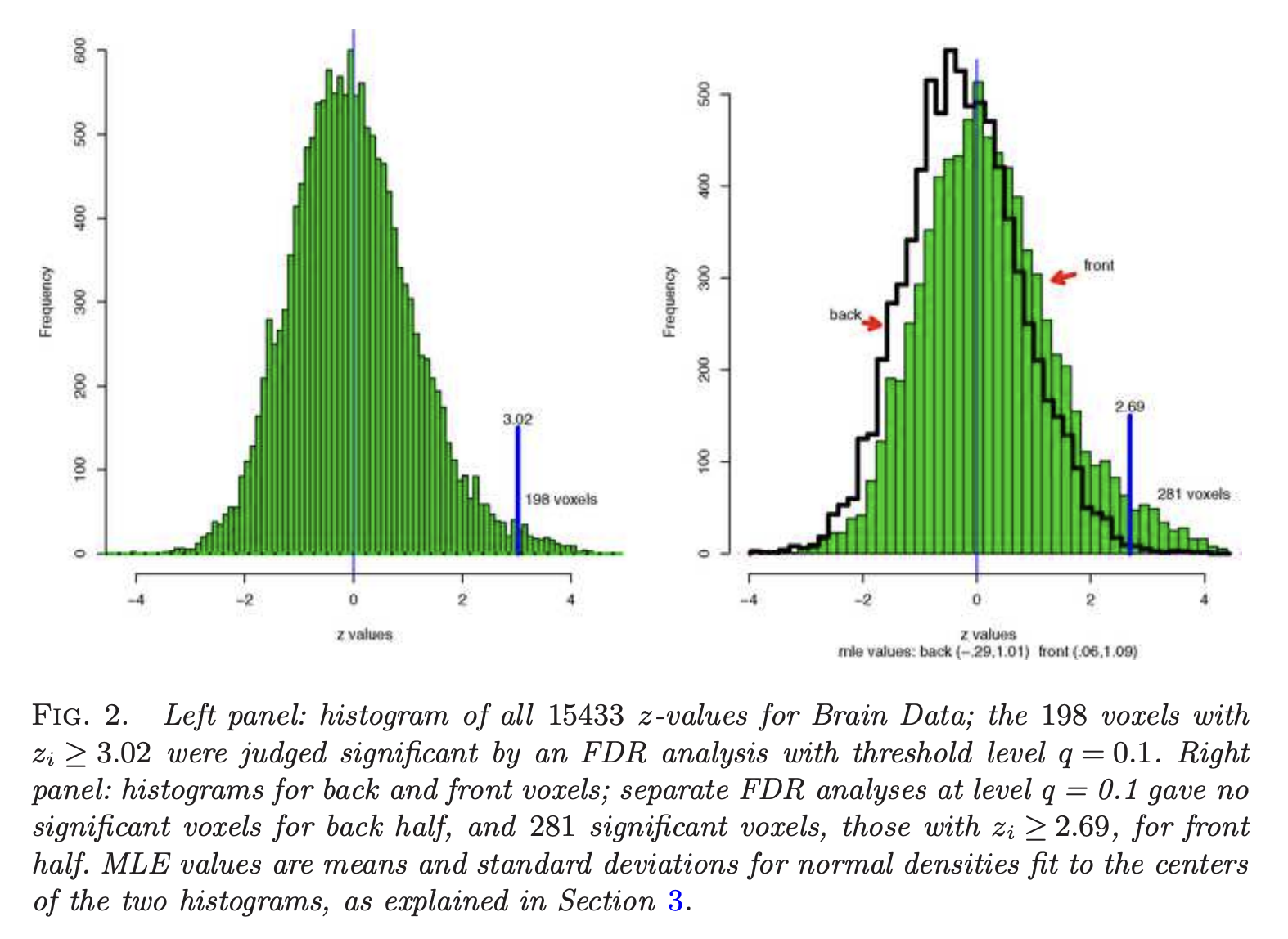
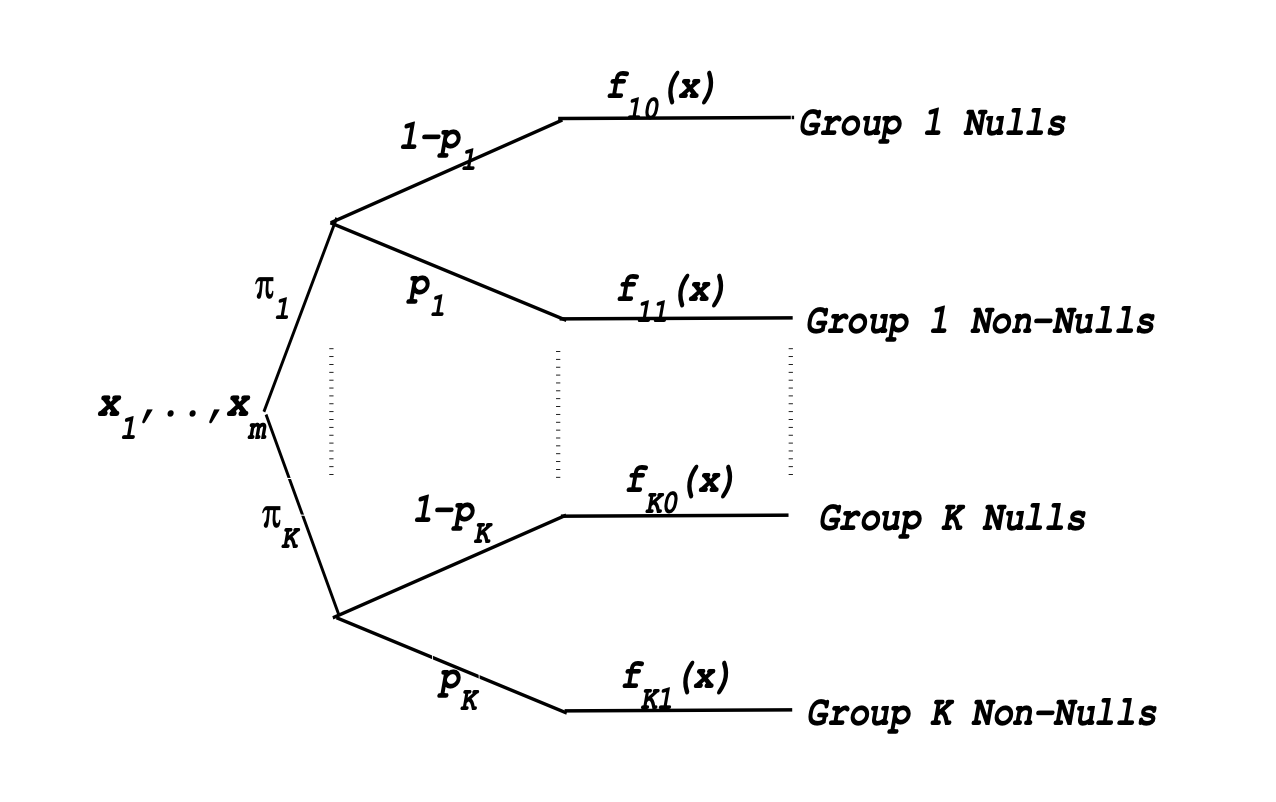\(X_{ki}|\theta_{ki} \sim (1-\theta_{ki})F_{k0} + \theta_{k1}F_{k1}, \ i=1,...,m_k, k=1,...,K\)

• \(m_k\)는 그룹 \(k\) 내에서의 가설의 수이다.
• \(\theta_{ki} \sim Ber(p_k)\), \(i=1,...,m_k\): 0이면 null이고 1이면 non-null을 나타낸다.
• 즉, \(X_{ki}\)는 i.i.d로 \((1-p_k)F_{k0} + p_kF_{k1}\)를 따른다.

이러한 random mixture model 하에서

\[N_{10} = \sum_{i=1}^m I(\theta_i=0, \delta_i = 1)\]

즉 $x$가 주어졌을 때 $N_{10}$의 조건부 기댓값은 다음과 같다.

\[\begin{align*} \mathbb{E}[N_ {10}|x] &= \mathbb{E}[\sum_{i=1}^mI(\theta_i = 0,\delta_i=1)|x] \\ &= \sum_{i=1}^m\mathbb{E}[I(\theta_i = 0,\delta_i=1)|x] = \sum_{i=1}^m Pr[I(\theta_i = 0,\delta_i=1)|x] \\ &= \sum_{i=1}^mPr(\theta_i=0|x)I(\delta_i=1) \end{align*}\]

비슷하게 그룹 $g$까지 때 $N_{10}$의 조건부 기댓값은 다음과 같다.

\[\mathbb{E}[N_{10}|x,g] = \sum_{i=1}^{m_k} Pr(\theta_{ki}=0|x_{ki})I(\delta_{ki}=1)\]

Efron (2008)

p-value를 사용하는 독립의 $N$개의 검정에 대해서는 각각의 검정마다 $p_i \leq \alpha/N$이 되도록 엄격한 검정이 필요하였다. Fdr을 사용한 검정에서는 이러한 엄격한 기각역이 필요하지 않다.

이를 베이지안 관점에서 설명해보자. 확률변수 $(G,\theta, Z)$; $G$는 해당 관측값이 속하는 그룹, $\theta$는 실제로 null/non-null인지의 지시함수, $Z$를 기각여부를 결정하는 통계량이라고 하자.

베이지안 관점에서 그룹 $k$에 대해 Fdr은 다음과 같다.

\[Fdr_k(z)= Pr(\theta=0|G=k,Z\leq z)\]

이제 각 그룹 $k$마다 cut off $\alpha$에 threshold $z(k)$; 즉 $Fdr_k(z(k)) = \alpha$인 $z(k)$를 잡아서 이보다 작으면, 기각을 하도록 decision rule $\mathcal{R}$을 정하여 이를 $\hat{\delta}$라고 하자.;$Z > z(K)$이면, $\delta = 0$ (null)와 같이 일반화하여 나타낼 수 있다.; 각각의 그룹마다 이를 수행하므로,

\[Fdr_k(\mathcal{R}) = Pr(\theta=0|\delta=1,G=k) = \alpha\]

모든 샘플에 대해서 Fdr을 계산해도, 전체 확률의 법칙에 따라 이는 $\alpha$이다.

\[\begin{align*} Fdr(\mathcal{R}) &= Pr(\theta=0|\delta=1) \\ &=\int Pr(\theta =0|Z\leq z(G), G=k)Pr(k|Z\leq z)dk \\ &= \int \alpha \cdot Pr(k|Z\leq z)dk = \alpha \cdot \int Pr(k|Z\leq z)dk = \alpha \end{align*}\]

Note. 그룹별 $Fdr_k$가 $\alpha$가 되는 threshold를 잡아도, 전체 FDR은 $\alpha$가 되지만, 이는 유일성을 보장하지는 않는다. 따라서 최적의 조합인지는 불분명하다.

Pooled FDR analysis (PLfdr procedure)

모든 관측은 null/non-null간의 mixture의 동일한 분포를 따른다고 가정한다.

\[f = \sum_k \pi_k[(1-p_k)f_{k0} + p_1f_{k1}] = (1-p)f_{0}^* + pf_1^*\]

다음의 통계량을 이용하여 검정을 수행한다.

\[\text{Reject all } H_{(i)}, \ i=1,...,l, \text{ where } l = \max \{ i : \frac{PLfdr_{(1)}+...PLfdr_{(i)}}{i} \leq \alpha \}\]

• $PLfdr = (1-p)f_0^* / f$로 위의 $Lfdr$과 같다. 즉, 모든 그룹의 귀무분포가 $F_0^*$를 따른다는 가정에서 유효하다.

PLfdr은 그룹 정보를 모를 때의 사후확률로 볼 수 있다.

\[\begin{align*} Pr(\theta_i|x_i) &= \sum_k Pr(\theta_i|g_i=k, x_i)Pr(g_i=k|x_i) \\ &= \sum_k \frac{\pi_k(1-p_k)f_{k0}(x_i)}{\sum_{k'} \pi_{k'}f_{k'}(x_i)} = PLfdr(x_i) \end{align*}\]

즉,

\[\mathbb{E}[N_ {10}|x] =\sum_{i=1}^mPr(\theta_i=0|x)I(\delta_i=1) = \sum_{i=1}^R PLfdr_{(i)}\]

Note. PLfdr 값은 작을수록 해당 가설이 거짓 발견일 확률이 낮다는, 즉 진짜 발견일 가능성이 높다는 것을 의미한다. 따라서 작은 값을 갖는 가설들이 유력한 발견 후보이다.

따라서 그룹 정보를 고려하지 않았을 때 FDR은 다음과 같다.

\[FDR = \mathbb{E}[\frac{1}{R}\mathbb{E}[N_{10}|x]]Pr(R>0) = \mathbb{E}[\frac{1}{R}\sum_{i=1}^m PLfdr_{(i)}]Pr(R>0)\]

Separate FDR analysis (SLfdr procedure)

각 그룹 $k$마다 $m_k$개의 가설에 대해 다음을 수행한다.

\[\text{Reject all } H_{(i)}^k, \ i=1,...,l, \text{ where } l = \max \{ i : \frac{CLfdr_{(1)}^k+...CLfdr_{(i)}^k}{i} \leq \alpha \}\] \[CLFdr^k(x_{ki}) = \frac{(1-p_{k})f_{k0}(x_{ki})}{f_{k}(x_{ki})}, \ i=1,...,m_k, k=1,...,K\]

Cai & Sun (2009)

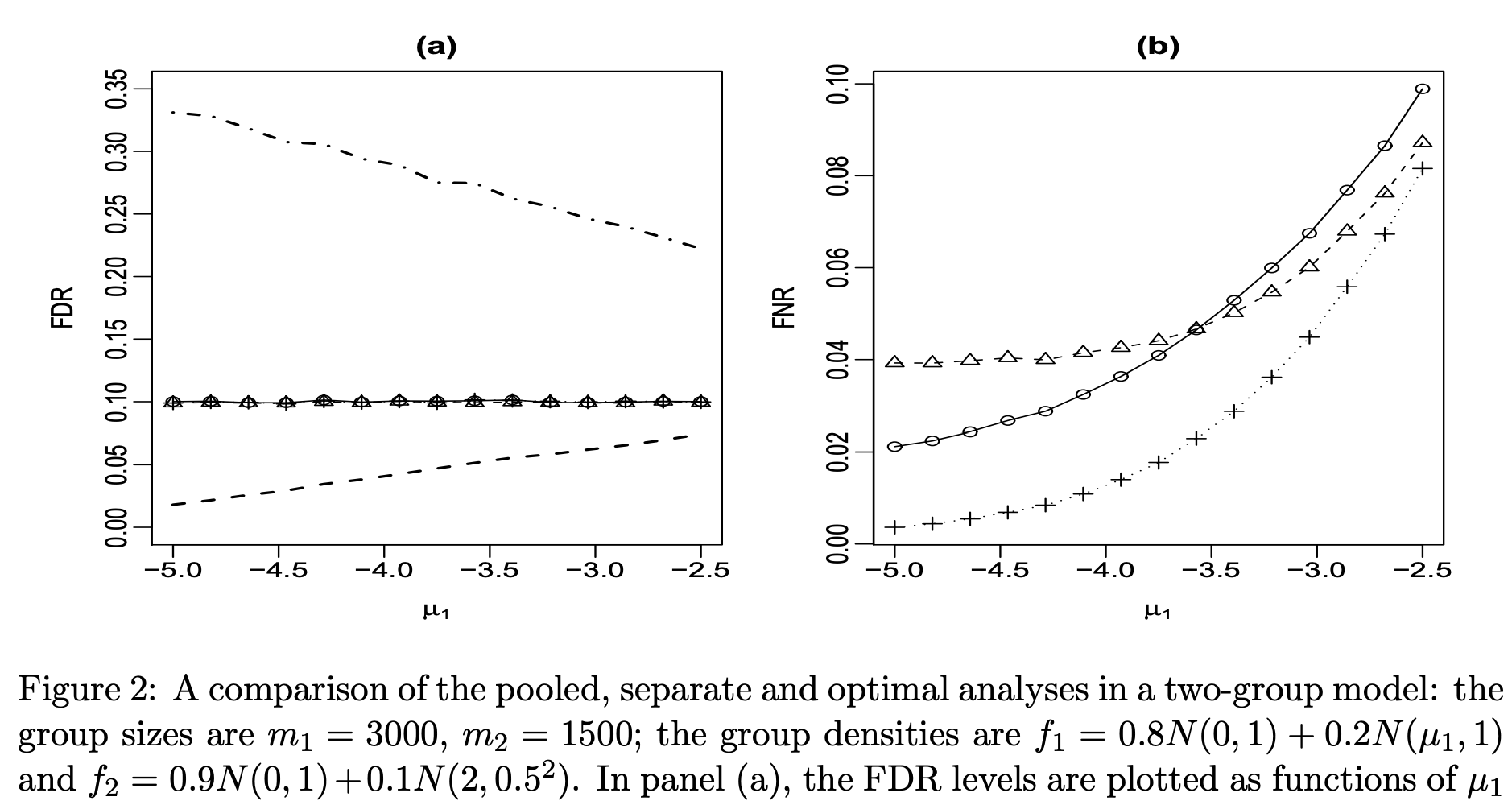
FDR에 대한 통제에 대해서 군집마다 여러개의 가능한 조합들이 존재하고, optimal testing은 이 중 FNR을 최소화하는 검정으로 위 그래프에 +에 대응한다.

CLfdr 통계량에 대해 수준 $\alpha$에서 FDR을 통제하면서 FNR을 최소화하는 검정은 다음과 같다.

\[\delta(CLfdr, c_{OR}(\alpha) \mathbf{1}*m) = (I[CLfdr^k(x*{ki}) < c_{OR}(\alpha) ];i=1,...,m_k,k=1...,K)^T\]

• 즉 optimal cut-off $c_{OR}(\alpha)$가 모든 그룹에 대해서 동일하다.

마찬가지로, optimal cut-off를 직접 계산하는 대신 다음과 같은 근사를 통해 검정을 수행한다.

CLfdr procedure

1. 모든 $CLfdr^k(x_{ki})$를 구하고, $CLfdr_{(1)} \leq … \leq CLfdr_{(m)}$이 되도록 정렬한다. ( $m=\sum_k m_k$)
2. $l = \max { i : \frac{CLfdr_{(1)}+…CLfdr_{(i)}}{i} \leq \alpha }$을 구하고, $H_{(1)},…,H_{(l)}$을 기각한다.

각 그룹별로는 다른 density를 데이터로부터 추정하고, cut-off에 대해서는 모든 그룹에 대해서 같은 값을 사용하기에 pooled/seperate의 하이브리드로 볼 수 있다.

각 그룹의 특성에 맞춰 서로 다른 FDR 수준을 갖고, 그룹 $k$에 대한 FDR의 추정량; $\hat{FDR}^k$는 다음과 같이 해당 그룹에서 기각된 $CLfdr$의 평균으로 계산할 수 있다.

\[\hat{FDR}^k = \frac{1}{R_k}\sum_{i=1}^{R_k}CLfdr^k_{(i)}\]

• $R_k$는 그룹 $k$에서 기각된 가설의 수

random mixture model을 가정할 때, CLfdr procedure은 위 검정들과 마찬가지로, 전체 FDR을 수준 $\alpha$로 통제가 가능하다.

Barber & Ramdas (2017)

Benjamini-Hochberg (BH) procedure

Lfdr procedure와 유사하며, p-value를 사용하여 FDR을 통제한다.

1. $n$개의 가설에 대한 p-value $P=(P_1,…,P_n)$을 계산하여 $P_{(1)} \leq … \leq P_{(n)}$ 이 되도록 정렬한다.
2. FDR 수준을 $\alpha$로 통제한다고 하면, $l = \max{k:nP_{(k)} \leq k \alpha}$을 계산하여 $H_{(1)},…, H_{(l)}$을 기각한다.

Simes p-value

여러 개의 귀무가설 전체가 참인지, 즉 전체 귀무가설(global null hypothesis)을 검정하기 위한 방법이다.

Simes 검정에서 귀무가설은 “$H_1,…,H_n$은 참이다”이다.

\[Simes(P) = \min_k P_{(k)}n/k\]

유의 수준 $\alpha$하에서 귀무가설을 기각할 수 있다.

다음은 유의수준 0.2 하에 20개 p-value에 대해 BH 절차, 그룹별 4개의 Simes p-value 계산한 결과이다.

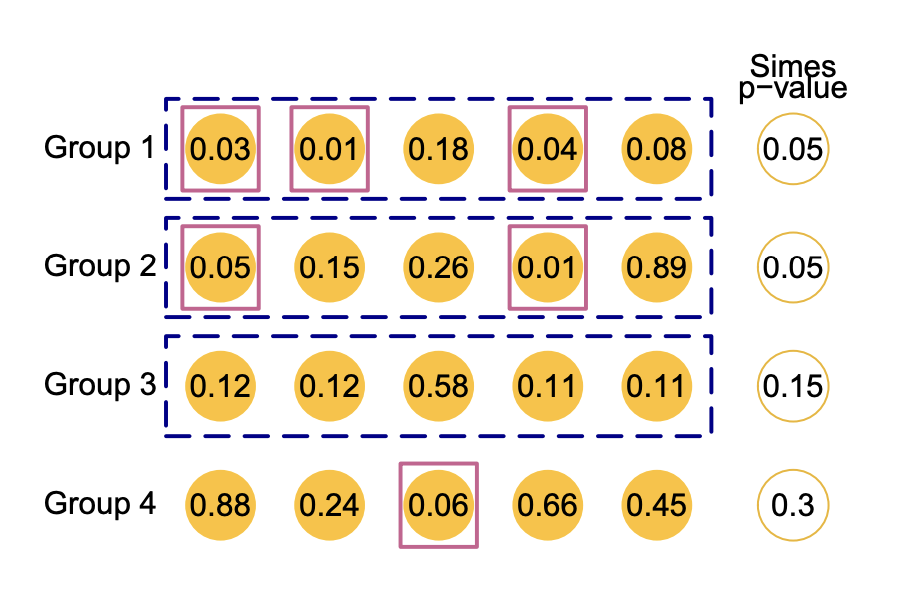
• Group 3: 그룹 수준에서는 유의미하다고 발견되었지만(Simes test), 이 그룹 내의 어떤 p-value도 개별 수준에서는 발견되지 않음(BH 절차).
• Group 4: 그룹 수준에서는 발견되지 않았지만(Simes test), 그룹 내 p-value 중 하나(0.06)가 개별 수준에서는 발견(BH 절차)

즉, 두 절차를 독립적으로 적용할 때 논리적 모순이 발생할 수 있다.

p-filter

위 두개의 절차를 threshold-pair $(t_{ov}, t_{grp}) \in [0,1] \times [0,1]$고려하여 검정을 수행한다.

• $\hat{S} = \hat{S}(t_{ov}, t_{grp}) = {i: P_i \leq t_{ov}, Simes(P_{A_{g(i)}} \leq t_{grp})}$, $A_{g(i)}$는 $P_i$를 포함하는 그룹; 즉 개별 발견에 대한 집합
• \(\hat{S}_{grp} = \hat{S}_{grp}(t_{ov}, t_{grp}) = \{g: \hat{S}(t_{ov}, t_{grp}) \cap A_g \neq \emptyset \}\); 최소 하나의 발견을 포함하는 그룹들의 집합

Overall false discovery proportion (FDP)

\[FDP_{ov} = \frac{|\mathcal{H}^0 \cap \hat{S}|}{\max(1,|\hat{S}|)}\]

실제 개별 귀무가설들의 집합 $\mathcal{H}^0$은 알지 못하므로, 분자의 추정량으로 $n\cdot t_{ov}$를 사용한다.

Note. 잘못된 발견의 수는 \(\|\mathcal{H}^0\|\cdot t_{ov}\)이므로, 위 추정량은 이를 과대추정한다. (최악의 경우에 대한 추정값)

group FDP

\[FDP_{grp} = \frac{|\mathcal{H}*{grp}^0 \cap \hat{S}*{grp}|}{\max(1,|\hat{S}_{grp}|)}\]

위와 비슷하게 분자의 추정량으로 $G \cdot t_{grp}$를 사용한다. ($G$는 전체 그룹의 수)

위 2개의 추정량을 사용하여, 개별/그룹별 유의 수준 $(\alpha_{ov}, \alpha_{grp})$하에서 가능한 threshold pair 집합을 다음과 같이 정의하여, 해당 집합 내에서 최적의 pair를 찾는다.

\[\hat{\mathcal{T}}(\alpha_{ov}, \alpha_{grp}) = \{(t_{ov}, t_{grp}) \in [0,1] \times [0,1]: \hat{FDR}*{ov} \leq \alpha*{ov}, \hat{FDR}*{grp} \leq \alpha*{grp}\}\]

optimal pair를 찾는 과정은 아래와 같이 coordinate-wise하게 탐색한다.