z-value 기반 다중검정의 이점과 knockoff filter

귀무 분포와 대립 분포간의 대칭성이 깨질 때, z-value 기반의 검정이 p-value 기반보다 우수함을 보이고, 모든 모수를 알고 있는 oracle에서의 최적의 절차와 이를 추정하는 방법을 알아볼 것이다. 또한, FDR 기반의 다중 검정을 회귀분석에서의 변수 선택법에 적용한 넉오프 필터에 대해서도 알아볼 것이다.

각각 다음을 참고하였다.

• Sun, W. & Cai, T. T. (2007). Oracle and adaptive compound decision rules for false discovery rate control
• Barber, R. F. & Cand`es, E. J. (2015). Controlling the false discovery rate via knockoffs

Oracle and adaptive compound decision rules

수백, 수천 개의 가설을 동시에 검정하는 대규모 다중 검정에서 주된 목표는 수많은 귀무가설들(null cases) 속에서 대립 가설(non-null cases)을 효과적으로 발견하는 것이다. 이 때 발생하는 두 가지 주요 오류 척도는 기각된 가설 중 잘못된 발견의 비율을 나타내는 거짓 발견율(False Discovery Rate, FDR)과, 채택된 가설 중 놓친 발견의 비율을 의미하는 거짓 비발견율(False Nondiscovery Rate, FNR)이다.

\[\begin{align*} \text{FDR} &= \mathbb{E}[\frac{N_{10}}{R}|R>0]Pr(R>0) \\ \text{pFDR} &= \mathbb{E}[\frac{N_{10}}{R}|R>0] \\ \text{mFDR} &= \frac{\mathbb{E}[N_{10}]}{\mathbb{E}[R]} \\ \text{FNR} &= \mathbb{E}\frac{N_{01}}{S}|S>0]Pr(S>0) \end{align*}\]

Genovese and Wasserman(2002)은 적절한 조건하에서, $\text{mFDR} = \text{FDR} + \mathcal{O}(m^{-1/2})$가 성립함을 밝혔다. 따라서 해당 연구에서는 분석의 편의를 위해 FDR, FNR의 근사값인 mFDR, mFNR를 사용한다.

이제, 해당 연구의 목표는 mFDR을 통제하면서 mFNR을 최소화하는 새로운 검정 절차를 제안하며, 이를 위해 먼저 데이터의 실제 확률 분포를 모두 알고 있다는 이상적인 상황을 가정한 오라클 절차(oracle procedure)를 유도 할 것이다.

다중 검정은 다음과 같은 상황을 고려한다.

해당 연구에서는 확률변수변환을 이용하여 $Z_i = \Phi^{-1}(F(T_i))$를 계산하여 z-value 기반으로 오라클 절차에서 다음을 최적화는 결정기준을 찾는 것을 목표로 한다.

\[\min \text{mFNR} \text{ subject to mFDR} \leq \alpha\]

또한 오라클 절차에서 z-value 기반의 절차가 p-value기반의 절차보다 효율적이며, 특히 대립분포가 귀무 분포와 비대칭이 심할수록, 더 성능의 차이가 심함을 보일 것이다.

Compound decision problem

$m$개의 관측 $x=(x_1,…,x_m) \in \Omega$를 이용하여, 미지의 모수 $\theta=(\theta_1,…,\theta_m)\in \Theta$를 한번에 추론하는 문제를 복합 결정 문제(compound decision problem)라고 한다.

모수를 추정하는데에 판단 기준인 결정 기준을 $\delta=(\delta_1,…\delta_m)$라고 하면,

1. $\delta_i(x) = \delta_i(x_i), \ \forall i$; 즉 각각의 추론을 개별로 결정할 수 있으면 결정 기준 $\delta$을 간단(simple)하다고 한다.
2. 어떤 $i$에 대해 $\delta_i(x)$가 $j\neq i$에 의존하면 결정기준 $\delta$는 혼합(compound)되었다고 한다.
3. 임의의 치환 연산자(permutation operator) $\tau$에 대해 $\delta(\tau(x)) = \tau(\delta(x))$를 만족하면 결정기준 $\delta$는 대칭(symmetric)이라고 한다.

혼합 결정 문제를 이용하여 다중검정을 나타내면 다음과 같다.

미지의 모수는 서로 독립인 성공확률이 $p$인 베르누이 시행을 따른다고 가정하고(여기서 $\theta_i=1$는 non-null인 경우이고, $\theta_i=0$는 null인 경우이다.), 조건부 혼합모델 $X_i\mid\theta_i \sim (1-\theta_i)F_0 + \theta_i F_1$로부터 독립인 $m$개의 $X_i$를 관측되고, $\theta_i$는 알 수 없다고 하자.

다중검정 문제는 위양성의 비율을 $\alpha$이하로 통제하며, 최대한 많은 진양성을 찾는 것이 목표이다. 이 때의 결정 기준은 $\delta=(\delta_1,…,\delta_m) \in \mathcal{L}={0,1}^m$의 꼴로 나타내어진다.

여기서는 Genovese and Wasserman (2002)에서와 같이 mFDR을 $\alpha$이하로 통제하면서, mFNR을 최소화하는 $\delta$를 찾는 문제를 다중 검정 문제라고 한다.

한편, 이를 가중분류 문제로 보아서 잘못 판단했을 때의 두가지 경우인, 제 1종오류(거짓 발견, $I(\theta=0)\delta$)과 제 2종 오류(거짓 비발견)간의 상대적인 비를 $\lambda>0$으로 조절하여, 다음과 같은 손실함수 $L_{\lambda}(\theta, \delta)$를 정의하여 기대 손실 함수 $\mathbb{E}[L_{\lambda}(\theta, \delta)]$(classification risk)를 최소화하는 $\delta$를 찾는 문제로 볼 수 있다.

\[L_{\lambda}(\theta, \delta) = \frac{1}{m}\sum_{i=1}^m[\lambda I(\theta_i=0)\delta_i + I(\theta_i=1)(1-\delta_i)]\]

즉, 다중검정 문제는 거짓 발견률이 $\alpha$이하라는 제약 조건 하에서 가장 낮은 거짓 비발견율을 갖는 결정기준을 찾는 문제이고, 가중 분류 문제는 거짓발견과 거짓 비발견으로 정의된 분류 위험 $\mathbb{E}[L_{\lambda}(\theta, \delta)]$를 최소화하는 결정 기준을 찾는 문제이다.

결정기준 $\delta$에 대해서는 통계량 $u(x) = (T_1(x),…,T_m(x))$와 임계값 $c=(c_1,…,c_m)$을 정의하여, 다음과 같이 나타낼 수 있는 결정기준에 대해서만 고려한다.

\[\delta(x) = I(u(x)<c) = (I[T_1(x) < c_1],..., I[T_m(x) < c_m])\]

만약 통계량이 $(T(x_1),…,T(x_m))$로 각각이 개별적이며 모두 같은 함수 $T$를 사용하고, 임계값이 모두 같다면, 이를 통해 나타낸 결정기준 $\delta$은 대칭임을 알 수 있다. 먼저 이러한 경우에 대해서 알아보자.

SMLR 가정

$T(X_i) \sim G= (1-p)G_0 + pG_1$로 정의하고, 이에 대한 확률밀도함수를 $g=(1-p)g_0 + pg_1$라고 하자. 즉, $g_0$은 귀무 확률밀도, $g_1$은 대립 확률밀도 함수이다. 이렇게 나타낼 수 있는 함수 $T$중에 가능도비가 단조성을 가질 때, 즉 $t$가 증가할수록 $g_1(t)/g_0(t)$가 감소하는 함수들만 모아놓은 함수 집합 $\mathcal{T}$를 SMLR class라고 한다.

마찬가지로, $T\in \mathcal{T}$이고 개별 가설마다 임계값이 모두 같은 경우의 결정기준 $\delta$를 SMLR 결정기준이라고 하며, 이를 모아놓은 집합을 $\mathcal{D}_s$로 표기한다.

SMLR가정이 성립하면 다음을 만족한다. (임계값 $c$가 증가한다는 것은 더 많은 가설을 기각함을 의미한다.)

1. 임계값 $c$가 증가함에 따라, 진짜 발견의 확률 $Pr(\theta_i=1|T(x_i) \leq c)$는 단조 감소한다.
2. 거짓 발견율(mFDR)은 임계값 $c$와 기각된 가설 수의 기댓값 $r$에 대해 단조 증가한다.
3. 거짓 비발견율(mFNR)은 임계값 $c$와 기각된 가설 수의 기댓값 $r$에 대해 단조 감소한다.
4. 가중분류 문제에서 임계값 $c$와 이에 따른 $r$은 분류 가중치$\lambda$에 대해 단조 감소한다.

The Oracle Procedure

다음과 같은 혼합 모델을 가정하자.

\[\begin{align*} \theta_i &\overset{\text{iid}}{\sim} Ber(p) \\ X_i|\theta_i &\overset{\text{ind}}{\sim} (1-\theta_i)F_0 + \theta_i F_1 \end{align*}\]

가중분류 문제에서 $\lambda$가 주어졌을 때, SMLR가정하에서 기대손실함수 $\mathbb{E}[L_{\lambda}(\theta, \delta)]$를 최소화하는 최적의 결정기준을 $\Lambda\in \mathcal{T}$ 와 $c(\lambda)$를 이용하여, $\delta^{\lambda} = (I[\Lambda(x_1)< c(\lambda)],…, I[\Lambda(x_m)< c(\lambda)]) \in \mathcal{D}_s$라고 하자.

이 때, 다중검정에서의 임의의 mFDR 제어수준 $\alpha(0<\alpha<1)$에 대응하는 가중분류 문제에서의 파라미터 $\lambda(\alpha)$가 유일하게 존재하며, 이에 대한 가중분류 문제의 최적의 결정기준 $\delta^{\lambda(\alpha)}$는 $\mathcal{D}_s$에서 mFDR을 $\alpha$이하로 통제하는 결정기준 중 가장 작은 mFNR을 갖는다. 즉, SMLR가정 하에서 다중검정 문제에 대한 최적의 결정기준이기도 하다.

다시말해서 통계량의 가능도비가 단조성만 만족한다면, 그 통계량을 기반으로 한 가중 분류 문제의 최적해가 다중 검정 문제의 최적해이다.

만약 $p,f_0,f_1$이 알려진 경우에 결정기준이 어떻게 나타나는지 알아보자.

먼저 사후분포 $\theta|X$는 다음과 같다.

\[Pr(\theta|X) = \prod_{i=1}^m\frac{I(\theta_i=0)(1-p)f_0(x_i) + I(\theta=1)pf_1(x_i)}{f(x_i)}\]

이제 조건부 기댓값의 성질을 이용하여 다음과 같이 분류 위험을 계산할 수 있다.

\[\begin{align*} \mathbb{E}[L_{\lambda}(\theta, \delta)] &= \mathbb{E}[\mathbb{E}[L_{\lambda}(\theta, \delta)]|X] \\ &=\mathbb{E}[\frac{1}{m}\sum_{i=1}^m\sum_{\theta_i=0}^1 Pr(\theta_i|x_i)[\lambda I(\theta_i=0)\delta_i + I(\theta_i=1)(1-\delta_i)|(x_1,...,x_m)]\\ &=\mathbb{E}[\frac{1}{m}\sum_{i=1}^m \frac{\lambda \delta_i(1-p)f_0(x_i) + (1-\delta_i)pf_1(x_i)}{f(x_i)}|(x_1,...,x_m)] \\ &= \mathbb{E}[\frac{1}{m}\sum_{i=1}^m\frac{pf_1(x_i)}{f(x_i)} + \frac{1}{m}\sum_{i=1}^m\frac{\lambda(1-p)f_0(x_i) - pf_1(x_i)}{f(x_i)}\cdot \delta_i |(x_1,...,x_m)]\\ \end{align*}\]

즉, 이를 최소화하기 위해서는 $\lambda(1-p)f_0(x_i) - pf_1(x_i)$가 음수인 부분만을 포함해야할 것이다. 따라서, 분류 위험을 최소화하는 결정기준은 모든 $i$에 대해 $\delta_i = I[\lambda(1-p)f_0(x_i) < pf_1(x_i) ]$를 만족하는 간단한 결정기준이다. 이를 통계량 $\Lambda$와 임계값 $1/\lambda$을 사용하여 $\delta^{\lambda}(\Lambda,1/\lambda)=(\delta_1,…,\delta_m)$로 나타낸다.

\[\delta_i = I[\Lambda(x_i)= \frac{(1-p)f_0(x_i)}{pf_1(x_i)} <\frac{1}{\lambda}], \ i=1,...,m\]

$\delta^{\lambda}$에 대한 기각영역은 다음과 같이 나타낼 수 있다.

\[K=\{x\in \Omega: \lambda (1-p)f_0(x)<pf_1(x)\}\]

또한, $\delta^{\lambda}$에 대한 분류위험은 다음과 같다.

\[\begin{align*} \mathbb{E}[L_{\lambda}(\theta, \delta^{\lambda})] &= \mathbb{E}[\frac{pf_1(X)}{f(X)}] + \mathbb{E}[\frac{\lambda(1-p)f_0(x_i) - pf_1(x_i)}{f(x_i)}\cdot I[\lambda(1-p)f_0(X) < pf_1(X)]]\\ &= p + \int_K [\lambda (1-p)f_0(x)-pf_1(x)]dx =:R_{\lambda}^* \end{align*}\]

실제 적용에서는 $p,f_0,f_1$를 추정하여 추정된 결정기준 $\delta^{\lambda}(\hat{\Lambda},1/\lambda)$를 사용한다.

Note. $Lfdr = (1-p)f_0/f$을 이용하여, $\Lambda = Lfdr/(1-Lfdr)$로 나타낼 수 있다. 이는 $Lfdr$에 대한 단조증가하는 함수임으로 $(\Lambda>c)$꼴의 결정 규칙은 $(Lfdr>c’)$꼴의 결정 규칙과 같다. 즉, $Lfdr$에 대한 임계값을 활용한 검정은 mFDR을 통제하는 절차 중 가장 작은 mFNR을 갖는다.

Note. $Lfdr$에서의 $f_0,f_1$은 검정통계량 $T_i \sim F$에 대해 $z_i=\Phi^{-1}(F(T_i))$의 확률변수변환 후에 $z_i$에 대한 귀무분포와 대립분포이다.

이제 $Lfdr$ 통계량을 최적의 검정 통계량(oracle test statistic)이라고 하고, $T_{OR}(Z_i) = (1-p)f_0(Z_i)/f(Z_i)$이라 표기하자. 이제 임계값 $\lambda$에 대해 최적의 결정기준 $\delta(T_{OR},\lambda) = (\delta_1,…,\delta_m)$은 다음과 같다.

\[\delta_i = I[T_{OR}(Z_i) < \lambda], i=1,...,m\]

이제 mFDR을 유도하기 위해 $T_{OR}(Z_i)$에 대해 다음과 같은 혼합 분포를 가정한다.

\[T_{OR}(Z_i) \sim G_{OR}(\lambda)=(1-p)G_{OR}^0(\lambda) + pG_{OR}^1(\lambda)\]

mFDR은 다음과 같다.

\[\begin{align*} \alpha \geq \text{mFDR} &= \frac{\mathbb{E}[\sum_{i=1}^mI(\theta_i=0, \delta_i=1)]}{\mathbb{E}[\sum_{i=1}^mI(\delta_i=1)]} \\ &= \frac{\sum_{i=1}^mPr(\delta_i=1|\theta_i=0)Pr(\theta_i=0)}{\sum_{i=1}^mPr(\delta_i=1)} \\ &= \frac{(1-p)G_{OR}^0(\lambda)}{G_{OR}(\lambda)} =:Q(\lambda) \end{align*}\]

한편, $T_{OR} \in \mathcal{T}$로 SMLR을 따른다고 가정하면, $Q(\lambda)$는 단조증가한다. 또한, SMLR가정에 의해 mFNR은 이에 대해 단조감소함으로 최적의 임계값은 $\lambda_{OR}=Q^{-1}(\alpha)$이다.

Note. $\tilde{G}(\lambda) = 1-G_{OR}(\lambda)$라고 하면, $\alpha$이하의 mFDR에 대해 가장 작은mFNR은 아래와 같다.

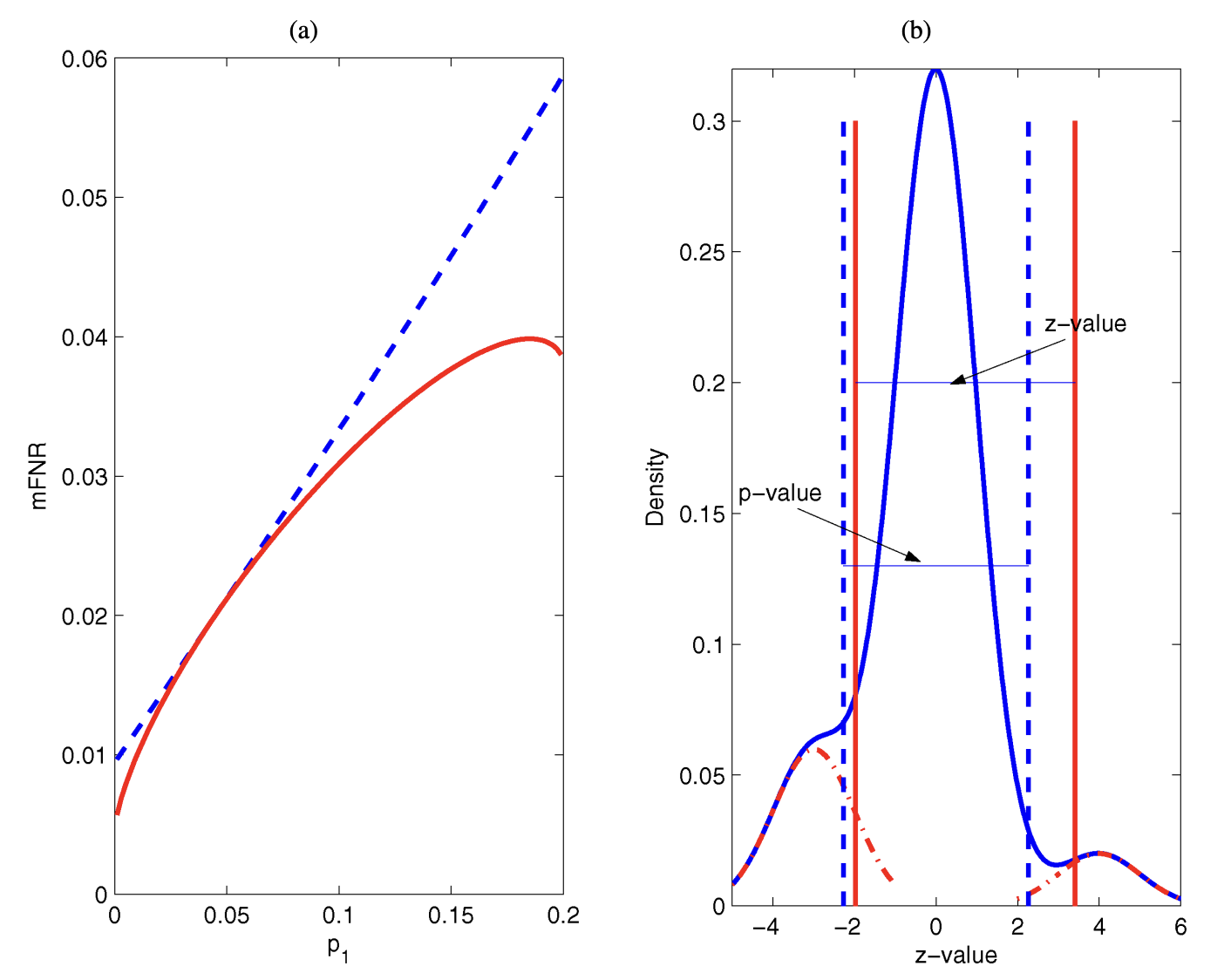
\[\frac{p\tilde{G}^1(\lambda_{OR})}{\tilde{G}(\lambda_{OR})} =\tilde{Q}_{OR}(\lambda_{OR})\]

p-value는 보통 양측 검정에서 에서 $2(1-\Phi(|z_i|))$와 같이 계산된다. 이 과정에서 z-value의 부호 정보가 사라지고 절댓값만 남는다. 따라서 대립 분포가 $\mathcal{N}(\mu,\sigma^2)$이던지, $\mathcal{N}(-\mu, \sigma^2)$던지 p-value의 대립분포는 완전히 같다. 즉 대립 분포의 효과의 크기는 알지만, 방향성은 알 수 없다는 문제가 있으며 항상 대칭적인 기각역을 설정하기에, 귀무분포와의 비대칭성이 존재하는 경우, 비효율적인 방식이다.

하지만, z-value기반의 경우 크기와 방향을 모두 포함하는 $z_i$로부터 검정통계량의 확률분포를 가정하기에 $G$는 이러한 비대칭성을 반영할 수 있다. 이로부터 비대칭서이 반영된 mFDR $Q$가 계산되고, 다시 $Q$를 이용하여 최적의 임계값 $\lambda_{OR}$를 구하기에, z-value 기반의 절차의 기각역은 대립과 귀무간의 비대칭성을 반영할 수 있기에 자연스럽게 같은 mFDR하에서도 더 나은 mFNR을 얻을 수 있다고 생각해볼 수 있다.

Adaptive procedure

오라클 절차를 수행하기 위해서는 $T_{\text{OR}}(z)$의 분포를 구해야 하지만 이에 대한 계산은 매우 복잡하다. 반면 z-value는 normal mixture를 따르기에, z-value의 추정만 필요한 적응적 절차(adaptive procedure)를 수행한다.

$m$개의 가설들에 대응하는 검정통계량으로부터 구한 z-value $z_1,…,z_m$가 $Z_i \overset{\text{ind}}{\sim} (1-p)F_0 + p F_1$로부터의 normal mixture를 따를 것이라 가정한다.

일반적으로 $Z_i \sim (1-p)\mathcal{N}(\mu_0,\sigma_0^2) + p\mathcal{N}(\mu_i,\sigma_i^2)$이고 대립가설의 모수$\ (\mu_i,\sigma^2_i)$는 어떤 이변량 확률분포 $F(\mu,\sigma^2)$를 따를것이라 가정한다.

이제 $F_0,F_1$의 확률밀도함수를 각각 $f_0,f_1$이라고 하면 $T_{\text{OR}}$은 다음과 같다.

\[T_{OR}(z_i) = Lfdr(z_i)=(1-p)f_0(z_i)/f(z_i), \ i=1,...,m\]

$p,f_0,f$에 대한 일치추정량을 \(\hat{p}, \hat{f}_0, \hat{f}\)을 통해, \(T_{\text{OR}}(z_i)\)의 추정량 $\hat{T}_{\text{OR}}(z_i)$을 구한다.

\[\begin{align*} \hat{T}_{OR}(z_i) &:= \min((1-\hat{p})\hat{f}_0(z_i)/\hat{f}(z_i),1)\\ &=\hat{Lfdr}(z_i) \\&\text{ where } \hat{p} \xrightarrow{p}p, \mathbb{E}\|\hat{f}-f\|^2 \rightarrow 0, \mathbb{E}\|\hat{f}_0-f_0\|^2 \rightarrow 0 \end{align*}\]

임계값 $\lambda_{\text{OR}}$의 추정량도 비슷하게 다음과 같이 구할 수 있다.

\[\begin{align*} Q_{\text{OR}}(\lambda)&=\frac{(1-p)G_{OR}^0(\lambda)}{G_{OR}(\lambda)} \\&= \frac{(1-p)Pr[T_{\text{OR}}(Z) <\lambda\mid \text{null}]}{Pr[T_{\text{OR}}(Z)<\lambda]} \\ &= \frac{\int I[T_{\text{OR}}(z) < \lambda]T_{\text{OR}}(z)f(z)dz}{\int I[T_{\text{OR}}(z) < \lambda]f(z)dz} \\ &\approx \frac{\sum_{i=1}^m I[\hat{T}_{\text{OR}}(z_i) < \lambda]\hat{T}_{\text{OR}}(z_i)}{\sum_{i=1}^m I[\hat{T}_{\text{OR}}(z_i) < \lambda]}=:\hat{Q}_{\text{OR}}(\lambda)\\ \hat{\lambda}_{\text{OR}} &:= \sup\{t\in(0,1): \hat{Q}_{\text{OR}}(t) \leq \alpha \} \end{align*}\]

이를 이용한 결정 규칙 \(\delta(\hat{T}_{\text{OR}}, \hat{\lambda}_{\text{OR}})\)은 $T_{\text{OR}}$에 대한 SMLR 가정하에 다음이 성립한다.

1. \(\delta(\hat{T}_{\text{OR}}, \hat{\lambda}_{\text{OR}})\)은 무한 표본에 대해서 mFDR을 $\alpha$이하로 통제한다.
2. \(\delta(\hat{T}_{\text{OR}}, \hat{\lambda}_{\text{OR}})\)은 무한 표본에 대해서 \(\tilde{Q}_{OR}(\lambda_{OR}) + o(1)\)이다.

다시말해서, 표본의 수가 무한히 많아지면 $\delta(T_{\text{OR}}, \lambda_{\text{OR}})$와 같은 성능을 보인다.

이에 대한 증명은 (Sun, W. & Cai, T. T. ,2007)의 appendix를 참조.

이제 \(\hat{\lambda}_{\text{OR}}\)를 구하기 위해 $\hat{Q}_{\text{OR}}$의 변화가 일어나는 지점인 관측한 $m$개의 $\hat{Lfdr}_i$들만을 임계값으로 고려한다.

\[\hat{Q}_{\text{OR}}(\hat{Lfdr}_{(k)}) = \frac{1}{k}\sum_{i=1}^k \hat{Lfdr}_{(i)} \text{ where } \hat{Lfdr}_{(1)} \leq ... \leq \hat{Lfdr}_{(m)}\]

또한 $\hat{Q}_{\text{OR}}$가 변화되는 지점은 정렬된 통계량의 누적평균임으로, 단조증가함을 알 수 있다. 즉, 다음이 성립한다.

\[\hat{\lambda}_{OR}= \hat{Lfdr}_{(k)} \text{ where } k=\max\{1\leq i \leq m: \hat{Q}(\hat{Lfdr}_{(i)})\leq \alpha\}\]

따라서, 이에 대응하는 가설 $H_{(1)},…,H_{(m)}$에 대하여 다음과 같은 절차를 제안한다.

\[\begin{align*} &\text{reject } H_{(1)},...,H_{(k)} \\ &\text{where } k = \max\{1\leq i \leq m:\frac{\sum_{j=1}^i \hat{Lfdr}_{(j)}}{i} \leq \alpha\} \end{align*}\]

Knock-off filters

선형모델에서 FDR을 통제하는 변수 선택방법이다. 노이즈에 대한 사전지식, 회귀 계수의 스케일, 변수의 수등을 고려하지 않아도 유한개의 샘플을 통해서도 FDR 통제가 가능하다. $n$개의 샘플과 $p$개의 변수에 대해 고정된 $\mathbf{X} \in \mathbb{R}^{n \times p}$와 반응변수 $\mathbf{y} \in \mathbb{R}^n$에 대해 회귀계수 $\mathbf{\beta} \in \mathbb{R}^p$을 통해 다음의 선형 모델을 가정하다.

\[\mathbf{y} = \mathbf{X}\mathbf{\beta} + \mathbf{z} \text{ where } \mathbf{z} \sim \mathcal{N}_p(0,\sigma^2I)\]

여기서 $\mathbf{X}$는 정규화를 거친 행렬로, 표본공분산 행렬을 $\Sigma = X^TX$로 정의한다. ( $\Sigma_{jj} = 1, \ j=1,…,p$).

이제 $H_j:\beta_j=0$에 대한 $p$개의 가설을 검정한다. 이를 통해 선택된(또는 기각된 가설에 대응하는) 변수들의 인덱스 집합을 $\hat{S} \subset {1,…,p}$라고 하면, $\hat{S}$에 대한 FDR은 다음과 같이 정의한다.

\[\text{FDR} = \mathbb{E}[\text{FDP}] = \mathbb{E}_{\mathbf{z} \sim \mathcal{N}_p(0,\sigma^2I)}[\frac{\#\{j: \beta_j=0, j \in \hat{S}\}}{\max(\#\{j: j \in \hat{S}\},1)}]\]

넉오프 필터는 실제 데이터와 공분산 구조가 완전히 같으면서 실제 각각의 변수들과는 상관관계가 작은 가짜 데이터 $\tilde{\mathbf{X}} \in \mathbb{R}^{n \times p}$를 만들어 $2p$개의 실제 변수, 가짜 변수 쌍을 기반으로 적절한 검정통계량을 구하고, 데이터 기반으로 계산된 임계값을 기각역으로 가설을 검정하는 방법이다.

이러한 실제 변수와 넉오프 필터 쌍은 FDR을 구하는데 있어서 실제 발견은 $X_j$에 대응하고, 가짜 발견은 $\tilde{X}_j$에 대응할 것이라 자연스럽게 예상해볼 수 있다.

넉오프 필터는 $n\geq 2p$와 더 나아가 $p < n < 2p$인 경우에도 적용이 가능하다.

양의 값을 갖는 벡터 $\mathbf{s} \in \mathbb{R}_+^p$에 대해 $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} \in \mathbb{R}^{n \times 2p}$는 다음을 만족해야한다.

\[\begin{pmatrix} \mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T \begin{pmatrix} \mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} = \begin{pmatrix} \Sigma & \Sigma - diag(\mathbf{s}) \\ \Sigma - diag(\mathbf{s}) & \Sigma \end{pmatrix} =: \mathbf{G} \succeq 0\]

여기서 $\mathbf{G} \succeq0$에 대한 필요충분조건은 $\Sigma\succeq0$이고 슈어의 보수 행렬이 양의준정부호 즉, $\Sigma - (\Sigma - diag(\mathbf{s}))^T\Sigma^{-1}(\Sigma - diag(\mathbf{s})) \succeq 0$여야 한다. $\Sigma \succeq0$임은 모델 가정에 의해 성립함으로 슈어의 보수 행렬 조건을 정리한 $2\Sigma \succeq diag(\mathbf{s})$를 만족해야 한다.

즉, 모든 $i,j$에 대해 $X_i^TX_j = \tilde{X}_i^T\tilde{X}_j$이고 심지어, $i\neq j$이면 $\tilde{X}_i^TX_j$인 기존의 공분산 구조를 완전히 모방하는 행렬 $\tilde{X}$를 만드는 것이다.

단, 검정력을 키우기 위해 실제 변수 $X_j$와는 최대한 상관관계가 작아지도록 \(\tilde{X}_j\)들을 구성한다. 즉 변수 $j$마다 \(X_j^T\tilde{X}_j = \Sigma_{jj}-s_j = 1-s_j\)는 0에 가깝도록하는 $\mathbf{s} \in \mathbb{R}_+^p$를 찾아야한다. 이에 대해서는 다음의 두가지 방법을 고려해볼 수 있다.

첫번째로는 간단하게, 모든 $j$마다의 상관관계 $X_j^T\tilde{X}_j$가 같다는 제약 하에서 최적의 $\mathbf{s}$를 구하는 방법이 있다.

\[\min_s (1-s) \text{ subject to } 2\Sigma-sI \succeq 0, 0\leq s \leq 1\]

행렬이 양의 준정부호이기 위한 필요충분조건은 모든 고윳값이 음이 아님을 의미하기에, $\Sigma$의 가장 작은 고윳값을 $\Sigma_{\text{min}}$라고 하면, 첫번째 제약조건은 $2\Sigma_{\text{min}}-s \geq 0$임으로 $0 \leq s \leq \min(1,2\Sigma_{\text{min}})$으로 제약조건을 다시 쓸 수 있다. 즉, 모든 실제와 넉오프변수 상관관계는 \(X_j^T\tilde{X}_j = 1-\min(2\Sigma_{\text{min}},1)\)로 같다.

두번째로는 실제변수와 넉오프변수의 상관관계의 평균을 최소화하는 방법이다.

\[\min_{\mathbf{s}} \sum_{j=1}^p(1-s_j) \text{ subject to } 2\Sigma \succeq diag(\mathbf{s}), 0\leq s_j \leq 1 \ \forall j\]

이는 준정부호 계획법(semidefinite program, SDP)을 사용하여 효율적으로 구할 수 있다. 이는 개별 $j$마다 $s_j$를 최대로하기에, 일반적으로 첫번째 방법보다 검정력을 높일 수 있다.

일반적인 경우($n\geq 2p$)

이제 벡터 $\mathbf{s}$를 구했으면, 다음과 같이 $\tilde{\mathbf{X}}$를 구할수 있다.

먼저, $p \leq 2n$이기에 $n$차원 벡터공간에서 $col(\mathbf{X})$와 직교하는 부분공간을 만들 수 있다. 이러한 정규직교기저행렬을 $\tilde{\mathbf{U}} \in \mathbb{R}^{n \times p}$라고 하자. (즉, $\tilde{\mathbf{U}} ^T\mathbf{X} = \mathbf{0}$) 또한, $\mathbf{G}$는 양의 준정부호이기에 $\mathbf{C}^T\mathbf{C} = 2diag(\mathbf{S}) - diag(\mathbf{S})\Sigma^{-1}$의 촐레스키 분해가 가능하다. 이제 다음과 같이 $\tilde{\mathbf{X}}$를 정의하면 이는 위에서 $\mathbf{G}$의 정의를 만족한다.

\[\tilde{\mathbf{X}} = \mathbf{X}( I - \Sigma^{-1} diag(s)) + \tilde{\mathbf{U}}\mathbf{C}\]

고차원 데이터의 경우 ($p < n < 2p$)

$n <2p$이기에 기존 $n$차원 벡터공간에서 $col(\mathbf{X})$와 직교하는 부분공간을 만들 수 없다. 이 경우 $2p$차원의 벡터공간에서의 $col(\mathbf{X})$와 직교하는 부분공간을 사용하기 위해, $\mathbf{X}$의 각 컬럼벡터에 $(2p-n)$의 영벡터를 증강한$\begin{pmatrix} \mathbf{X}^T &\mathbf{0^T}\end{pmatrix}^T \in \mathbb{R}^{2p \times p}$에 대한 넉오프 필터를 계산한다. 이 때 증강된 샘플들에 대응하는 반응변수 $\mathbf{y}’ \sim \mathcal{N}_{2p-n}(0, \sigma^2)$을 따르도록 샘플링을 진행해야하기에 $\sigma$에 대한 추정이 필요하다. 또한, 전체 반응변수는 다음을 따른다.

\[\begin{pmatrix} \mathbf{y} \\ \mathbf{y}'\end{pmatrix} \sim \mathcal{N}_{2p}(\begin{pmatrix} \mathbf{X} \\ \mathbf{0}\end{pmatrix}\beta, \sigma^2I)\]

검정통계량

이후 유한개의 샘플에서의 FDR통제를 만족하기 위한 통계량은 다음과 같다.

각 가설들에 대해 기각역은 $W_j \geq t(t>0)$의 꼴로 $W_j$가 큰 양수값을 갖을수록 대립가설 $\beta_j\neq0$을 지지하도록하는 통계량 $\mathbf{W}(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} , \mathbf{y}) \in \mathbb{R}^p$를 다음의 충분성, 반대칭성 성질을 만족하도록 구성한다.

충분성

통계량 $\mathbf{W}$가 오직 증강행렬의 표본 공분산 $\mathbf{G}$와 반응변수와의 내적 $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} ^T \mathbf{y}$에만 의존할 때 충분성을 만족한다고 한다. 즉, 양의 준정부호인 $2p \times 2p$행렬들의 집합을 \(S_{2p}^+\)라고 할때, 다음을 만족하는 함수 \(f:S_{2p}^+\times \mathbb{R}^{2p} \rightarrow \mathbb{R}^p\)가 존재한다.

\[\mathbf{W} = f(\begin{pmatrix} \mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T \begin{pmatrix} \mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}, \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} ^T \mathbf{y})\]

즉, 충분성을 만족하는 통계량에 대해 $f$가 주어졌을 때, $\mathbf{W}_1 \overset{d}{=} \mathbf{W}_2$를 보이기 위해서는 위 두 인자가 같음을 보이면 충분하다.

반대칭성

통계량 $\mathbf{W}(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} , \mathbf{y}) =(W_1,…,W_p)$에 대해 $X_j$와 $\tilde{X}_j$를 뒤바꾸면 $W_j$는 부호가 바뀔 때, 반대칭성을 만족한다고 한다.

즉, $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}$ 와 임의의 부분집합 $S \subset {1,…,p}$에 대해 $j \in S$이면, $X_j$와 \(\tilde{X}_j\)를 뒤바꾼 행렬을 \(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}_{\text{swap}(S)}\)이라고 하면, $\mathbf{W}$는 다음을 만족해야 한다.

\[W_j(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}_{\text{swap}(S)}, \mathbf{y}) =\begin{cases} W_j(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} , \mathbf{y}) & \text{ if } j \notin S \\ -W_j(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} , \mathbf{y}) & \text{ if } j \in S \end{cases}\]

가설 검정을 하는데에 있어서, $W_j$가 큰 양의 값을 갖을 때, $\beta_j \neq 0$을 지지하고, 실제 발견은 $X_j$에 대응하고, 가짜 발견은 $\tilde{X}_j$에 대응하도록 하여, 임계값 $t$에 대해 FDR을 계산하는데에 있어서 실제 발견을 $W_j \geq t$, 가짜 발견을 $W_j \leq -t$라고 한다면, 반대칭성은 FDR 제어를 위해 만족해야하는 자연스러운 성질일 것이다.

예시

라쏘 모델을 사용하여 충분성, 반대칭성을 만족하는 통계량을 구할 수 있다. 먼저 모든 변수가 선택되지 않는 $\lambda = \infty$부터 $0$까지 다음을 만족하는 $\hat{\beta}(\lambda)$를 계산하여 라쏘 경로를 구한다.

\[\begin{align} \hat{\beta}(\lambda) &= \underset{\mathbf{b}}{\text{argmin}} [\frac{1}{2}\text{RSS}(b) + \lambda\|\mathbf{b}\|_1 ] \\ &= \underset{\mathbf{b}}{\text{argmin}} [\frac{1}{2} \mathbf{b}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}\mathbf{b}^T - \mathbf{b}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} \mathbf{y}+ \lambda\|\mathbf{b}\|_1 ] \\ &= \underset{\mathbf{b}}{\text{argmin}} f(\mathbf{b};\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}, \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\mathbf{y},\lambda) \end{align}\]

라쏘경로의 $\lambda$축에서 $X_j$가 선택되는 지점은 $Z_j = \sup{\lambda:\hat{\beta}_j\neq0}(j=1,…,2p)$이다. 이제, 검정 통계량 $\mathbf{W}$를 다음과 같이 정의하자. 이는 반대칭을 만족하면서, 실제 변수가 넉오프 변수보다 먼저 변수집합에 들어왔을 때는 가설이 기각되고, 반대로 넉오프 변수가 먼저 들어왔을때는 기각을 못하도록 한다.

\[W_j = \begin{cases} \max(Z_j,Z_{j+p}) & \text{if } Z_j> Z_{j+p} \\ -\max(Z_j,Z_{j+p}) & \text{if } Z_j< Z_{j+p} \\ 0 &\text{if } Z_j= Z_{j+p} \end{cases}, \ j=1,...,p\]

또는 실제 변수와 넉오프 변수를 구별하여 $(Z_1,…,Z_p, \tilde{Z}_1,…,\tilde{Z}_p)$로 표기하여 다음과 같이 나타낼 수 있다.

\[W_j = sgn(Z_j-\tilde{Z}_j) \cdot \max(Z_j,\tilde{Z}_j) , \ j=1,...,p\]

위의 최적해 $\hat{\beta}(\lambda)$는 $\lambda$가 고정되었을 때, $(\mathbf{X}^T\mathbf{X}, \mathbf{X}^T\mathbf{y})$에 대한 함수임으로 충분성을 만족한다. 또한, $W_j$의 정의에 의해 자연스럽게 반대칭성 또한 만족한다.

기각역 (임계값)

임계값 $t(t>0)$를 사용하여 $W_j \geq t$의 기각역을 통해 유의한 변수들을 모아놓은 인덱스 집합 $\hat{S}={j: W_j \geq t }$에 대한 FDP는 다음과 같다.

\[\text{FDP}(t) = \frac{\#\{j: \beta_j=0, W_j \geq t\}}{\max(\#\{j: W_j \geq t \},1)}\]

FDR 제어수준을 $q$라고 하면, 데이터 기반의 임계값 $T$는 $\mathbf{W}$의 크기에 대한 집합 $\mathcal{W} = {|W_j|:W_j \neq 0,j=1,…,p}$을 이용하여 다음과 같이 정의한다.

\[T = \min \{t \in \mathcal{W} : \hat{\text{FDP}}(t)\leq q\} \text{ where } \hat{\text{FDP}}(t)=\frac{\#\{j: W_j \leq -t\}}{\max(\#\{j: W_j \geq t\},1)}\]

위 임계값을 사용한 절차를 넉오프 방법(knockoff method)이라고 한다. 또다른 데이터기반의 임계값은 다음과 같다.

\[T = \min \{t \in \mathcal{W} : \frac{1+\#\{j: W_j \leq -t\}}{\max(\#\{j: W_j \geq t\},1)} \leq q\}\]

분자에 1이 더해져 넉오프 방법보다 더 보수적인 임계값으로 이는 넉오프+ 방법(knockoff+ method)이라고한다.

(만약 $\hat{\text{FDP}}(t)\leq q$를 만족하는 $t \in \mathcal{W}$가 존재하지 않는다면, 어떠한 가설도 기각하지못하도록 $T = \infty$로 둔다.) 여기서 $\hat{\text{FDP}}(t)$는 FDP의 넉오프 추정량이라고 한다. 넉오프 추정량에 대한 다음의 근사를 통해 $T$를 사용한 변수선택 절차는 FDP를 통제함을 보일 수 있다.

\[\begin{align*} \text{FDP}(t) &= \frac{\#\{j: \beta_j=0, W_j \geq t\}}{\max(\#\{j: W_j \geq t \},1)} \\ &\approx \frac{\#\{j: \beta_j=0, W_j \leq -t\}}{\max(\#\{j: W_j \geq t \},1)} \\ &\leq \frac{\#\{j: W_j \leq -t\}}{\max(\#\{j: W_j \geq t\},1)} \}=\hat{\text{FDP}}(t) \end{align*}\]

위의 근사가 가능하려면, 임의의 임계값 $t$에 대해 다음을 만족해야한다.

\[\begin{align} \#\{j: \beta_j=0, W_j \geq t\} &\overset{d}{=} \#\{j: \beta_j=0, W_j \leq -t\} \\ \#\{j: \beta_j=0, |W_j| \geq t, sgn(W_j)=1\} &\overset{d}{=} \#\{j: \beta_j=0, |W_j| \geq t, sgn(W_j)=-1\} \\ \end{align}\]

한편, 귀무가설에 대응하는 인덱스 집합을 $\mathcal{H}_0 = {j:\beta_j=0}$이라고 하면, 충분성과 반대칭성을 만족하는 통계량 $\mathbf{W}$에 대해 $j \in \mathcal{H}_0$이면, $\epsilon_j \overset{\text{i.i.d}}{\sim} {-1,1}$이고, $j \notin\mathcal{H}_0$이면 $\epsilon_j=1$인 통계량 $\mathbf{\epsilon}\in{-1,1}^p$를 정의하면 다음을 만족한다.

\[\begin{align} \mathbf{W}=(W_1,...,W_p) &\overset{d}{=} (\epsilon_1 \cdot W_1,...,\epsilon_p \cdot W_p) \end{align}\]

다시말해서,

\[\{sgn(W_j)\}_{j\in\mathcal{H}_0}\mid\{|W_j|\}_{j=1}^p,\{sgn(W_j)\}_{j \notin \mathcal{H}_0} \overset{\text{i.i.d}}{\sim} \{-1,1\}\]

증명은 다음과 같다. $(\epsilon_1 \cdot W_1,…,\epsilon_p \cdot W_p)$은 귀무가설에 한해서만 몇몇 $W_j$의 부호가 바뀐 통계량이다. 이러한 몇몇 변수들을 인덱스 집합 \(S=S(\mathbf{\epsilon}) = \{j:\epsilon_j=-1\} \subset \mathcal{H}_0\)이라고 정의하자. 이는 반대칭성을 사용하여 위의 $\mathbf{W}$를 구성한 $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}$에서 $S$에 속하는 변수들만 맞바꾼 \(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}_{\text{swap}(S)}\)로 구성한 통계량 $\mathbf{W}_{\text{swap}(S)}$과 같은 분포이다.

\[(\epsilon_1\cdot W_1,...,\epsilon_p\cdot W_p) \overset{d}{=} \mathbf{W}_{\text{swap}(S)}\]

따라서, $\mathbf{W} \overset{d}{=} \mathbf{W}_{\text{swap}(S)}$임을 보이면 충분하다.

이는 충분성 조건에 의해 \(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}=\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}_{\text{swap}(S)}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}_{\text{swap}(S)}\)이고, \(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} ^T \mathbf{y} \overset{d}{=} \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} ^T_{\text{swap}(S)} \mathbf{y}\) 를 만족하면 된다.

첫번째 조건에 대해서는 \(\mathbf{X}^T\mathbf{X} = \mathbf{X}^T_{\text{swap}(S)}\mathbf{X}_{\text{swap}(S)}\)이고, \(\mathbf{X}^T\tilde{\mathbf{X}} = \mathbf{X}^T_{\text{swap}(S)}\tilde{\mathbf{X}} _{\text{swap}(S)}\)를 만족하면 충분하며 $\text{swap}(S)$는 $j\in S$에 대해 $X_j, \tilde{X}_j$를 맞바꾼 것임으로 넉오프 필터의 정의에 의해 이를 만족한다.

두번째 조건에 대해서는 $\mathbf{y} \sim \mathcal{N}_{p}(\mathbf{X}\beta, \sigma^2I)$와 상수 행렬간의 곱이기에, 각각은 정규분포를 따름으로 기댓값과 분산이 같음을 보이면 충분하다.

\[\begin{align*} \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T \mathbf{y} &\sim \mathcal{N}(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix} ^T \mathbf{X}\beta, \sigma^2\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}) \\ \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T_{\text{swap}(S)} \mathbf{y} &\sim \mathcal{N}(\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T_{\text{swap}(S)} \mathbf{X}\beta, \sigma^2\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T_{\text{swap}(S)} \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix})_{\text{swap}(S)} \end{align*}\]

분산에 대해서는 첫번째 조건에서 보였음으로, $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\mathbf{X}\beta = \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T_{\text{swap}(S)} \mathbf{X}\beta$임을 보여야한다.

$\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\mathbf{X}\beta$의 $i$번째 성분은 $\begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\mathbf{X}$의 $i$번째 행과 $\beta$의 곱이다.

\[\begin{align*} \begin{pmatrix}\mathbf{X} & \tilde{\mathbf{X}} \end{pmatrix}^T\mathbf{X} &= \begin{pmatrix}X_1^T \\ \vdots \\ \tilde{X}_p \end{pmatrix} (X_1 \cdots X_p) \in \mathbb{R}^{2p \times p} \\ \end{align*}\]

즉, $i\leq p$이면, $i$번째 성분은 $(X_i^TX_1,…,X_i^TX_p)\beta = \sum_jX_i^TX_j\beta_j$이고 $i>p$이면 $\sum_j \tilde{X}_{i-p}^TX_j\beta_j$이다.

따라서 $i \in S$인 성분에 대해서만 $X_i^TX_1\beta_1+…+X_i^TX_p\beta_p = \tilde{X}_i^TX_1\beta_1 + … + \tilde{X}_i^TX_p\beta_p$임을 확인하면 충분하다. 넉오프 필터의 정의에 의해 $j \neq i$이면, $X_i^TX_j= \tilde{X}_i^TX_j$임으로, $i=j$인 경우인 $X_i^TX_i\beta_i = \tilde{X}_i^TX_i\beta_i$가 만족하는지만 보이면 된다. 한편, $i\in S$이면 $i \in \mathcal{H}_0$임으로 $\beta_i=0$임으로 이를 만족한다.

즉, \(\mathbf{W}\overset{d}{=} \mathbf{W}_{\text{swap}(S)}\)이고 \(\mathbf{W}_{\text{swap}(S)}\overset{d}{=} (\epsilon_1\cdot W_1,...,\epsilon_p\cdot W_p)\) 임으로, $\mathbf{W}\overset{d}{=} (\epsilon_1 \cdot W_1,…,\epsilon_p \cdot W_p)$

가 성립한다.

따라서, $\beta_j=0$이면 $|W_j|$의 여부와 상관없이 부호를 뒤바꿔도 같은 통계량임을 알 수 있음으로 넉오프 추정량에 대한 근사가 성립한다.

다시 말해서, \(\#\{\text{null } j:\mid W_j\mid \geq t\}=N_t\)를 조건부로 하는 \(V^{\pm}(t) = \#\{\text{null }j: \mid W_j\mid \geq t, sgn(W_j) = \pm 1 \}\)의 분포는 $Bin(N_t, 1/2)$를 따른다.

여기에 임계값 $t=0$을 대입하면 $N_0$은 귀무가설이 참인 가설의 수 $p_0=|\mathcal{H}_0|$이고 각각은 전체 귀무가설 중에 부호가 양수인 가설의 수 $V^+(0)$과 음수인 가설의 수 $V^-(0)$가 각각 $Bin(p_0,1/2)$을 따르고, $V^+(0)+V^-(0)=p_0$이다.

knockoff+에서의 FDR통제

먼저 더 보수적인 넉오프+ 방법의 임계값이 FDR을 $q$이하로 통제하는지 알아보자.

넉오프+에서의 임계값 $T$에 대해서는 다음의 관계식이 성립한다.

\[\begin{align*} \text{FDP}(T) &= \frac{\#\{\text{null }j: W_j \geq T\}}{\max(\#\{j: W_j \geq T \},1)} \\ &= \frac{1+\#\{\text{null }j: W_j \leq -T\}}{\max(\#\{j: W_j \geq T \},1)} \cdot \frac{\#\{\text{null }j: W_j \geq T\}}{1+\#\{\text{null }j: W_j \leq -T\}} \\ &\leq \frac{1+\#\{j: W_j \leq -T\}}{\max(\#\{j: W_j \geq T \},1)} \cdot \frac{V^+(T)}{1+V^-(T)} \\ &= q \cdot \frac{V^+(T)}{1+V^-(T)} \text{ where } V^{\pm}(t) = \#\{\text{null }j: |W_j| \geq t, sgn(W_j) = \pm 1 \} \end{align*}\]

마팅게일 과정의 관점에서 $V^+(T)/(1+V^{-}(T))$가 슈퍼 마팅게일이고 이에 대한 정지시간을 $T$로 볼 수 있다면, 다음의 관계식이 성립할 수 있다.

\[\mathbb{E}[\frac{V^+(T)}{1+V^-(T)} ]\leq \mathbb{E}[\frac{V^+(0)}{1+V^-(0)}] = \mathbb{E}[\frac{V^+(0)}{1+p_0-V^+(0)} ]\leq 1\]

마지막 부등호는 이항분포 $Y \sim Bin(N,c)$에 대해 다음이 성립함을 이용한 것이다.

\[\begin{align*} \mathbb{E}[\frac{Y}{1+N-Y}] &= \sum_{y=1}^N\frac{y}{1+N-y}\cdot\frac{N!}{y!(N-y!)}\cdot c^y(1-c)^{N-y}\\ &= \sum_{y=1}^N \frac{N!}{(y-1)!(N-y+1)!}\cdot c^{y-1}(1-c)^{N-y+1} \cdot c(1-c)^{-1} \\ &= \sum_{y=1}^{N-1}Pr(Y=y) \cdot \frac{c}{1-c} \leq \frac{c}{1-c} \end{align*}\]

여기서 $Y=V^+(0),N=p_0,c=1/2$를 대입한 결과이다.

이제 $V^+(T)/(1+V^{-}(T))$가 슈퍼 마팅게일임을 보이자. 이를 위해 다음과 같이 표현을 다시 쓸 수 있다.

한편, $W_j=0$인 변수들은 선택되지 않으므로, 실제 검정에서 필요한 \(m=\#\{j:W_j\neq 0\}\)개의 변수들을 \(\mid W_{(1)}\mid \geq ... \geq \mid W_{(m)}\mid >0\)로 순서를 매겨서 이들을 임계점으로 고려해도 충분하다.

만약 $t=W_{(k)}(k=1,…,m)$라면 \(\#\{\ j\in[m]:\mid W_j \mid \geq t\} =k\)임으로 ${j\in[m]:1\leq j \leq k}$으로 대신하여 쓸 수 있다. 따라서, $V^{\pm}(t)$도 이산적인 과정 $V^{\pm}(k)(k=m,m-1,…,1,0)$으로 다시 쓸 수 있다. 표기상의 편의를 위해 $V^{\pm}(0)=0$이라고 하자.

Note. 시간은 $k=m,m-1,…,1,0$의 순서로 흐른다.

이제 $\mathcal{F}_k$를 모든 대립가설의 $W_j$값과 $k$시점 이후, 다시 말해서 모든 $k’(\geq k)$번째에서의 $V^{\pm} (k’)$ 정보를 포함하는 $\mathcal{F}_k$를 정의하자. 즉, \(\mathcal{F}_{k} \subset \mathcal{F}_{k-1}\)으로 포함관계가 작아지는 시그마필드이지만, $k=m,m-1,…,1,0$의 역방향으로 \(\mathcal{F}_m,\mathcal{F}_{m-1},...,\mathcal{F}_1,\mathcal{F}_0\)은 정보가 누적됨으로 backward filtration이다.

이제 $M(k) = V^+(k)/(1+V^{-}(k))$가 backward filtration에 따른 슈퍼마팅게일임을 보이자. $\mathcal{F}_k$에서 $V^{\pm}(k)$가 주어짐으로 $\mathcal{F}_k$-가측이기에 다음을 보이면 충분하다.

\[\mathbb{E}[M(k-1)|\mathcal{F}_k] \leq M(k), \ \forall k\]

$|W_{(k)}|$에 대응하는 가설의 인덱스를 $J(k)$라고 하자. 대립가설의 모든 정보를 알고 있으므로 $k$번째 시점에서 가설 $J(k)$가 대립가설인지 귀무가설인지의 여부는 판단할 수 있다.

$V^{\pm}(k)$ 는 귀무가설에 대한 정보임으로 $k$번째 시점에서 만약 가설 $J(k)$가 대립가설이라면, $M(k-1)=M(k)$로 변함이 없다. 따라서 위 부등식이 성립한다.

반대로 가설 $J(k)$가 귀무가설이라면, $W_{(k)}$의 부호는 독립으로 ${-1,1}$중 하나가 $1/2$의 확률로 결정되고, 이에 대응하는 $V^{\pm}(k)$에서 1이 줄어든다.

\[\begin{align*} M(k-1)&= \frac{V^+(k) - I[sgn(W_k)=1]}{1+V^-(k)-(1-I[sgn(W_k)=1])} \\ &= \frac{V^+(k) - I[sgn(W_k)=1]}{\max(V^-(k)+I[sgn(W_k)=1],1)} \end{align*}\]

귀무가설인 $W_k$의 부호는 $\mathcal{F}_k$에 포함되지 않는다. 하지만 위에서, 전체 $W_j$의 크기와, 대립가설들의 부호를 조건부로 고정하면 귀무가설들의 부호는 서로 독립으로 ${-1,1}$중 하나를 $1/2$의 확률로 갖음을 보였다.

또한 \(\mathcal{F}_k\)에서는 $|W_j| \geq |W_{(k)}|$를 만족하는 귀무가설에 대응하는 $W_j$의 부호가 $+1$은 $V^+(k)$개이고, $-1$은 $V^-(k)$개임을 알고 있다. 따라서 다음이 성립한다.

\[\begin{align*} \mathbb{E}[I[sgn(W_k)=1 \mid \mathcal{F}_k] &= Pr(sgn(W_k)=1\mid \mathcal{F}_k) \\ &= \frac{Pr(sgn(W_k)=1,\mathcal{F}_k)}{Pr(\mathcal{F}_k)} \\ &= \frac{\frac{1}{2} \cdot\binom {V^+(k)+V^-(k)-1}{V^+(k)-1}( \frac{1}{2})^{V^+(k)+V^-(k)-1}}{\binom {V^+(k)+V^-(k)}{V^+(k)}(\frac{1}{2})^{V^+(k)+V^-(k)}} \\ &= \frac{V^+(k)}{V^+(k) + V^-(k)}, \ k \in \mathcal{H}_0 \end{align*}\]

즉, $J(k)$가 귀무가설인 경우에 \(\mathbb{E}[M(k-1)\mid \mathcal{F}_k]\)는 다음과 같다.

\[\begin{align*} \mathbb{E}[M(k-1)|\mathcal{F}_k] &= \frac{V^+(k) - 1}{V^-(k)+1}\cdot Pr(sgn(W_k)=1) + \frac{V^+(k)}{\max(V^-(k),1)}\cdot Pr(sgn(W_k)=-1) \\ &=\frac{1}{V^+(k) + V^-(k)}\cdot [V^+(k)\cdot \frac{V^{+}(k)-1}{1+V^{-}(k)} + V^{-}(k)\cdot \frac{V^{+}(k)}{\max(V^{-}(k),1)}] \\ &= \begin{cases}M(k) &\text{if } V^-(k)>0 \\ V^{+}(k)-1=M(k)-1 &\text{if } V^-(k) =0 \end{cases} \end{align*}\]

따라서 모든 경우에 대해 $\mathbb{E}[M(k-1)|\mathcal{F}_k] \leq M(k)$을 만족하기에 $M(k)$는 슈퍼마팅게일이다.

이제 넉오프+의 임계값 $T$가 유효한 정지 시간임을 확인하자.

\[\begin{align*} T &= \min \{t \in \mathcal{W} : \frac{1+\#\{j: W_j \leq -t\}}{\max(\#\{j: W_j \geq t\},1)} \leq q\} \\ &= \max \{k \in [m] : \frac{1+\#\{1\leq j \leq k: W_j \leq -|W_{(k)}|\}}{\max(\#\{1\leq j \leq k: W_j \geq |W_{(k)}\},1)} \leq q\} \\ &= \max \{k \in [m] : \frac{1+N^-(k)}{\max(N^+(k),1)} \leq q\} \text{ where } N^{\pm}(k) = \#\{1\leq j \leq k: |W_j| \leq |W_{(k)}, sgn(W_j) = \pm 1 \} \\ &= \max \{k \in [m] : R(k) \leq q \} \text{ where } R(k) = \frac{1+N^-(k)}{\max(N^+(k),1)}=:K \end{align*}\]

여기서 \(A^{\pm}(k) = \#\{\text{non null } j: \mid W_j \mid \leq \mid W_{(k)} \mid , sgn(W_j)= \pm 1\}\)라고 정의하면, $N^\pm(k) = V^\pm(k)+ A^\pm(k)$를 만족하고, $A^\pm(k)$는 대립가설에 대한 정보임으로 $\mathcal{F}_k$에서 주어진다. 즉, $R(k)$는 $\mathcal{F}_k$-가측이다.

또한 정지시간이 $\hat{k}$라면, $k’\geq \hat{k}$에 대해서는 $R(k’) >q$여야 하고, 마찬가지로 $R(k’)(k’\geq k)$들은 $\mathcal{F}_k$-가측임으로 넉오프+의 임계값은 유효한 정지시간이다.

\[\{K=\hat{k}\} \Leftrightarrow \{R(\hat{k}) \leq q\} \cap \left(\cap_{l>\hat{k}}\{R(l) >q\} \right) \in \mathcal{F}_k\]

따라서 다음이 성립한다.

\[\begin{align*} \text{FDR} = \mathbb{E}[\text{FDP}(\hat{k})] \leq q \cdot \mathbb{E}[M(\hat{k})] \leq q\cdot \mathbb{E}[M(0)] \leq q \end{align*}\]