The risk inflation criterion

Foster, D. & George, E. (1994), ‘The risk inflation criterion for multiple regression’의 내용을 참고해서 글을 정리해보았다.

 

Basic set up

다음과 같은 선형 모델을 가정해보자.

\[\mathbf{y} = X_1\beta_1 + ... + X_p\beta_p + \epsilon = \mathbf{X} \beta + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0,\sigma^2I_n), \beta_1 \text{ is intercept term}, \mathbf{X} \text{ is fixed.}\]

여기서 estimator \(\hat{\beta}\)는 risk \(R(\beta, \hat{\beta})\)에 의해 평가될 것이다. 이번 포스팅에서는 다음과 같은 risk를 사용할 것이다.

\[R(\beta, \hat{\beta}) = \mathbb{E}_{\beta} |\mathbf{X}\hat{\beta} - \mathbf{X}\beta|^2\]

\(p>>N\)인 경우에 생각해볼 수 있는 방법은 subset selection 방법이다. 이번 포스팅에서는 subset section에 대해서만 다뤄볼 것이다. 이를 다음과 같이 나타내보자.

\[\begin{align*} \gamma &= (\gamma_1, ..., \gamma_p) \text{ where } \gamma_1=1, \gamma_i \in \{0,1 \} \text{ for } i=2,..,p \\ \hat{\beta}_{\gamma} &= ((\mathbf{X}D_{\gamma})^T\mathbf{X}D_{\gamma})^{-1}(\mathbf{X}D_{\gamma})^T\mathbf{y} \text{ where } D_{\gamma} = diag[\gamma] \end{align*}\]

in-sample에 대한 risk를 계산하기에, 좋은 모델을 찾는데 있어서 단순히 위의 $R$을 최소화하는 것은 적절해보이지 않고, 사실 least squares solution이 이에 대한 최적값이다. 따라서 다음 정의하는 risk 함수의 보정값인 risk inflation을 평가지표로 사용한다.

The risk inflation

해당 논문에서 사용하는 risk inflation을 정의하기 위해서는 oracle estimator를 먼저 정의해야한다. 이를 다음과 같이 표기해보자.

\[\begin{align*} \eta(\beta) &= (1,\eta_2,..., \eta_p) \text{ where } \eta_i = I[\beta_i \neq 0] \\ \hat{\beta}_{\eta} &= ((\mathbf{X}D_{\eta})^T\mathbf{X}D_{\eta})^{-1}(\mathbf{X}D_{\eta})^T\mathbf{y} \end{align*}\]

즉, \(\hat{\beta}_{\eta}\)는 correct predictors를 사용한 least squares estimator이다. (참고로, \(\eta(\beta)\)는 \(\beta\)를 모르기에 우리가 알 수 없는 값이다.)

이제 subset selection의 추정량인 \(\hat{\beta}_{\gamma}\)의 평가는 \(\gamma\)에 의해 정의되는 다음과 같은 risk inflation함수를 사용한다.

\[RI(\gamma) = \underset{\beta}{\text{sup}} \left\{ \frac{R(\beta,\hat{\beta}_{\gamma})}{R(\beta,\hat{\beta}_{\eta})} \right\}\]

즉, 작은 risk inflation을 갖는 \(\gamma\)는 oracle estimator \(\hat{\beta}_{\eta}\)에 대해 좋은 성능을 가지고 있는 것이다.

위에서 정의한 risk함수를 이용해 \(\hat{\beta}_{\eta}\)에 대한 risk를 구하면 다음과 같다.

\[R(\beta, \hat{\beta}_{\eta}) = \mathbb{E}_{\beta} |\mathbf{X}\hat{\beta}_{\eta} - \mathbf{X}\beta|^2 = tr \left[ Cov_{\beta}(\mathbf{X}\hat{\beta}_{\eta}) \right] = |\eta|\sigma^2 \\ \text{where } \eta \text{ is the number of nonzero components of } \eta\]

즉, risk inflation은 다시 다음과 같이 쓸 수 있다.

\[RI(\gamma) = \underset{\beta}{\text{sup}} R(\beta,\hat{\beta}_{\gamma}) / |\eta|\sigma^2\]

참고로 least squares estimator의 경우 risk는 \(p\sigma^2\)이므로, risk inflation은

\[RI(\gamma_{LS}) = \underset{\beta}{\text{sup}} \frac{p}{|\eta|} = \underset{\eta}{\text{max}} \frac{p}{|\eta|} = p\]

이다.

Note. 때때로 몇몇 coefficient가 0이 아니지만 매우 작은 경우에 더 좋은 성능을 낼 수 있다. 이러한 경우에 위의 risk inflation은 \(\hat{\beta}_{\eta}\)에 대한 risk의 보정은 적절하지 않을 수 있다. 이때는 다음과 같은 risk inflation 함수를 고려해 볼 수 있을 것이다.

\[\tilde{RI}(\gamma) = \underset{\beta}{\text{sup}} \frac{R(\beta, \hat{\beta}_{\gamma})}{\underset{\gamma}{\text{inf}} \ R(\beta, \hat{\beta}_{\gamma})}\]

나중에 살펴볼 예정이지만 \(RI\)와 \(\tilde{RI}\)는 둘 다 비슷한 결과를 갖는다.

case of $\sigma^2$ known

먼저 \(\sigma^2\)이 알려진 경우에 대해서만 다뤄볼 예정이다. \(\sigma^2\)이 알려지지 않은 경우에도 중요한 특징들은 여전히 알려진 경우와 같다.

지난 포스팅에서도 다뤘듯이 subset selection 문제는 다음과 같다.

\[\underset{\beta}{\text{min}} \left[SSE + \lambda\|\beta\|_0\right] \text{ where } \|\beta\|_0 = \sum_{j=1}^p I(\beta_j \neq 0)\]

이를 논문에서는 위에서 정의한 \(\gamma\)를 사용해서 다음과 같이 나타냈다.

\[\gamma_{\Pi} = \underset{\gamma}{\text{arg min}} \left[ SSE_{\gamma} + |\gamma|\sigma^2\Pi \right] \\ \text{ where } \Pi \geq 0 \text{ is a prespecified constant, } |\gamma| \text{ is the number of nonzero components of } \gamma\]

 

Note. \(\sigma^2\)이 알려진 경우의 AIC,\(C_p\),BIC는 모두 \(\gamma_{\Pi}\)의 특별한 케이스이다. 먼저 \(\sigma^2\)이 알려진 AIC는 다음과 같이 계산될 수 있다.

\[\gamma_{\text{AIC}} = \underset{\gamma}{\text{arg min}} \ \text{AIC} \text{ where AIC} = \frac{1}{2\sigma^2}\left[SSE_{\gamma} + |\gamma|\sigma^22 \right]\]

즉, \(\gamma_{\text{AIC}}\)는 \(\Pi=2\)인 \(\gamma_{\Pi}\)이다. 마찬가지로 \(C_p\)의 경우에는 다음과 같다.

\[\gamma_{C_p} = \underset{\gamma}{\text{arg min}}C_p \text{ where } C_p = [SSE_\gamma/\sigma^2] - (n-2|\gamma|)\]

\(C_p\)는 다시 다음과 같이 쓸 수 있다.

\[C_p = \sigma^{-2}[SSE_{\gamma} + |\gamma|\sigma^22] - n\]

이는 \(\gamma_{C_p}\)가 \(\gamma_{\text{AIC}}\)와 같다는 겻을 보여주고, 따라서 \(\Pi=2\)인 \(\gamma_{\Pi}\)이다.

마지막으로 BIC의 경우는 다음과 같다.

\[\gamma_{\text{BIC}} = \underset{\gamma}{\text{arg min}} \ \text{BIC} \text{ where BIC} = \frac{1}{2\sigma^2}\left[SSE_{\gamma} + |\gamma|\sigma^2(\log n) \right]\]

즉, \(\Pi=\log n\)인 \(\gamma_{\Pi}\)이다.

다음으로 계산상의 편의를 위해 \(\mathbf{X}\)의 모든 열벡터가 orthogonal이라고 가정해보자.

$\mathbf{X}^T\mathbf{X}$ is diagonal

즉, \(\mathbf{X}^T\mathbf{X}\)가 대각행렬일 경우 다음과 같이 \(\gamma_{\Pi}\)를 구할 수 있다.

\[\begin{align*} \gamma_{\Pi} &= \underset{\gamma}{\text{arg min}} |\mathbf{y} - \mathbf{X}\hat{\beta}_{\gamma} |^2 + |\gamma|\sigma^2\Pi \\ &= \underset{\gamma}{\text{arg min}} |\mathbf{X}\hat{\beta}_{\gamma_{LS}} - \mathbf{X}\hat{\beta}_{\gamma} |^2 + |\gamma|\sigma^2\Pi \\ &= \underset{\gamma}{\text{arg min}} \sum_{i=1}^p \left((\hat{\beta}_{\gamma_{LS}})_i - (\hat{\beta}_{\gamma})_i \right)^2X_{i}^TX_{i} + |\gamma|\sigma^2\Pi \\ &= \underset{\gamma}{\text{arg min}} \sum_{i=1}^p \left[I(\gamma_i=0)\frac{(X_i^T\mathbf{y})^2}{X_i^TX_i} + I(\gamma_i=1)\sigma^2\Pi \right] \\ &= \{1, \gamma_2^*...\gamma_p^*\} \text{ where } \gamma_i^* = I\left[ \frac{(X_i^T\mathbf{y})^2}{X_i^TX_i} > \sigma^2\Pi \right] \text{ for } i=2,..,p \end{align*}\]

Calculate the risk of \(\gamma_{\Pi}\)

이번에는 \(\gamma_{\Pi}\)를 유도해보자. 먼저, \(\hat{\beta}_{\gamma}\)의 risk를 다음과 같이 분해할 수 있다.

\[\begin{align*} R(\beta, \hat{\beta}_{\gamma}) &= \mathbb{E}_{\beta}|\mathbf{X}\hat{\beta}_{\gamma} - \mathbf{X}\beta |^2 \\ &= \mathbb{E}_{\beta}\sum_{i=1}^p\left[ I(\gamma_i=0)\beta_i^2X_i^TX_i + I(\gamma_i=1)(\frac{X_i^T\mathbf{y}}{X_i^TX_i} - \beta_i)^2X_i^TX_i \right] \\ &= \mathbb{E}_{\beta}\sum_{\gamma_i=0}(|X_i|\beta_i)^2 + \mathbb{E}_{\beta}\sum_{\gamma_i=1}(\frac{X_i^T(\mathbf{y}-X_i\beta_i)}{X_i^TX_i})^2X_i^TX_i \end{align*}\]

즉 위 식의 첫번째 항은 subset selection에서 선택된 변수들의 risk에 대한 bias 항, 두번째항은 variance항으로 해석해볼 수 있다. 또한 모든 컬럼벡터들이 orthogonal이므로 다음이 성립한다.

\[X_i^T\epsilon = X_i^T(\mathbf{y} - \sum_{j=1}^pX_j\beta_j) = X_i^T\mathbf{y} - X_i^TX_i\beta_i (\because X_i^TX_j = 0 \text{ for } i\neq j)\]

즉 \(R(\beta, \hat{\beta_{\gamma}})\)의 두번째 항을 다음과 같이 나타낼 수 있다.

\[\begin{align*} R(\beta, \hat{\beta_{\gamma}}) &= \mathbb{E}_{\beta}\sum_{\gamma_i=0}(|X_i|\beta_i)^2 + \mathbb{E}_{\beta}\sum_{\gamma_i=1}(\frac{X_i^T(\mathbf{y}-X_i\beta_i)}{X_i^TX_i})^2X_i^TX_i \\ \end{align*}\]

마찬가지로 \(\gamma_{\Pi}\)에서의 지시함수는 다음과 같이 나타낼 수 있다.

\[\begin{align*} \gamma_i^* &= I\left[ \frac{(X_i^T\mathbf{y})^2}{X_i^TX_i} > \sigma^2\Pi \right]\\ &= I\left[ \frac{(X_i^T\epsilon + X_i^TX_i\beta_i)^2}{X_i^TX_i} > \sigma^2\Pi \right] \\ &= I\left[ \left(\frac{(X_i^T\epsilon)}{|X_i|} + |X_i|\beta_i \right)^2 > \sigma^2\Pi \right] \end{align*}\]

이제 \(\hat{\beta}_{\gamma_{\Pi}}\)를 대입하고, 처음 basic set up에서 가정한 오차의 정규성 가정을 이용하면 다음과 같이 나타낼 수 있다.( \((X_i^T\epsilon)|X_i| = \sigma Z \text{ where } Z \sim \mathcal{N}(0,1)\) )

\[\begin{align*} (|X_i|\beta_i)^2P[\gamma_i^* = 0] &=(|X_i|\beta_i)^2P\left[\left(\sigma^2Z + |X_i|\beta_i\right)^2 \leq \sigma\Pi \right] \\ \mathbb{E}_{\beta}\frac{(X_i^T\epsilon)^2}{|X_i|^2}I(\gamma_i^*=1) &= \sigma^2\mathbb{E}\left[ Z^2I \left[ \left(\sigma^2Z + |X_i|\beta_i\right)^2 > \sigma^2\Pi \right] \right] \end{align*}\]

그러므로 \(\gamma_{\Pi}\)에 대한 risk는 다음과 같다.

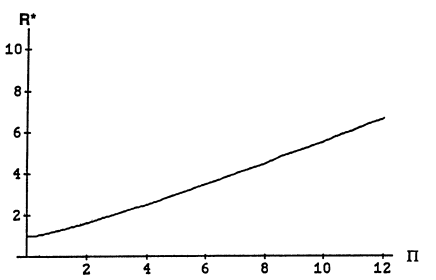
\[\begin{align*} R(\beta, \hat{\beta}_{\gamma_{\Pi}}) &= \sigma^2 +\sigma^2\sum_{i=2}^p R^*(\frac{|X_i|\beta_i}{\sigma}, \Pi) \\ & \text{ where} \\ R^*(w,\Pi) &= w^2P\left[(w+Z)^2 \leq \Pi \right] + \mathbb{E}\left[ Z^2I\left[ I(w+Z)^2 > \Pi \right] \right] \end{align*}\]

다음 그림은 위 risk에서 \(w, \Pi\)에 대한 함수 \(R^*\)의 그래프이다.

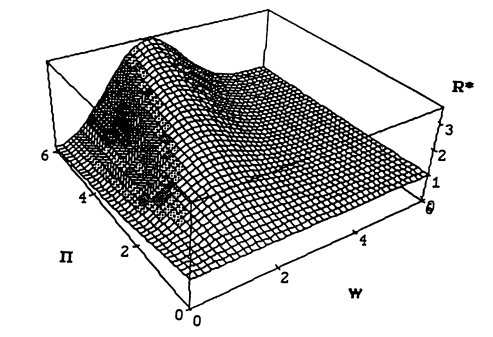
이번에는 \(\Pi\)를 고정시켜서 \(w = \frac{|X_i|\beta_i}{\sigma}\) 에 따른 \(R^*\)의 개형을 각각 보면 다음과 같다.

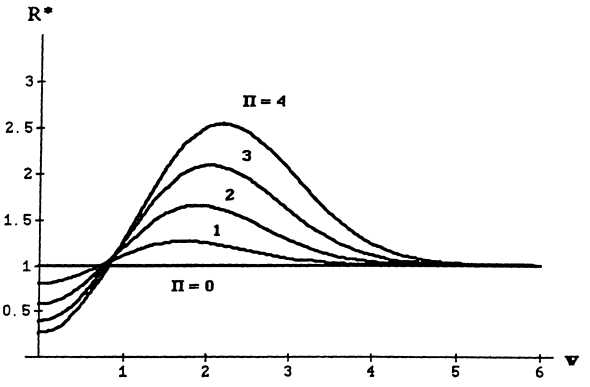
\(\Pi = 0\)인 경우에서 \(R^*\)가 모두 1인 이유는, 이때의 \(\gamma_{\Pi}\)는 \(\gamma_{\text{LS}}\) 즉, Overall Least squares estimator이기 때문이다. 또한 \(\Pi\)가 증가할수록 \(w\)에 따른 \(R^*\)의 변화량 폭이 커짐을 알 수 있다. (추가적으로 \(\Pi\)가 증가할때마다 \(R^*\)의 최댓값이 증가한다는 점을 유의하자.) 주목할만한 점은 \(R^*\)는 오직 오차에 대한 정규성 가정으로만 유도되었고, 이는 CLT에 의해 더 폭넓게 일반화할 수 있다.

Calculate the risk inflation of \(\gamma_{\Pi}\)

위에서 계산한 \(\gamma_{\Pi}\)에 대한 risk를 이용하기 위해 먼저 다음과 같은 partial risk inflation을 정의해보자.

\[RI(j, \gamma) = \underset{\beta \in B_j}{\text{sup}} \frac{R(\beta, \hat{\beta}_{\gamma})}{j\sigma^2} \text{ where } B_j = \{\beta : |\eta | = j \}\]

이는 즉, $j$개의 nonzero components를 갖는 $\beta$ 집합에 한해서만 최대의 risk를 구하는 것이다. 위 partial risk inflation에 \(R^*\)를 대입하면 다시 다음과 같이 나타낼 수 있다. (이 때 변수는 \(\beta\)임에 유의하자.)

\[\begin{align*} RI(j, \gamma_{\Pi}) &= \underset{\beta \in B_j}{\text{sup}}\frac{1}{j\sigma^2} \left[ \sigma^2 +\sigma^2\sum_{i=2}^p R^*(w_i, \Pi) \right] \\ &=\underset{\beta \in B_j}{\text{sup}}\frac{1}{j}\left[1 + \sum_{i=2}^p \left\{I(\beta_i=0)R^*(w_i=0,\Pi) + I(\beta_i \neq0)R^*(w_i,\Pi)\right\} \right] \\ &= \frac{1}{j}[1 + (p-j)R^*(0,\Pi) + (j-1)\underset{w}{\text{sup}}R^*(w,\Pi)] \end{align*}\]

즉 \(j\)와 \(\Pi\)에 대한 함수이며, $j$에 대해 monotone이다. 따라서 \(\gamma_{\Pi}\)에 대한 risk inflation은 다음과 같이 나타낼 수 있다.

\[\begin{align*} RI(\gamma_{\Pi}) &= \underset{j}{\text{max}}RI(j,\gamma_{\Pi}) = \max \left[ RI(1,\gamma_{\Pi}), RI(p,\gamma_{\Pi}) \right] \\ &= \max \left[ 1 + (p-1)R^*(0,\Pi), 1/p + (1-1/p)\underset{w}{\text{sup}}R^*(w,\Pi) \right] \\ &\approx \max \left[pR^*(0,\Pi), \underset{w}{\text{sup}}R^*(w,\Pi) \right] \text{ for large } p \end{align*}\]

따라서 \(\gamma_{\Pi}\)에 대한 risk inflation은 \(R^*(0,\Pi)\)와 \(\underset{w}{\text{sup}}R^*(w,\Pi)\)에 의해 결정됨을 알 수 있다. 다음은 \(\Pi\)에 따른 \(R^*(0,\Pi)\)와 \(\underset{w}{\text{sup}}R^*(w,\Pi)\)값을 구한 표이다. 아래 표를 통하여 AIC,$C_p$,BIC의 \(\Pi = 1,2,\log n\)과 충분히 큰 \(p\)에 대하여 \(Pi=0\)인 Least squares 경우의 risk inflation인 \(p\)보다 모두 작다는 것을 알 수 있다.

 

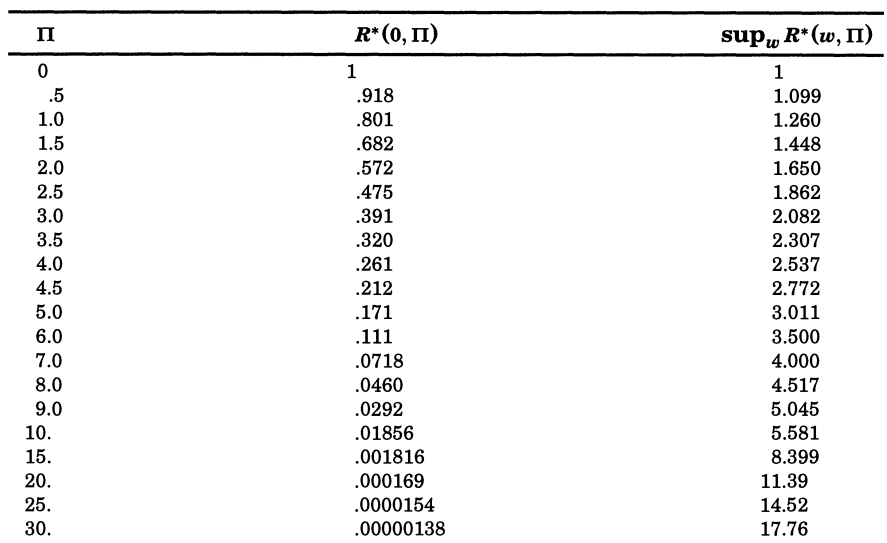
먼저, \(R^*(0,\Pi)\)는 \(\hat{\beta}_{\gamma_{\Pi}}\)에서 \(\beta_i=0\) 인 component에 대한 에러를 나타내는 양이다. 또한 이는 바로 다음과 같이 계산될 수 있다.

\[\begin{align*} R^*(0,\Pi) &= \mathbb{E} \left[ Z^2I(Z^2>\Pi) \right] = 2\left[\sqrt{\Pi}\phi(\sqrt{\Pi}) + \Phi(-\sqrt{\Pi}) \right] \\ &\approx 2\sqrt{\Pi}\phi(\sqrt{\Pi}) \text{ for large } \Pi \end{align*}\]

\(\phi, \Phi\)는 각각 표준정규분포의 pdf와 cdf이다. 따라서 \(R^*(0,\Pi)\)는 \(\Pi\)가 증가함에 따라 기하급수적으로 감소함을 알 수 있다.

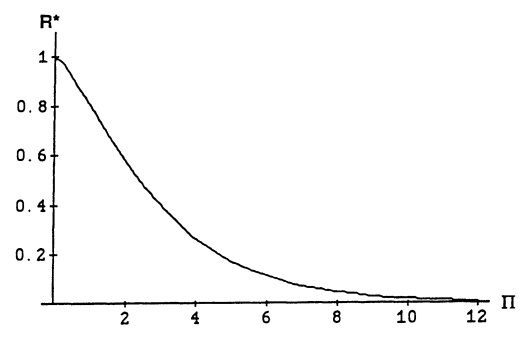
즉 \(\Pi\)가 증가할 수록 \(\beta_i=0\)인 항에 대한 예측이 더 정확해진다는 것을 알 수 있다. 여기서 trade-off 관계를 고려해보면 반대로 \(\underset{w}{\text{sup}}R^*(w,\Pi)\)은 \(\Pi\)가 증가함에 따라 마찬가지로 증가할 것임을 직관적으로 예상해볼 수 있을 것이다.

\(\underset{w}{\text{sup}}R^*(w,\Pi)\)의 경우, \(\gamma_{\Pi}\)에 대한 추정량에 대하여 가능한 최악의 조합에 대한 risk를 나타냄을 알 수 있다. \(\underset{w}{\text{sup}}R^*(w,\Pi)\)는 특정한 값으로 유도해낼 수 없지만 다음과 같은 근사가 가능하다.

\[\Pi - o(\Pi) < \underset{w}{\text{sup}}R^*(w,\Pi) < \Pi + 1 \ \text{ (see Lemma A.1 in the Appendix)}\]

즉, $\Pi$가 충분히 크면 \(\underset{w}{\text{sup}}R^*(w,\Pi)\)를 $\Pi$로 근사가 가능하다.

\(\underset{w}{\text{sup}}R^*(w,\Pi)\)에 대한 그래프는 다음과 같다. 이전 \(R^*\) 그래프에서도 보았듯이, \(\Pi\)가 증가함에 따라 선형적으로 증가함을 알 수 있다.

그러므로, 충분히 큰 \(p, \Pi\)에 대하여 \(\gamma_{\Pi}\)에 대한 risk inflation은 다음과 같이 근사될 수 있다.

\[RI(\gamma_{\Pi}) \approx \max \left[ p2\sqrt{\Pi}\phi(\sqrt{\Pi}), \Pi \right]\]

\(\Pi \approx 2\log p\) is optimal

이제 어떠한 \(\Pi\)를 선택해야 risk inflation을 가장 줄일 수 있을지 다뤄보자. 다음 그림은 \(p=2,10,10,200\)일 때의 partial risk inflation \(RI(1,\gamma_{\Pi}), RI(p,\gamma_{\Pi})\)을 나타낸 것이다. 이 때의 risk inflation은 두 함수에서의 최대값이다. 즉, risk inflation은 두 함수가 같아지는 지점에서 최솟값을 갖는다.

 

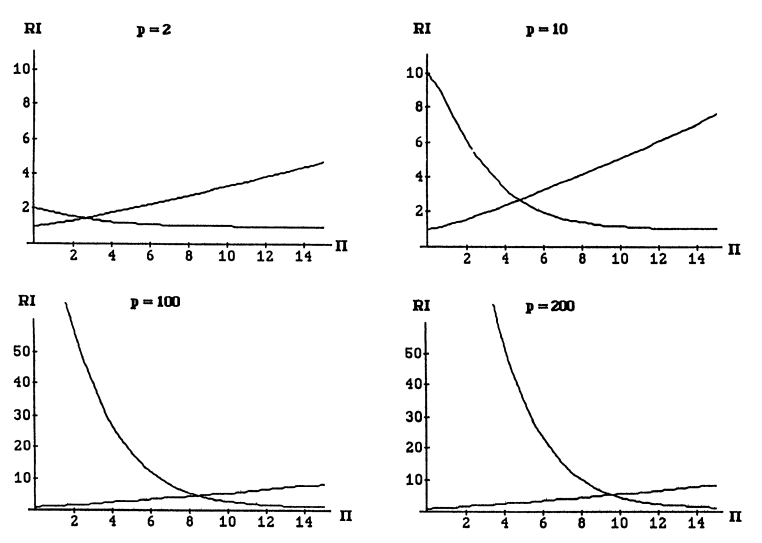
따라서 충분히 큰 \(p, \Pi\)에 대하여 근사하면 \(p2\sqrt{\Pi}\phi(\sqrt{\Pi}) = \Pi\)인 지점이 risk inflation이 최소인 \(\Pi\)이다. 해당 지점을 대략 나타내면 다음과 같다.

\[\Pi = 2\log p\]

또한 위 risk inflation 근사에서 \(RI(\gamma_{\Pi}) \approx \underset{w}{\text{sup}}R^*(w,\Pi) \approx \Pi\)임을 보였다. 즉 충분히 큰 $p$에 대하여 다음을 만족한다.

\[RI(\gamma_{2\log p}) \approx 2\log p\]

아래 표는 \(\Pi\)에 따른 risk inflation을 나타낸 것이다.

 

다음은 \(p \rightarrow \infty\)일 때, \(2\log p\)는 \(\gamma_{\Pi}\)뿐 아니라, 어떠한 \(\gamma\)에 대해서도 (즉 모든 변수 선택 방법에 대하여) 가능한 가장 작은 risk inflation을 가짐을 나타낸다.

\[\begin{align*} (1) \ RI(\gamma_{2\log p}) &< 1+2\log p \\ (2) \ \text{For any } \gamma, RI(\gamma) &\geq 2\log p - o(\log p) \end{align*}\]

먼저 \((1)\)에 대하여 증명해보자. 이는 \(j=1,p\)일 때의 partial risk inflation이 모두 \(1+2\log p\)보다 작음을 보이면 충분하다. 먼저 \(j=1\)인 경우는 다음과 같다. 이는 위에서 구한 \(R^*(0,\Pi)\)와 \(\underset{w}{\text{sup}}R^*(w,\Pi)\)의 구간을 이용하여 쉽게 유도할 수 있다.

(2)의 경우는 다음과 같다.

\[\begin{align*} RI(\gamma) &= \underset{j}{\text{max}} RI(j, \gamma) \\ &= \underset{j}{\text{max}} \frac{1}{j\sigma^2}\underset{\beta \in B_j}{\text{sup}}R(\beta, \hat{\beta}_{\gamma}) \\ &\geq \underset{j}{\text{max}} \frac{1}{j\sigma^2} \sigma^2\left[2(j-1)\log p - o(\log p) \right] \ \text{ (see Lemma A.2 in the Appendix)} \\ &\geq \underset{j}{\text{max}} \frac{j-1}{j}\left[ 2\log p - o(\log p)\right] \geq 2\log p - o(\log p) \end{align*}\]

(2)에 의하여 subset selection만이 아닌 모든 estimator \(\hat{\beta}\)에 대한 risk inflation에 대한 lower bound를 알 수 있다. 즉 \(p \rightarrow \infty\)일 때 lower bound는 \(2\log p\)이고, 이는 \(RI(\gamma_{2\log p})\)의 근사값과 같다. 추가적으로, \(\tilde{RI}\)의 경우, \(\Pi = 2\log p + 2\sqrt{2 \log p} + 1\)에 대하여 위의 (1)이 성립하여 따라서 \(\Pi \approx 2\log p\)인 지점에서 optimal이다.

For general \(\mathbf{X}^T\mathbf{X}\)

\(\mathbf{X}\)의 모든 컬럼이 orthogonal하지 않을 경우에도 \(\gamma_{\Pi}\)에 대한 risk inflation의 upper bound를 구할 수 있고, 적어도 변수 \(\mathbf{X}\)에 대한 가능한 가장 최악의 경우에 대해서는 \(\gamma_{\Pi}\)가 최선임을 알 수 있다. 다음의 증명과정들은 해당 논문의 Appendix에서 찾아볼 수 있다.

먼저, \(\xi = \sqrt{\Pi}\exp(\frac{1-\Pi}{2})\)를 정의해보자. 그렇다면 모든 \(\gamma_{\Pi}\)에 대하여 다음이 성립한다.

\[R(\beta, \hat{\beta}_{\gamma_{\Pi}}) \leq 2\sigma^2|\eta|(\Pi + 1) + \sigma^24\sqrt{2}(\frac{\Pi}{\Pi-1})^2e^{p\xi}\sqrt{p\xi}\]

이는 특히 \(p \rightarrow \infty\)이고, \(\Pi > 2\log p +2 \log \log p\)일 경우에 \(\eta=o(p^{-1})\)이므로 다음과 같다.

\[\begin{align*} R(\beta, \hat{\beta}_{\gamma_{\Pi}}) &\leq \sigma^22|\eta|(\Pi + 1) + o(1) \\ RI(\gamma_{\Pi}) &\leq 2(\Pi +1 ) + o(1) \end{align*}\]

위 식을 통해 가장 작은 upper bound는 \(\Pi \approx 2\log p\) 인 지점에서 구할 수 있고 diagonal인 경우의 2배인 \(4\log p\)임을 알 수 있다. 또한 임의의 \(\Pi\)에 대하여 다음이 성립한다.

\[\forall \Pi, \ \underset{\mathbf{X}}{\text{sup}} RI(\gamma_{\Pi}) \geq 4\log p - o(\log p)\]

따라서 \(\gamma_{2\log p}\)에서 \(4\log p\)의 upper bound를 갖기에 가장 optimal한 선택이라고 볼 수 있다. 물론 \(\mathbf{X}\)가 알려진 경우에는, 실제 계산을 통해 optimal한 \(\Pi\)를 구해볼 수 있을 것이다.

 

case of $\sigma^2$ unknown

\(\sigma^2\)이 알려지지 않은 경우에는 AIC,\(C_p\),BIC등을 포함한 많이 쓰는 변수 선택법들은 다음과 같다.

\[\gamma_{\hat{\Pi}} = \underset{\gamma}{\text{arg min}} \left[ SSE_{\gamma} + |\gamma|\hat{\Pi}\sigma^2 \right] \text{ where } \hat{\Pi} \geq 0 \text{ is a stochastic dimensionality penalty}\]

\(\gamma_{\Pi}\)에서 \(\Pi\)는 사전에 정의된 상수였지만, \(\hat{\Pi}\)은 데이터에 의존하는 확률변수임을 유의하자. 하지만 \(n \rightarrow \infty\)일 경우, \(\hat{\Pi}\)는 \(\Pi\)로 수렴한다. 예를 들어 \(C_p\)의 경우를 살펴보자. \(C_p\)에서는 다음과 같은 \(\sigma^2\) 추정량을 사용한다.

\[\hat{\sigma}^2_{LS} = \frac{1}{n-p}|\mathbf{y} - \mathbf{X}\hat{\beta}_{\gamma_{LS}}|^2\]

\(C_p\)는 다음과 같다.

\[\gamma_{C_p} = \underset{\gamma}{\text{arg min}}C_p \text{ where } C_p = \left[ SSE_{\gamma}\hat{\sigma}^2_{LS} \right] - (n-2|\gamma|)\]

이를 다시 쓰면 다음과 같다.

\[C_p = \hat{\sigma}^{-2}_{LS}\left[SSE_{\gamma} + |\gamma|\hat{\sigma}^2_{LS}2\right] - n\]

즉, \(\gamma_{C_p}\) 는\(\hat{\Pi} = \frac{2\hat{\sigma^2}_{LS}}{\sigma^2}\)일 때의 \(\gamma_{\hat{\Pi}}\)이다. 여기서 \(\Pi \rightarrow 2\), 즉 $n$이 충분히 클때 이는 \(\sigma^2\)이 알려져 있을 때의 \(\gamma_{C_p}\)와 같다.

일반적으로 많은 변수선택 방법은 \(\gamma_{\Pi}\) 꼴보다는 \(\gamma_{\hat{\Pi}}\)을 따른다. 한가지 예시로 adjusted \(R^2\)의 경우를 살펴보자.

\[\gamma_{aR^2} = \underset{\gamma}{\text{arg max}}\left[1 - \frac{SSE_{\gamma}/(n-|\gamma|)}{SST/(n-1)} \right] = \underset{\gamma}{\text{arg min}} SSE_{\gamma}/(n-|\gamma|)\]

이를 다시 쓰면 다음과 같다.

\[\frac{SSE_{\gamma}}{n-|\gamma|} = \frac{(n-|\gamma| )+ |\gamma|}{n(n-|\gamma|)}SSE_{\gamma} = \frac{1}{n}\left[SSE_{\gamma} + |\gamma|\frac{SSE_{\gamma}}{n-|\gamma|}\right]\]

따라서 adjusted \(R^2\)는 \(\hat{\Pi}=\frac{SSE_{\gamma_{aR^2}}}{n-|\gamma_{aR^2}|}\sigma^2\) 일 때의 \(\gamma_{\hat{\Pi}}\)이다. 여기서 충분히 큰 \(n\)에 대하여 \(\hat{\Pi} \rightarrow 1\)로 수렴하므로, adjusted \(R^2\)는 \(\Pi=1\)인 \(\gamma_{\Pi}\)와 대응한다. 이렇듯 대부분의 변수선택방법에서의 stochastic dimensionality penalty항 \(\hat{\Pi}\)는 \(n \rightarrow \infty\)일 때 수렴하고 비교적 stable하다.