[ESL 리뷰] 교재 7장-1 Model Assemssment and Selection

모델의 성능을 평가하는 것은 어떠한 모델과 파라미터를 선택할지를 나타내어주는 지표이며, 최종적으로 우리가 선택할 모델의 근거가 되므로 굉장히 중요한 과정이다. 이번 포스팅에서는 먼저 편향과 분산의 트레이드 오프 관계를 알아보고, 크게 in-sample error를 통해 prediction error를 추정하는 방법과 직접적으로 prediction error를 추정하는 방법론들을 알아볼 것이다.

Intro

일반적으로 데이터의 수가 충분히 많은 상황에서는 다음과 같이 train data, validation data, test data로 나누어, train data로 모델 학습을 진행한 후 validation data를 이용하여 가장 좋은 모델을 선정하는 model selection 단계, 마지막으로 test data를 이용하여 선택된 최종 모델의 prediction error를 추정하는 model assessment 단계가 있다.

하지만, 데이터의 수가 어느정도가 되면 충분히 많다고 할 수 있는지는 데이터셋 자체의 노이즈, 모델의 복잡성 등등을 고려하여 정확히 판단내릴 수 없기에 이번 포스팅에서는 분석적인 방법과 샘플 재사용을 통해 validation 단계를 추정하는 방법을 알아볼 것이다.

먼저 회귀 문제에 대해서 prediction error를 정의해보자. 데이터셋 \(\mathcal{T} = \left\{(x_i, y_i): i=1,...,N\right\}\)에 대하여 test error, expected test error, training error를 각각 다음과 같이 쓸 수 있다.

\[\begin{align*} &Err_{\mathcal{T}} = \mathbb{E} \left[L(Y, \hat{f}(X) | \mathcal{T} \right] &\text{(Test error or Generalization error)} \\ &Err = \mathbb{E}\left[ Err_{\mathcal{T}}\right]&\text{(Expected test error)} \\ &\bar{err} = \frac{1}{N} \sum_{i=1}^N L(y_i, \hat{f}(x_i)) &\text{(Training error)} \end{align*}\]

loss 함수로는 squared error, absolute error등을 쓸 수 있다. 실제 분석에서는 하나의 데이터셋만 주어지므로, test error보다는 expected test error를 추정하는 것이 더 적합하다. 분류 문제에 대해서는 다음과 같이 쓸 수 있다. 먼저, 반응 변수를 \(G \in \mathcal{G} = \left\{1,...,K\right\}\) 로 표현할 수 있고, \(p_k(X) = P(G=k|X)\) 를 각 클래스마다 추정하여, bayes classifier인 \(\hat{G}(X) = \underset{k}{\text{argmax }}\hat{p}_k(X)\)를 사용할 수 있다. loss 함수로는 0-1 loss나 deviance를 사용할 수 있다. deviance란 log likelihood에 -2를 곱한 값으로, -2를 곱한 이유는 가우시안 모델에서 squared error loss와 동치임을 맞춰주기 위함이다. 회귀모델에서와 같이 test error, expected test error를 다음과 같이 쓸 수 있다.

\[\begin{align*} &Err_{\mathcal{T}} = \mathbb{E} \left[L(G, \hat{G}(X) | \mathcal{T} \right] &\text{(Test error or Misclassification error)} \\ &Err = \mathbb{E}\left[ Err_{\mathcal{T}}\right] &\text{(Expected misclassification error)} \end{align*}\]

 

Bias, Variance and Model Complexity

먼저 에러의 기댓값이 0이고 등분산 \(\sigma_{\epsilon}^2\)를 갖는 \(Y = f(X) + \epsilon\)를 가정해보자. squaured error loss를 사용한다면 다음과 같이 \(x_0\)의 expected prediction error를 분해할 수 있다.

\[\begin{align*} Err(x_0) &= \mathbb{E}\left[ \left(Y- \hat{f}(x_0)\right)^2| X= x_0 \right] \\ &= \mathbb{E}\left[ \left(Y- f(x_0) + f(x_0) - \hat{f}(x_0)\right)^2| X= x_0 \right] \\ &= \mathbb{E}\left[ \left(Y- f(x_0) \right)^2 + \left(f(x_0) - \mathbb{E}\hat{f}(x_0) + \mathbb{E}\hat{f}(x_0) - \hat{f}(x_0)\right)^2| X= x_0 \right] \\ &= \sigma^2_{\epsilon} + \left\{ f(x_0) - \mathbb{E}\hat{f}(x_0) \right\}^2 + Var(\hat{f}(x_0)) \end{align*}\]

여기서 첫번째 항은 실제 값과 true model간의 차이로 발생하는 에러로 줄일 수 없는 오차이고, 두번째 항은 true model과 estimator의 차의 제곱, 즉 편향의 제곱이고, 마지막 항은 estimator의 분산이다. 첫번째 항은 우리가 조절할 수 없는 에러이므로, 일반적으로 편향과 분산 사이의 트레이드 오프 관계를 비교한다.

간단한 예시로, \(p\)차원 linear model \(\hat{f}_p(x) = x^T \hat{\beta}\)를 가정해보자. linear model의 편향은 다음과 같이 계산할 수 있다.

\[\begin{align*} \mathbb{E}\left[ f(x_0) - \mathbb{E}\hat{f}_{p}(x_0)\right]^2 &= \mathbb{E}\left[f(x_0) - x_0^T\beta\right]^2 + \mathbb{E}\left[x_0^T\beta - \mathbb{E}x_0^T\hat{\beta}\right] \\ &= \text{Ave}\left[\text{Model Bias}\right]^2 + \text{Ave}\left[\text{Estimation Bias}\right]^2 \end{align*}\]

첫번째 항은 true model과 선형 모델과의 차이로, 선형성을 가정하였을 때 생긴 편향이고, 두번째 항은 선형 모델과 우리의 추정량의 기댓값 사이의 차이로 발생하는 편향이다. 단순 linear model에서는 \(\hat{\beta}\)의 기댓값은 \(\beta\)이므로, 두번째 항은 0과 같다. 다음으로 분산을 계산해보자. 먼저 \(\mathbf{X}\)를 특잇값 분해를 통해 \(\mathbf{X} = \mathbf{U}\mathbf{D}\mathbf{V}^T, \ \mathbf{D} = \text{diag}(d_1,...,d_N)\)로 나타낼 수 있다. 이를 이용하여 분산을 다음과 같이 쓸 수 있다.

\[\begin{align*} Var\left[ x_0^T\hat{\beta}\right] &= x_0^TVar\left[(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \right]x_0 \\ &= \sigma_{\epsilon}^2x_0^T(\mathbf{X}^T\mathbf{X})^{-1}x_0 = \sigma^2_{\epsilon} \sum_{i=1}^N\frac{1}{d_i^2}z_i^2 \text{ where } \mathbf{z} = (z_1, ..., z_N) = V^Tx_0 \end{align*}\]

이번에는 ridge regression \(\hat{f}_{\alpha}\)를 고려해보자. \(\hat{\beta}_{\alpha}\)는 closed-form으로 \(\mathbf{X}(\mathbf{X}^T\mathbf{X}^T + \alpha \mathbf{I})^T\mathbf{X}^T\mathbf{y}\) (\(\alpha > 0\))로 나타낼 수 있다. linear model과 비교하였을 때, 편향의 경우 \(\hat{\beta}_{\alpha}\)의 기댓값이 \(\beta\)가 아니며 마찬가지로 선형 모델이기에 model bias는 같다.즉, 편향이 증가하였다. 반대로, 분산의 경우 다음과 같이 쓸 수 있다.

\[\begin{align*} Var\left[ x_0^T\hat{\beta}_{\alpha}\right] &= x_0^TVar\left[(\mathbf{X}^T\mathbf{X}+ \alpha \mathbf{I})^{-1}\mathbf{X}^T\mathbf{y} \right]x_0 \\ &= \sigma_{\epsilon}^2x_0^T VD^{*^{-1}}D^2D^{*^{-1}}V^Tx_0 \ \text{ where } D^* = \text{diag}(d_1^2 + \alpha, ... , d_N^2 + \alpha) \\ &= \sigma^2_{\epsilon} \sum_{i=1}^N\frac{d_i^2}{\left(d_i^2+\alpha\right)^2}z_i^2 \leq \sigma^2_{\epsilon} \sum_{i=1}^N\frac{1}{d_i^2}z_i^2 = Var\left[ x_0^T\hat{\beta}\right] \end{align*}\]

따라서 분산이 줄어들었음을 확인할 수 있다. 모델에 제약조건을 걸어 편향을 희생시키면서 분산을 줄임을 수식으로 파악해보았다. 이를 그림으로 나타내면 다음과 같다.

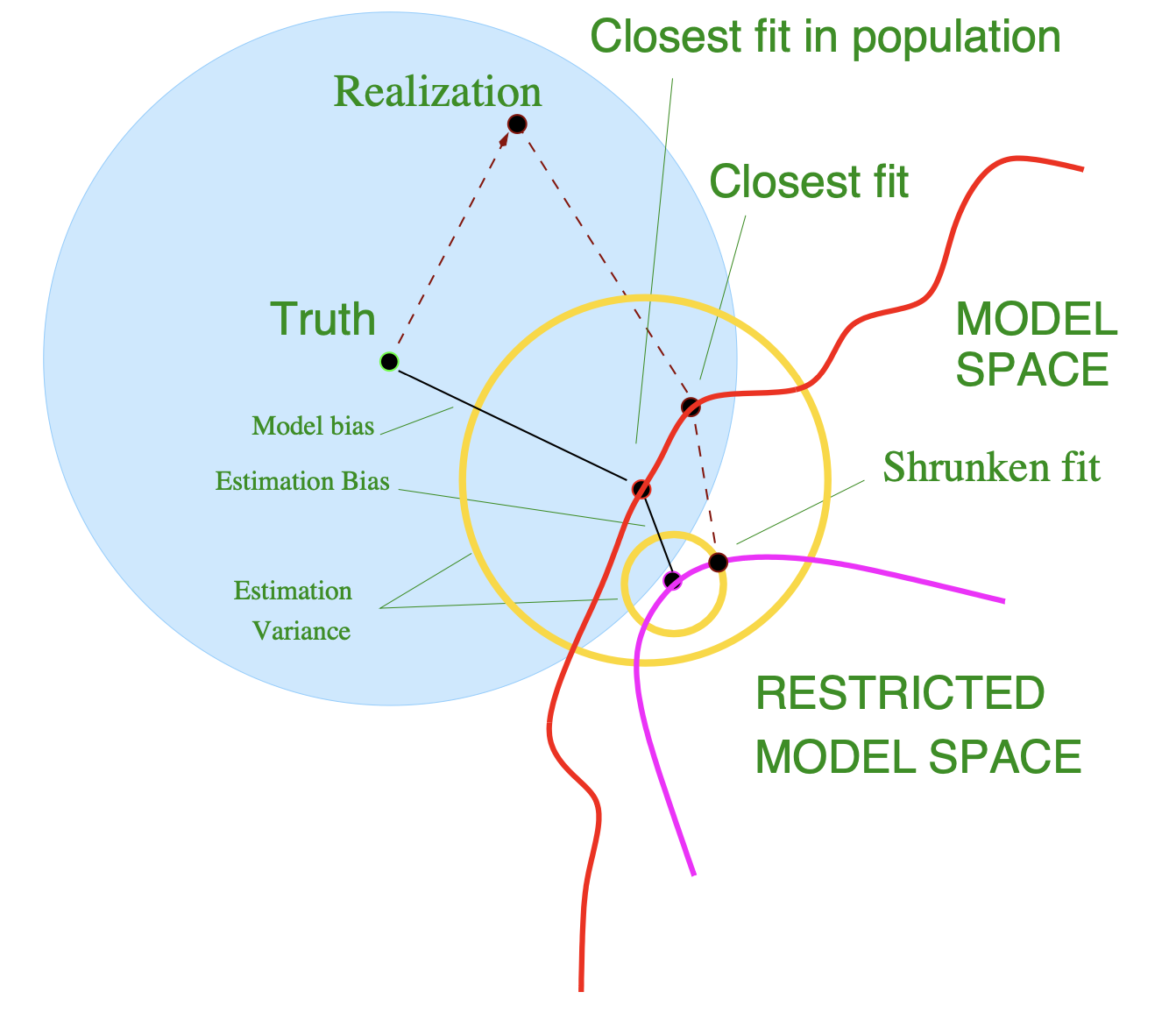
하지만, 분류 문제의 경우 expected prediction error는 편향과 분산간의 가법적인 관계가 아니기에, 완전한 trade off관계를 갖지는 않는다. 간단한 예시로 종속변수가 0과 1을 갖는 이진 분류문제를 가정해보자. \(Err_B(x_0) = P\left(G \neq G(x_0)\right)\)은 \(x_0\)에서 줄일 수 없는 베이즈 에러라고 볼 수 있다. \(f(x_0) = P\left(G=1|X=x_0\right)\) 이라고 하면, 다음이 성립한다.

\[Err(x_0) = Err_B{x_0} + | 2f(x_0) -1 | P\left( G(x_0) \neq \hat{G}(x_0) | X = x_0\right)\]

증명에 관해서는 \(G(x_0) = 1\)인 경우만 살펴보며 다음과 같다.

\[\begin{align*} Err(x_0) &= (1-f(x_0))\left(1-P(G\neq \hat{G}(x_0)|X=x_0)\right) + f(x_0)P(G\neq\hat{G}(x_0)|X=x_0) \\ &= 1-f(x_0) + (2f(x_0)-1)P(G\neq\hat{G}(x_0)|X=x_0) \\ &= P\left(G\neq G(x_0)\right) + (2f(x_0)-1)P(G\neq \hat{G}(x_0)|X=x_0) \end{align*}\]

이제 \(\hat{f}(x_0) \sim \mathcal{N}\left(\mathbb{E}\hat{f}(x_0), Var(\hat{f}(x_0)\right)\)라고 가정하면, \(x_0\)에서의 expected prediction error는 다음과 같다.

\[Err(x_0) = P\left(G \neq \hat{G}(x_0) | X = x_0 \right) \approx \Phi \left( \frac{\text{sign}\left(0.5 - f(x_0)\right)\left( \mathbb{E}\hat{f}(x_0) - 0.5 \right)}{\sqrt{Var(\hat{f}(x_0)}} \right)\]

\(f(x_0) > 0.5\)인 경우만 살펴보자. 즉, \(\text{sign}(0.5 - f(x_0)) = -1\)이므로 다음이 성립한다.

\[\begin{align*} P(Y \neq \hat{G}(x_0) | X = x_0) &= P(\hat{f}(x_0) < 0.5 | X = x_0) \\ &= P(\frac{\hat{f}(x_0) - \mathbb{E}\hat{f(x_0)}}{\sqrt{Var(\hat{f(x_0)})}} < \frac{0.5 - \mathbb{E}\hat{f(x_0)}}{\sqrt{Var(\hat{f(x_0)})}}) \\ &\approx \Phi \left( \frac{\text{sign}\left(0.5 - f(x_0)\right)\left( \mathbb{E}\hat{f}(x_0) - 0.5 \right)}{\sqrt{Var(\hat{f}(x_0)}} \right) \end{align*}\]

\(\text{sign}\left(0.5 - f(x_0)\right)\left( \mathbb{E}\hat{f}(x_0) - 0.5 \right)\)을 boundary-bias 항이라고 볼 수 있을 것이다. 즉, 편향과 분산의 관계가 가승적임을 알 수 있다. 이를 쉽게 이해할 수 있는 한가지 예시로, 만약 실제 확률이 0.8이지만 0.6으로 예측하여도, 둘 모두 1을 레이블로 삼으므로 prediction error는 0이다. 하지만 편향의 제곱은 0.04이고, 분산은 음이 아니므로 가법적이지 않음은 알 수 있다. 또한, \(\mathbb{E}\hat{f}(x_0)\)와 \(f(x_0)\)가 같은 레이블 상의 영역에 있을 때, 위 항은 음수이므로, 분산을 줄이는 것이 prediction error는를 줄일 수 있다. 하지만 반대로, 다른 영역에 있을 때는 오히려 분산을 늘리는 것이 에러를 줄일 수 있다는 것을 알 수 있다. 실제 편향은 \(f(x_0) - \mathbb{E}\hat{f}(x_0)\)이므로, 이 값이 작으면 boundary bias항은 보통 음수일 것이다. 따라서 잘 맞는 모델에 대해서는 분산을 줄이는 것이 알맞다고 할 수 있다. 분류 문제의 경우, \(f\)를 직접적으로 추정량으로 삼는게 아닌, 이를 바탕으로 레이블을 맞추기에 편향-분산 트레이드오프 관계가 더욱 복잡하다.

Estimate the bias and variance

Dietterich, Thomas G., and Eun Bae Kong. Machine learning bias, statistical bias, and statistical variance of decision tree algorithms. Technical report, Department of Computer Science, Oregon State University, 1995.의 내용을 참고하였다.

먼저 회귀문제의 경우를 살펴보자. 반복적으로 사이즈가 \(N\)인 데이터셋 \(\mathcal{T}_1, ...,\mathcal{T}_l\)을 생성해낼 수 있다고 가정해보자. 이는 부트스트랩을 이용하여 추출해낼 수 있다. 이를 이용하여 \(\bar{\hat{f}}(x_0) = \underset{l \rightarrow \infty}{\lim} \frac{1}{l} \sum_{i=1}^l \hat{f}_{\mathcal{T}_i}(x_0)\)를 계산하여, \(\mathbb{E}\hat{f}(x_0)\)를 추정해볼 수 있을 것이다. 마찬가지로 편향과 분산을 계산할 수 있다. 분류문제의 경우에는 직접적으로 종속변수를 추정한게 아닌, 레이블마다의 확률을 추정하여 bayes classifier를 이용하였기에 문제가 생긴다.

0-1 loss의 경우로 예를 들어보자. 먼저 misclassification error \(Err(x_0) = \mathbb{E} \left[ I\left(G \neq \hat{G}(x_0) \right) | X=x_0 \right]\) 는 \(\bar{\hat{p}} = \underset{l \rightarrow \infty}{\lim} \frac{1}{l} \sum_{i=1}^l I \left[ G \neq \hat{G}_{\mathcal{T}_i}(x_0)\right]\)로 추정을 해볼 수 있을 것이다. \(\mathbb{E}\hat{G}(x_0)\)의 경우, 단순히 평균을 취한다면 레이블에 해당하지 않는 값이 나오기에 문제가 생긴다. 따라서 여러번의 반복 중에 가장 많은 값이 나온 레이블, 즉 최빈값을 취해주는게 합리적일 것이다. \(\bar{\hat{G}}(x_0) = \text{Mode}\left( \hat{G}_{\mathcal{T}_1}(x_0), ... , \hat{G}_{\mathcal{T}_l}(x_0) \right)\)을 추정량으로 삼는다. 편향의 경우, \(\bar{\hat{p}} > 0.5\)일 때 \(x_0\)에서 평균적으로 분류를 잘하지 못한다고 볼 수 있다. 따라서 편향을 다음과 같이 정의한다.

\[I \left( \bar{\hat{p}} > 0.5 \right) = I\left(G \neq \mathbb{E}\hat{G}(x_0)\right)\]

분산의 경우, 위에서 확인했듯이 분류에서의 편향-분산 트레이드 오프 관계는 가법적이 아니지만 이에 비유하여 다음과 같이 정의하자.

\[(\text{Variance}) = \begin{cases} \bar{\hat{p}} \ \text{ if } \bar{\hat{p}} \leq 0.5 \\ 1 - \bar{\hat{p}} \ \text{ if } \bar{\hat{p}} > 0.5 \end{cases}\]

이는 다시, \(P\left(\hat{G}(x_0) \neq \mathbb{E}\hat{G}(x_0)\right)\)로 쓸 수 있고, \(\underset{l \rightarrow \infty}{\lim} \frac{1}{l} \sum_{i=1}^l I\left( \hat{G}_{\mathcal{T}_i} \neq \bar{\hat{G}}(x_0)\right)\)를 추정량으로 삼을 수 있다. 왜 이렇게 쓸 수 있는지는 다음과 같다.

먼저 편향이 0일 경우, 편향-분산의 트레이드 오프 관계를 이용하여 다음과 같이 쓸 수 있다.

\[Err(x_0) = P\left(G \neq \hat{G}(x_0)\right) = 0 +(\text{Variance}) = P\left(\hat{G}(x_0) \neq \mathbb{E}\hat{G}(x_0)\right)\]

편향이 1인 경우는 다음과 같다.

\[Err(x_0) = P\left(G \neq \hat{G}(x_0)\right) = 1 - P\left( Y = \hat{G}(x_0)\right)\]

편향이 1이라는 것은 \(G \neq \mathbb{E}\hat{G}(x_0)\)를 의미하므로, \(G = \hat{G}(x_0)\)일 경우, \(\hat{G}(x_0) \neq \mathbb{E}\hat{G}(x_0)\)이다. 즉 다음과 같이 쓸 수 있다.

\[Err(x_0) = 1 - P\left(\hat{G}(x_0) \neq \mathbb{E}\hat{G}(x_0)\right) = (\text{Bias}) - (\text{Variance})\]

이를 구현한 코드는 여기서 확인해볼 수 있다.

In-Sample Error and Extra-Sample Error

피팅된 모델은 학습데이터에 적응적이므로\(\bar{err}\)은 \(Err_{\mathcal{T}}\)에 대한 지나치게 낙관적인 추정량이다. 테스트 데이터는 학습 데이터와 겹칠 수도 있고, 아닐 수도 있기에 \(Err_{\mathcal{T}}\)를 extra sample error라고 생각해볼 수 있다. 먼저, optimism을 이해하기 위해 다음과 같이 in sample error를 정의하자.

\[Err_{in} = \frac{1}{N} \sum_{i=1}^N \mathbb{E}_{Y^0} \left[L(Y^0_i, \hat{f}(x_i) | \mathcal{T} \right]\]

\(Y_0\)은 각각의 학습데이터 \(x_i\)로부터 생성된 새로운 종속변수이다. 훈련 데이터셋은 조건부로 고정된 값임을 유의하자. In sample error와 \(\bar{err}\)의 차이를 optimism이라고 정의한다.

\[\begin{align*} &op = Err_{in} - \bar{err} \\ &w = \mathbb{E}_{\mathbf{y}}(op) \ (\because \mathcal{T} \text{ is fixed.} ) \end{align*}\]

마찬가지로 실제 학습데이터셋은 하나로 주어져 있으므로 \(Err_{\mathcal{T}}\) 대신 \(Err\)를 추정하는 것과 같이, \(w\)를 추정하는 것이 일반적이다. squared erro loss를 예로 들어 \(w\)를 다음과 같이 쓸 수 있다.

\[\begin{align*} w &= \frac{1}{N}\sum_{i=1}^N \mathbb{E}_{\mathbf{y}} \left[ \mathbb{E}_{Y^0} \left( Y^0_i - f(x_i) + f(x_i) - \mathbb{E}_{\mathbf{y}}\hat{Y}_i + \mathbb{E}_{\mathbf{y}}\hat{Y}_i - \hat{Y}_i \right)^2 - \left( Y_i - f(x_i) + f(x_i) - \mathbb{E}_{\mathbf{y}} \hat{Y}_i + \mathbb{E}_{\mathbf{y}} \hat{Y}_i - \hat{Y}_i \right)^2 \right] \\ &= \frac{1}{N}\sum_{i=1}^N \mathbb{E}_{\mathbf{y}} \left[ \mathbb{E}_{Y^0} \left( Y_i^0 - f(x_i) \right)^2 + 2 \mathbb{E}_{Y^0} \left( Y_i^0 - f(x_i) \right) \left( \hat{Y}_i - \mathbb{E}_{\mathbf{y}}\hat{Y}_i \right) - \left(Y_i - f(x_i) \right)^2 \right] \\ &= \frac{2}{N}\sum_{i=1}^N \mathbb{E}_{\mathbf{y}} \left[ \left( Y_i^0 - \mathbb{E}_{Y^0}Y^0_i \right) \left( \hat{Y}_i - \mathbb{E}_{\mathbf{y}}\hat{Y}_i \right)\right] = \frac{2}{N} \sum_{i=1}^N Cov(\hat{Y}_i ,Y_i) \end{align*}\]

즉, 추정량에 있어서 학습 데이터 \(Y_i\)의 영향이 클수록, optimism은 커짐을 알 수 있다. 또한 \(d\)개의 변수를 갖는 선형모델의 경우 \(\hat{\mathbf{y}} = \mathbf{H}\mathbf{y}\)이므로 (\(rank(\mathbf{H}) = tr(\mathbf{H}) = d\)), \(w = \frac{2}{N} tr\left[ Cov (\mathbf{H}\mathbf{y}, \mathbf{y})\right] = \frac{2d}{N}\sigma_{\epsilon}^2\)이다. 따라서 다음이 성립한다.

\[\mathbb{E}_{\mathbf{y}} Err_{in} = \mathbb{E}_{\mathbf{y}}\bar{err} + \frac{2d}{N}\sigma_{\epsilon}^2\]

위 관계식은 엔트로피를 사용하는 이진모델과 같은 다른 다양한 모델에서도 근사적으로 성립한다. prediction error를 추정하는 방법으로, optimism을 추정하여 위 관계식을 이용해 \(\bar{err}\)를 더한 값을 추정량으로 삼는 방법들로는 선형모델인 경우에 다음에 소개할 \(C_p\), AIC, BIC등이 있다. 이와 달리, 더 다양한 모델에 적용할 수 있도록 직접적으로 \(Err\)을 추정하는 방법으로 cross validation, bootstrap등이 있다. 실제 테스트 데이터가 학습데이터와 겹치지 않기에 in-sample error를 통한 추정량이 맞지 않을 것이라 생각할 수 있지만, 결국 우리가 prediction error를 추정하는 이유는 여러 모델들 중에 가장 좋은 모델을 찾는 것이므로, 절대적인 값을 찾는 것이 아닌, 모델간의 상대적인 차이만 알아내면 충분하다. 그렇기에 일반적으로 in-sample error를 통한 모델 선택은 효율적인 방법이라고 할 수 있다.

 

Estimating the in-sample error

일반화된 형태의 in-sample error 추정량은 다음과 같다.

\[\hat{Err_{in}} = \bar{err} + \hat{w}\]

선형 모델에서 \(d\)개의 파라미터를 갖는 squared error loss를 사용한 추정량은 다음과 같고, 이를 \(C_p\)통계량이라고 한다.

\[C_p = \bar{err} + \frac{2d}{N}\hat{\sigma}^2_{\epsilon}\]

해당 통계량을 이용하여 적절한 predictor의 개수 \(d\)를 선정할 수 있다. AIC의 경우 \(C_p\)의 일반화된 통계량으로 log-likelihood loss를 이용한다. AIC는 다음 근사식을 바탕으로 하는데, 이는 위의 \(\mathbb{E}_{\mathbf{y}} Err_{in}\)에 관한 관계식과 유사하다.

\[-2\mathbb{E}\left[ \log Pr_{\hat{\theta}}(Y)\right] \approx -\frac{2}{N}\mathbb{E}\left[\text{loglik}\right] + \frac{2d}{N}\]

\(Pr_{\theta}(Y)\)는 true density를 포함하는 \(Y\)의 density model들의 집합이고, \(\hat{\theta}\)는 \(\theta\)의 MLE 추정량이며, \(\text{loglik}\)은 \(\hat{\theta}\)를 대입한 log-likelihood 값이다. Gaussian model을 예로 살펴보자. 선택된 predictor들의 집합 \(\mathcal{M}\)에 대하여, log-likehood를 편미분하여 구한 MLE추정량은 \(\hat{\beta}_{\mathcal{M}}\)는 \(\mathbf{X}_{\mathcal{M}}\)의 LSE, \(\hat{\sigma}_{\mathcal{M}}^2\)는 \(\hat{\beta}_{\mathcal{M}}\)에 대한 \(\bar{err}_{\mathcal{M}}\)이다. 즉 모델 \({\mathcal{M}}\)에 대한 \(\text{loglik}(\mathcal{M})\)는 다음과 같다.

\[\begin{align*} \text{loglik}(\mathcal{M}) &= -N\log{\sqrt{2\pi\hat{\sigma}_{\mathcal{M}}^2}} - \frac{SSE_{\mathcal{M}}}{2\hat{\sigma}_{\mathcal{M}}^2} \\ &= -\frac{N}{2}\log2\pi - \frac{N}{2}\log\bar{err}_{\mathcal{M}} - \frac{N}{2} \end{align*}\]

따라서 AIC는 다음과 같다.

\[\begin{align*} AIC(\mathcal{M}) &= -\frac{2}{N}\text{loglik} + \frac{2|\mathcal{M}|}{N} \\ &= \log 2\pi + \log\bar{err}_{\mathcal{M}} + 1 + \frac{2|\mathcal{M}|}{N} \\ &= \log 2\pi + \log\left(1 + \frac{\bar{err}_{\mathcal{M}} - \bar{err}}{\bar{err}}\right) + \log\bar{err} + 1 + \frac{2|\mathcal{M}|}{N} \\ &\approx \log 2\pi +\frac{\bar{err}_{\mathcal{M}} - \bar{err}}{\bar{err}}+ \log\bar{err} + 1 + \frac{2|\mathcal{M}|}{N} \end{align*}\]

마지막 근사식은 \(x=0\) 근방에서 \(\log(1+x) \approx x\)를 이용한 것이다. \(\bar{err} = \hat{\sigma}^2_{\epsilon}\)이며, \(\mathcal{M}\)에 대한 상수항을 제거해주면 다음과 같다.

\[AIC(\mathcal{M}) = \frac{1}{\hat{\sigma}_{\epsilon}^2}\left[\bar{err}_{\mathcal{M}} + \frac{2|\mathcal{M}|}{N}\hat{\sigma}_{\epsilon}^2\right] = \frac{1}{\hat{\sigma}_{\epsilon}^2}C_p(\mathcal{M})\]

즉, \(C_p\)와 동치이므로, 위에서 말한 AIC가 \(C_p\)의 일반화된 형태임을 확인해 볼 수 있다.

BIC는 베이지안 접근으로, 모델 후보 \(\mathcal{M}_1 ,... , \mathcal{M}_M\)에 대하여 훈련데이터셋을 조건부로하여 MAP를 한 것으로, 라플라스 근사를 통해 유도된다. BIC의 일반적인 형태는 다음과 같다.

\[BIC = -2 \text{loglik} + (logN)\cdot d\]

Gaussian model을 예로 들면, 아래와 같이 쓸 수 있다. 즉 AIC(\(C_p\))에서 두번째항의 \(2\)를 \(logN\)으로 대체한 것과 같다. 따라서 AIC에 비해 더 단순한 모델을 선택하는 경향이 있다.

\[BIC(\mathcal{M}) = \frac{N}{\hat{\sigma}_{\epsilon}^2}\left[\bar{err}_{\mathcal{M}} + \frac{\log N \cdot|\mathcal{M}|}{N} \hat{\sigma}_{\epsilon}^2\right]\]

BIC의 경우 true model이 포함된 모델 후보들 중 \(N \rightarrow \infty\)이면 true model을 선택하지만, AIC의 경우는 더 복잡한 모델을 선택하는 경향이 있다. 반대로 \(N\)이 작은 경우, BIC는 너무 단순한 모델을 선택하는 경향이 있다. 더 자세한 in-sample prediction들의 관계에 대해서는 risk inflation을 다룬 이전포스팅을 참고하자.

Vapnik-Chervonenkis Dimension

위에서 제시된 방법론들은 모두 파라미터의 개수 \(d\)를 특정해야 했다. 일반적인 선형모델의 경우 \(\hat{\mathbf{y}} = \mathbf{S}\mathbf{y}\)꼴로 나타낼 수 있고, \(tr(\mathbf{S})\)을 자유도로 삼았다. 하지만, 비선형모델의 경우에는 이를 특정할 수 없다는 문제가 발생한다. 또한 파리미터의 개수를 모델의 복잡도에 대한 패널티항으로 삼았는데, 파라미터의 개수가 많은 모델이 반드시 더 복잡한 모델이라고 할 수 없다. 예를 들어 \(\alpha\)를 파라미터로 삼는 모델들의 집합 \(\left\{ f(x, \alpha) \right\}\)을 가정해보자. \(f(x, \alpha) = I\left( \alpha_0 + \alpha_1^Tx\right)\)(\(x \in \mathbb{R}^2\))인 모델 후보 집합과, \(f(x, \alpha) = I \left(\sin \alpha x\right)\)(\(x \in \mathbb{R}\)) 집합을 비교해보자. 전자의 경우 파라미터의 개수가 2개이고, 후자는 1개이다. 하지만, 다음 그림과 같이 전자는 최대 3개의 샘플을, 후자는 적절하게 \(\alpha\)를 선정하면 무한히 많은 샘플을 구별할 수 있음을 알 수 있다.

 

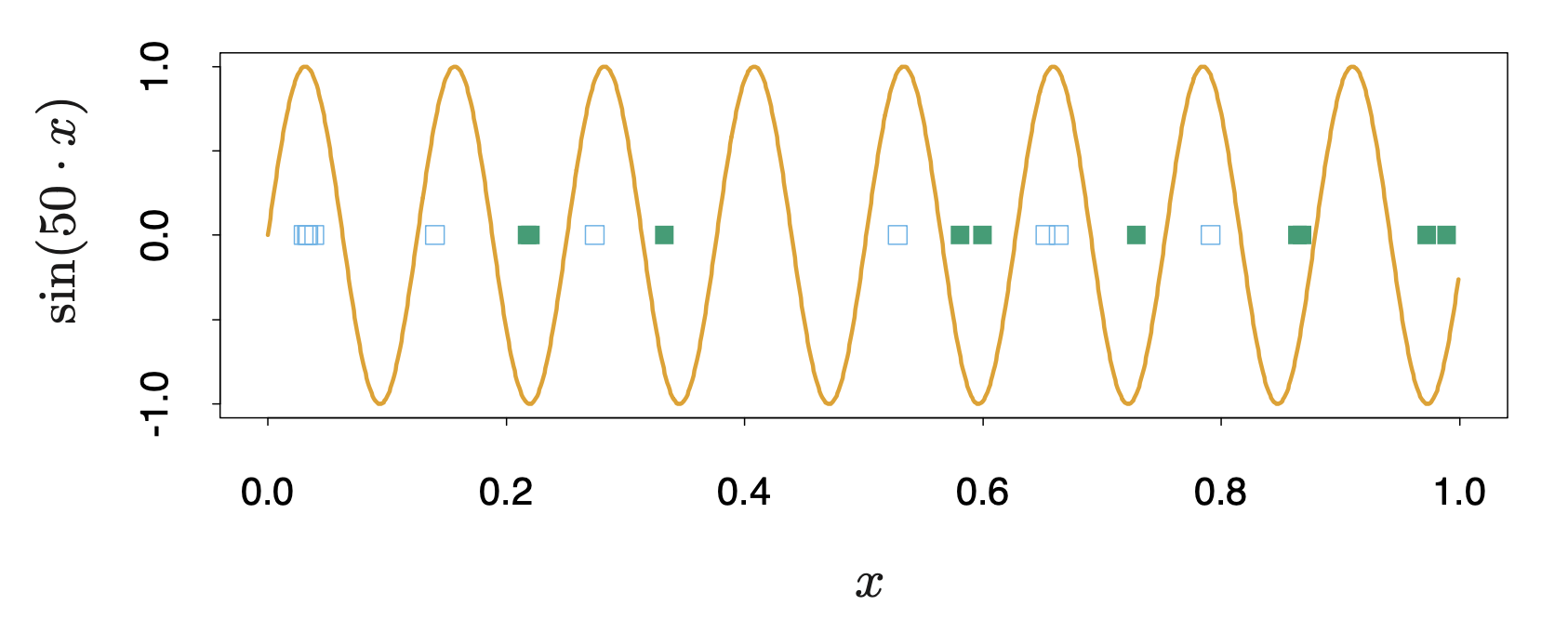
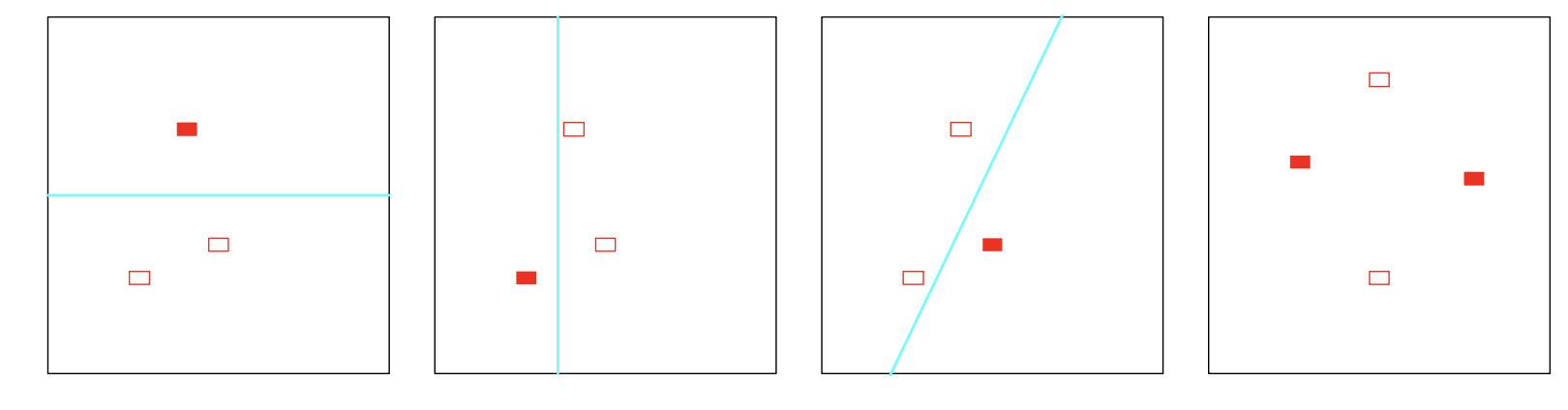
Vapnik-Chervonenkis Dimension(VC dimension)은 모델 집합의 복잡도를 측정할 수 있는 측도로, 모델 집합 \(\left\{ f(x, \alpha) \right\}\)가 나눌 수 있는 가장 많은 샘플 수 이다.예를 들어 \(\left\{ f(x, \alpha) \right\}\)가 단순 상수일 경우 나눌 수 있는 샘플이 없으므로, VC dimension은 0이다. 단순 특정 값을 threshold로 나누는 classifier의 경우, 특정 샘플을 기준으로 하나의 점을 나눌 수는 있지만, 일차원에서 0에 속하는 샘플보다 크거나 작은 두개의 샘플이 1에 속할 경우 나눌 수 없으므로, VC dimension은 1이다. 또한 위와 같은 \(\mathbb{R}^p\)상에서의 선형의 지시함수 집합은 VC dimension이 \(p+1\)이다.

VC dimension을 이용하여 \(N\)개의 샘플을 갖는 데이터셋에 대하여, VC dimension이 \(h\)인 모델 집합 \(\left\{ f(x, \alpha) \right\}\)에 대한 \(Err_{\mathcal{T}}\)에 대한 상한을 구할 수 있다.

\[\begin{align*} &P\left[Err_{\mathcal{T}} \leq \bar{err} + \frac{\epsilon}{2}\left( 1 + \sqrt{1+ \frac{4\bar{err}}{\epsilon}}\right) \right] \geq 1 - \eta \ &(\text{binary classification}) \\ &P\left[Err_{\mathcal{T}} \leq \frac{\bar{err}}{\left(1-c\sqrt{\epsilon}\right)_+} \right] \geq 1 - \eta \ &(\text{regression})\\ &\text{ where } \epsilon = a_1\frac{h\left[ \log(a_2N/h) + 1 \right] - \log(\eta/4)}{N}, \ 0< a_1 \leq4, 0<a_2\leq2 \end{align*}\]

일반적으로 \(c=1\)을 추천하고, 회귀의 경우 \(a_1 = a_2 = 1\), 분류의 경우 따로 추천은 없고, \(a_1 = 4, a_2=2\)인 경우가 최악의 경우에 대한 상한이다. 또한, 회귀문제의 경우 다음과 같은 practical bound가 있다.

\[Err_{\mathcal{T}} \leq \bar{err}\left(1- \sqrt{\rho - \rho\log\rho + \frac{\log N}{2N}}\right)^{-1}_+ \text{ where } \rho = \frac{h}{N}\]

Vapnik’s structural risk minimization(SRM)은 VC dimension이 점점 증가하는 nested sequence인 모델 집합을 피팅하면서 가장 작은 상한을 가지는 모델을 선택하는 방법이다. 예를 들어, 다항식 꼴의 \(\left\{ f(x, \alpha) \right\}\)를 잡아, 차수를 늘려나가면서 가장 좋은 모델을 선정할 수 있을 것이다.

Example

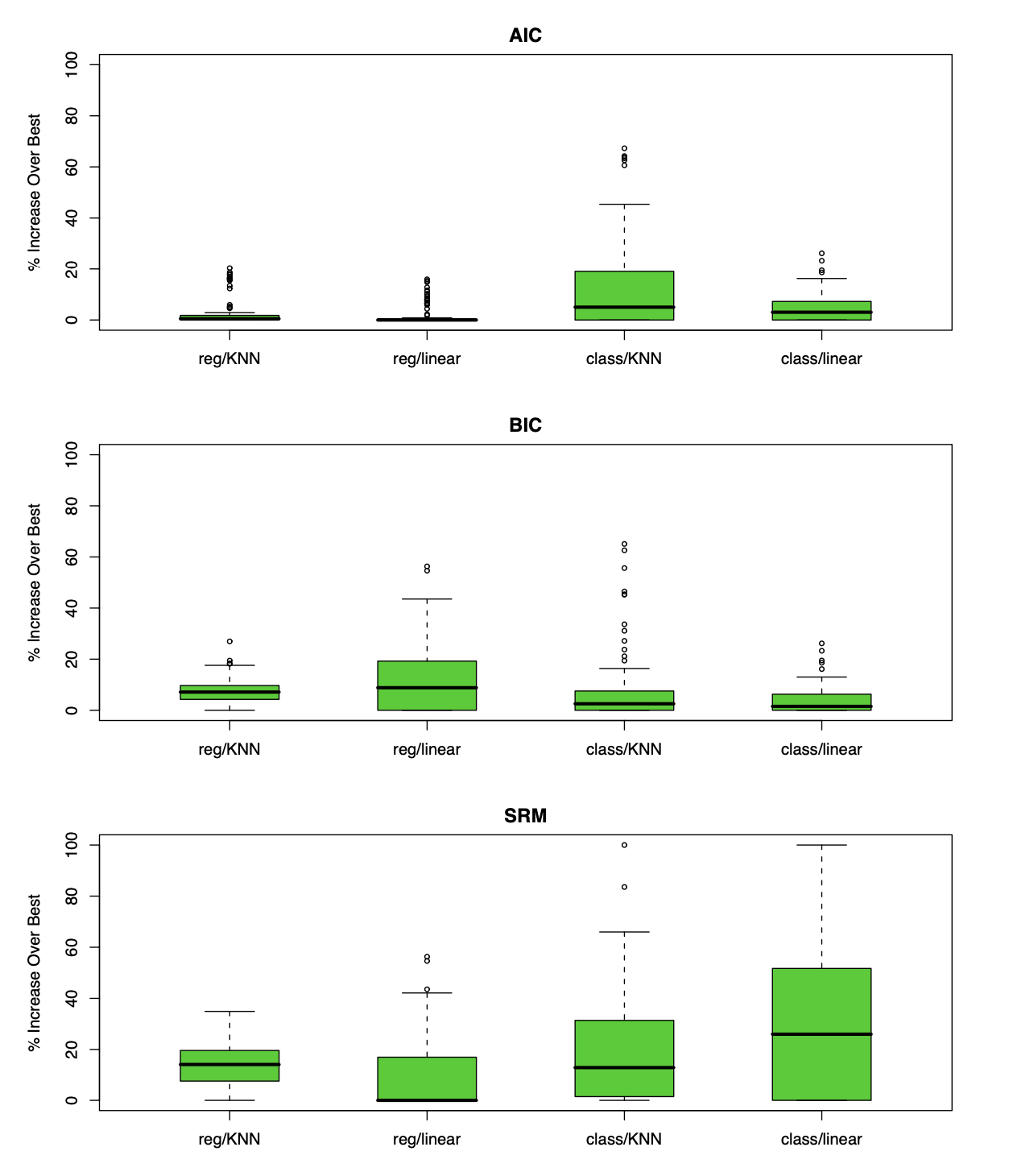
80개의 샘플 수를 갖는 \(p=20\)인 균등 분포 데이터셋 \(\mathbf{X}_1, ...,\mathbf{X}_{100}\)에 대해 k-NN의 경우, \(X_1\)이 0.5보다 작거나 같으면 \(0\)아니면 \(1\)이 되도록 라벨링을 하고, linear regression의 경우 \(\sum_{j=1}^{10} X_j\)가 \(5\)보다 크면 \(1\), 아니면 0이 되도록 각각의 \(\mathbf{y}_1,...,\mathbf{y}_{100}\)을 만들어, 각각 회귀,분류 모델을 피팅해 총 4개의 모델이 만들어진다. 회귀의 경우 squared error, 분류 0-1 loss를 사용한다. 네가지 케이스 모두, 파라미터 \(\alpha\) 즉, \(k = 1,...,50, p=1,...20\)에 대하여 AIC, BIC, SRM을 수행한다. 자유도는 k-NN의 경우 \(N/k\)이고, linear regression은 \(p\)이다. SRM의 경우 \(a_1=a_2=c=1\)로 설정하여 practical bound를 계산하여 진행하였다. 각각의 데이터셋마다 best model \(\hat{\alpha}\)를 찾고, 모든 \(\alpha\)에 대하여 \(Err_\mathcal{T}\)의 추정량을 계산하여 다음과 같이 상대적 에러를 계산한다.

\[100 \times \frac{Err_{\mathcal{T}}(\hat{\alpha}) - \min_{\alpha}Err_{\mathcal{T}}(\alpha)}{\max_{\alpha}Err_{\mathcal{T}}(\alpha) - \min_{\alpha}Err_{\mathcal{T}}(\alpha)}\]

결과는 다음과 같다. AIC의 경우 선형 모델에 대한 squared error를 기반으로 하지만 네가지 경우 모두에서 좋은 성능을 보임을 알 수 있다. BIC도 이와 비슷하게 좋은 성능을 보이지만, SRM의 경우 class/linear에서는 좋지 않은 성능을 보임을 확인해 볼 수 있다.

다음 포스팅에서는 Cross-validation, Bootstrap 방법들에 대해 알아볼 것이다.