[ESL 리뷰] 교재 6장 Kernel Smoothers

이번 포스팅에서는 저번과 마찬가지로 \(\mathbb{R}^p\)상에서의 회귀 모델 \(f(X)\)에 대한 유연성을 더해주는 방법으로 커널 함수를 이용하는 모델을 알아볼 것이다. 단순하게 각 입력 데이터 포인트 \(x_0\)마다 학습데이터 포인트들에 커널함수 \(K_{\lambda} (x_0, x_i)\)를 통한 가중치를 부여하여 모델을 피팅하는 방법이라 생각하면 된다. 이러한 방법은 memory-based 기법으로 모델 학습과정이 따로 없고, 단순 학습데이터들을 기억했다가, 예측하는 과정에서 모든 과정들이 일어난다는 특징이 있다. 해당 모델에서 우리가 결정해야할 파라미터는 커널 \(K_{\lambda}\)의 이웃의 너비를 결정하는 \(\lambda\)와 학습데이터가 있다. 이번 포스팅에서의 localization을 위한 커널은, 저번 포스팅에서의 RKHS에서 다룬 kernel methods와는 다른 함수라는 것을 유의하자. 즉, 이번 시간에 다룰 커널함수는 적분값이 1이며, 대칭이며 non-negative인 함수를 말한다.

One-Dimensional Kernel Smoothers

먼저 일차원 독립변수인 경우에 대해서 알아보자. Kernel smoothers을 이해하기 위해 먼저 k-NN에 대해 다시 서술해보자. k-NN은 다음과 같이 쓸 수 있고, 이는 회귀모델의 조건부 기댓값 \(\mathbb{E}(Y|X=x)\) 의 추정량이다.

\[\hat{f}(x) = Ave(y_i|x_i\in N_k(x))\]

즉, 입력데이터 \(x\)의 근방에 \(k\)개의 점들에 대한 \(y\)들의 평균값을 예측값으로 삼는다. 즉, \(x\)값이 변하면서 근방의 점들의 집합이 같을때 까지는 예측값이 일정하다가, 근방의 점들이 바뀔 때 바뀐 평균을 예측값으로 내놓기에 \(\hat{f}\)는 불연속적인 형태를 띌 수 밖에 없다. 하지만, 이러한 불연속성은 불필요하며, 보기 좋지 않다. 이를 해결하는 한 가지 방법으로, 가중치를 부여하여 \(x\)가 변하면서 예측값도 연속적으로 변할 수 있도록 하는 것이다. 다음은 이에 대한 한가지 예시인 Nadaraya-Watson 커널 가중 평균이다.

\[\hat{f}(x_0) = \frac{\sum_{i=1}^N K_{\lambda}(x_0, x_i)y_i}{\sum_{i=1}^N K_{\lambda}(x_0, x_i)}\]

커널함수로는 다음과 같은 함수들을 사용해볼 수 있다.

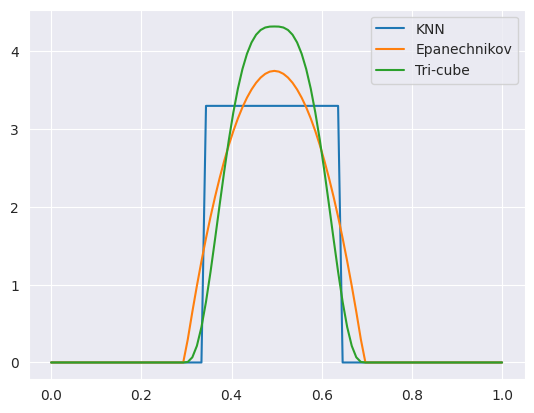
\[\begin{align*} &K_{\lambda}(x_0,x) = I\left[x \in (x_0-\lambda, x_0 + \lambda)\right]\frac{3}{4}\left[1-\left( \frac{x-x_0}{\lambda} \right)^2\right] &\text{ (Epanechnikov quadratic kernel)}& \\ &K_{\lambda}(x_0,x) = I\left[x \in (x_0-\lambda, x_0 + \lambda)\right]\left[1-\left| \frac{x-x_0}{\lambda} \right|^3\right]^3 &\text{ (Tri-cube kernel) }& \end{align*}\]

\(\lambda\)는 너비를 결정하는 smoothing parameter로 큰 값을 취할수록 너비가 커지기에 더 넓은 구간에서 가중평균을 취하기에 분산이 작아지고, 반대로 편향이 커지게되는 효과가 있다. \(x_0\)마다도 다른 너비를 부여하고 싶다면 더 일반적으로, \(h_{\lambda}(x_0)\)를 정의하여 사용해볼 수 있을 것이다.

위 표현법을 사용하여, k-NN의 커널은 다음과 같이 쓸 수 있다.

\[K_k(x_0,x) = I\left[x \in N_k(x)\right]\frac{1}{2|x_0 - x_{[k]}|} = I\left[x \in (x_0 - |x_0 - x_{[k]}|, x_0 + |x_0 - x_{[k]}|)\right]\frac{1}{2|x_0 - x_{[k]}|}\]

여기서 \(x_{[k]}\)는 \(x_0\)에서 \(k\)번째 가까운 훈련 데이터 포인트이다.

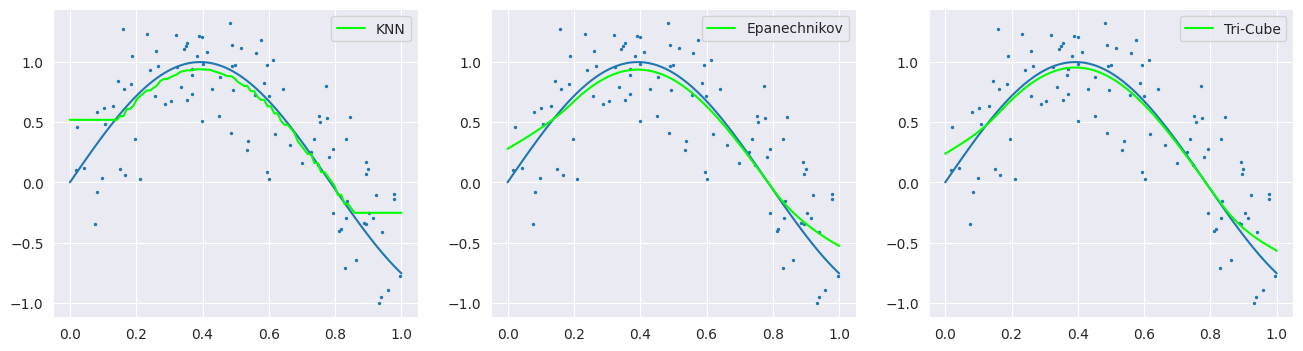
Nadaraya-Watson 커널 가중 평균의 단점은 훈련 데이터의 양 끝 경계의 경우 한 쪽 방향에서만 가중평균을 계산할 수 있기에 성능이 떨어진다는 단점이 있다. 다음은 \(Y_i = \text{sin}(4X) + \epsilon, \ X \sim U[0,1], \ \epsilon \sim \mathcal{N}(0,1/3)\)라 가정한 100개의 시뮬레이션 데이터에 대해 각각의 커널을 이용하여 NW 커널 가중 평균을 적용한 모델 피팅 결과이다. 파란 선을 위에서 가정한 true model이고 초록 선이 예측한 결과이다. 3개의 모델 모두 양 끝 경계에서 실제 값보다 크게 추정을 한다는 점을 알 수 있다. 실제로는 양 끝에서 감소하는 개형이지만, 왼쪽 경계에서는 증가하는 오른쪽에 대해서만, 반대로 오른쪽 경계에서는 감소하고 있지만 덜 감소한 왼쪽에 대해서만 평균을 취해주었기 때문이다. 이러한 문제를 boundary effect라고 한다.

Local Linear Regression

위에서 제시된 양 끝 경계에서 성능이 떨어지 이유는 커널에 대한 가중 평균을 취했지만, 실제 데이터는 각각의 경계에서 선형이기에, 이에 대한 편차 때문이다. 가중평균이라는 것은 결국 \(x_0\) 에 대해서는 상수이기에 \(x_0\)에 대한 선형인 모델을 이용하여 문제를 해결할 수 있다.

따라서 위와 같은 시뮬레이션 데이터에 대해서는 다음과 같이 가중선형 모델을 가정해보자.

\[\begin{align*} &\hat{f}(x_0) = \hat{\alpha}(x_0) + \hat{\beta}(x_0)x_0 \text{ where } \\ & \hat{\alpha}(x_0), \hat{\beta}(x_0) = \underset{\alpha(x_0) \beta(x_0)}{min} \sum_{i=1}^N K_{\lambda}(x_0, x_i)\left[ y_i - \alpha(x_0) - \beta(x_0)x_i \right]^2 \end{align*}\]

주의할 점은, 위 모델을 피팅할 때 전체 훈련데이터를 사용하였지만, 오직 \(x_0\)에 대해서만 예측을 진행한다는 것을 유의하자.

\(b(x)^T = (1,x)\)를 정의하여, $i$번째 행이 \(b(x_i)^T\)인 \(N \times 2\) desinged matrix \(\mathbf{B}\)를 정의하자. \(i\)번째 대각 성분이 \(K_{\lambda}(x_0, x_i)\)인 \(N \times N\) 행렬을 \(\mathbf{W}(x_0)\)라 하면, \(\hat{f}(x_0)\)을 다음과 같이 쓸 수 있다.

\[\begin{align*} \hat{f}(x_0) &= b(x_0)^T(\mathbf{B}^T\mathbf{W}(x_0)\mathbf{B})^{-1}\mathbf{B}^T\mathbf{W}(x_0)\mathbf{y} \\ &= \sum_{i=1}^N l_i(x_0)y_i \end{align*}\]

\(l_i(x_0)\)는 다음과 같으며, equivalent kernel이라고 불린다.

\[l_i(x_0) = \frac{\left[ \sum_jK(x_j, x_0)x_j^2 - x_0\sum_jK(x_j,x_0)x_j \right]K(x_i, x_0) + \left[ x_0\sum_jK(x_j, x_0) - \sum_jK(x_j,x_0)x_j \right]K(x_i, x_0)x_i}{\sum_jK(x_j, x_0)\sum_jK(x_j, x_0)x_j^2 - \left[\sum_jK(x_j,x_0)x_j\right]^2}\]

위 식을 통해 \(\sum_{i=1}^N l_i(x_0) = 1, \ \sum_{i=1}^N (x_i - x_0)l_i(x_0) = 0\)임을 알 수 있다.

다음 그래프는 \(x_0\)에 대한 equivalent kernel과 NW커널을 나타낸 것이다. (커널은 non-negative여야 하지만, 더 극명한 차이를 보이기 위하여 따로 0으로 처리하지 않았다.) 즉, 경계에서는 더 가까운 지점에서의 가중치를 크게 부여하여 편향을 줄여줌을 알 수 있다.

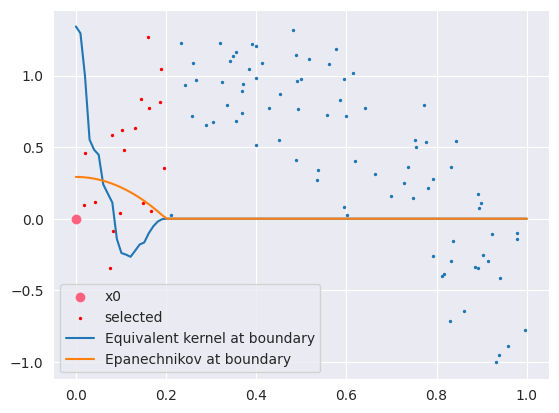
위의 그림에서 보았듯이, local linear regression은 자동으로 일차근사에 대하여 불편성을 갖도록 커널을 수정해주는 것을 알 수 있는데, 이를 automatic kernel carpentry라고 한다. 해당 성질에 대해 더 자세히 알아보자.

True function \(f\)에 대하여 평균이 0이고 등분산을 갖는 iid한 에러 모델을 가정하였을 때 \(\hat{f}\)의 기댓값은 테일러 근사를 이용하여 다음과 같이 나타낼 수 있다.

\[\begin{align*} \mathbb{E}\hat{f}(x_0) &= \sum_{i=1}^N l_i(x_0)f(x_i) \\ &= f(x_0)\sum_{i=1}^N l_i(x_0) + f'(x_0)\sum_{i=1}^N (x_i - x_0)l_i(x_0) + \frac{f''(x_0)}{2}\sum_{i=1}^N (x_i - x_0)^2l_i(x_0) + R \\ &= f(x_0) + \frac{f''(x_0)}{2}\sum_{i=1}^N (x_i - x_0)^2l_i(x_0) + R \end{align*}\]

즉, 편향은 \(\frac{f''(x_0)}{2}\sum_{i=1}^N (x_i - x_0)^2l_i(x_0) + R\)로 이차식 이상의 항들만 남는다는 것을 알 수 있다. 현재 시뮬레이션 데이터는 가운데 지점에서 이차식의 형태를 갖고 있으므로, local linear regression은 해당 구간에서 편향이 생김을 예상해 볼 수 있다. 이러한 현상을 trimming the hills라고 부른다. 다음은 local linear regression과 NW커널의 피팅 결과이다. 예상과 같이 가운데 지점에서도 선형으로 근사를 진행하기에 실제 이차형태보다 평탄하기에 예측이 좋지 않음을 볼 수 있다.

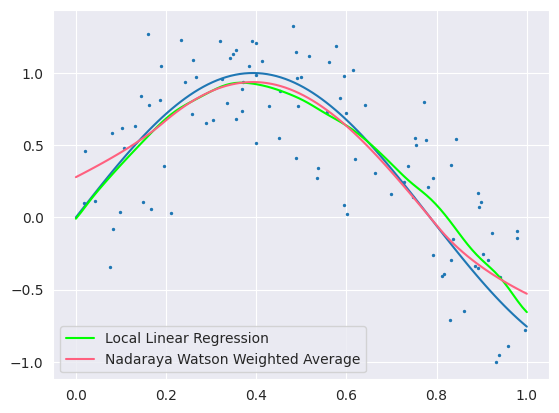
그렇다면 선형 근사가 아닌 더 높은 차수의 근사가 더 좋은 결과를 낼 것이라는 것은 이전에서와 같이 아님을 짐작해볼 수 있다. 물론, 위에서 보인 바와 같이 차수가 높아질 수록 편향은 줄어들지만, 분산이 반대로 증가하기 때문이다. 이에 대해서는 다음 local polynomial regression에서 일반화하여 증명할 것이다.

Local Polynomial Regression

Local linear regression을 다항식으로 확장한 방법으로 다음을 최소화하는 회귀계수를 찾아 회귀식을 세운다.

\[\underset{\alpha(x_0) \beta_j(x_0),j=1,...,d}{min} \sum_{i=1}^N K_{\lambda}(x_0, x_i)\left[ y_i - \alpha(x_0) - \sum_{j=1}^d\beta_j(x_0)x_i^j \right]^2\]

\(\hat{f}\)는 다음과 같다.

\[\hat{f}(x_0) = \hat{\alpha}(x_0) + \sum_{j=1}^d \hat{\beta}_j(x_0)x_j^j\]

다음은 local polynomial regression의 편향을 계산해보자.

\(b_j(x_0) = \sum_{i=1}^N (x_i - x_0)^jl_i(x_0)\)이라 할 때, 다항식의 차수를 \(k\)라고 한다면, \(b_j(x_0)\)은 \(j = 0\)일 때, $1$이고, 나머지의 경우에서 $0$이다. 이를 증명하기 위해 local linear regression에서와 같이 \(b(x)^T = (1,x, ..., x^k)\)라 정의하자. 마찬가지로, $i$번째 행이 \(b(x_i)^T\)인 desinged matrix \(\mathbf{B}\)와 \(i\)번째 대각 성분이 \(K_{\lambda}(x_0, x_i)\)인 대각행렬을 \(\mathbf{W}(x_0)\)를 정의해보자. 이를 이용하여 \(\hat{f}\)를 다음과 같이 쓸 수 있다.

\(\begin{align*} \hat{f}(x_0) &= b(x_0)^T(\mathbf{B}^T\mathbf{W}(x_0)\mathbf{B})^{-1}\mathbf{B}^T\mathbf{W}(x_0)\mathbf{y} \\ &= \sum_{i=1}^N l_i(x_0)y_i = \mathbf{L}^T\mathbf{y} \text{ where } \mathbf{L}^T = b(x_0)^T(\mathbf{B}^T\mathbf{W}(x_0)\mathbf{B})^{-1}\mathbf{B}^T\mathbf{W}(x_0) = \left( l_1(x_0), ... , l_N(x_0) \right) \end{align*}\) 여기서 \(\mathbf{L}^T\mathbf{B} = b(x_0)\)이기에 다음이 성립한다.

\[\begin{align*} \mathbf{L}^T\mathbf{B} &= \left(\sum_{i=1}^N l_i(x_0), ... , \sum_{i=1}^Nl_i(x_0)x_i^k \right) \\ &= \left(1, ..., x_0^k \right) = b(x_0) \end{align*}\]

첫번째 항을 보면 $j=0$인 경우는 증명이 되었다. 이제 \(j=1,...,k\)인 경우를 살펴보자. 마찬가지로 \(\mathbf{L}^T\mathbf{B} = b(x_0)\)의 마지막 원소를 이용하여 다음과 같이 보일 수 있다.

\[\begin{align*} \sum_{i=1}^N (x_i - x_0)^j l_i(x_0) &= \sum_{i=1}^N\sum_{k=0}^j {j \choose k}x_i^k(-x_0)^{j-k}l_i(x_0) \\ &= \sum_{k=0}^j {j \choose k}(-x_0)^{j-k}\sum_{i=1}^N x_i^k l_i(x_0) \\ &= \sum_{k=0}^j {j \choose k}(-x_0)^{j-k}x_0^k = 0 \end{align*}\]

따라서 \(k\)차 local polynomial regression의 편향은 \(k\)차 테일러 근사를 통해 다음과 같이 나타낼 수 있다.

\[\begin{align*} \mathbb{E}\hat{f}(x_0) - f(x_0) &= \sum_{i=1}^Nl_i(x_0)f(x_i) - f(x_0) \\ &= \left[f(x_0)\sum_{i=1}^Nl_i(x_0) + f'(x_0)\sum_{i=1}^N(x_i - x_0) + ... + \frac{f^k(x_0)}{k!}\sum_{i=1}^N(x_i - x_0) + R \right] - f(x_0) \\ &= f(x_0) + R - f(x_0) = R \end{align*}\]

다음은 분산에 대해 알아보자.

\[\begin{align*} \text{Var}\left[\hat{f}(x_0)\right] &= \text{Var} \left[\sum_{i=1}^N l_i(x_0)y_i \right] \\ &= \sum_{i=1}^Nl_i(x_0)^2\sigma^2 = \sigma^2\mathbf{L}^T\mathbf{L} \\ &= \sigma^2b(x_0)^T(\mathbf{B}^T\mathbf{B})^{-1}b(x_0) \end{align*}\]

분산의 경우, 차수인 \(k\)가 증가하면 마찬가지로 증가한다. 이를 증명하기 위해서는 다음을 보이면 충분하다.

\[b(x_0)^T(\mathbf{B}^T\mathbf{B})^{-1}b(x_0) \leq \left(b(x_0), x_0^{k+1} \right)^T\left( (\mathbf{B}, b)^T(\mathbf{B}, b) \right)^{-1}\left(b(x_0), x_0^{k+1} \right) \text{ where } b = (x_1^{k+1}, ..., x_N^{k+1})\]

여기서 우변의 가운데 항을 다음과 같이 쓸 수 있다. \(\left(\begin{matrix} \mathbf{B}^T\mathbf{B} & \mathbf{B}^Tb \\ b^T\mathbf{B} & b^Tb \end{matrix}\right)^{-1} \\ = \left(\begin{matrix} \left( \mathbf{B}^T\mathbf{B} \right)^{-1} + \left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb(b^tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1} & -\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb(b^Tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb)^{-1} \\ -(b^Tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb)^{-1}b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1} & (b^Tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb)^{-1} \end{matrix}\right)\)

\((b^Tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb)^{-1}\)는 실수로 이를 \(\alpha\)로 두고, \(N\)차원 벡터 \(\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb\)를 \(\beta\)라 쓰면 다시 다음과 같이 나타낼 수 있다.

\(\left(\begin{matrix} \mathbf{B}^T\mathbf{B} & \mathbf{B}^Tb \\ b^T\mathbf{B} & b^Tb \end{matrix}\right)^{-1}=\left(\begin{matrix} \mathbf{B}^T\mathbf{B} + \alpha\beta\beta^T & -\alpha\beta \\ -\alpha\beta^T & \alpha \end{matrix}\right)\) 따라서 이를 위의 우변에 대입하면 다음과 같다.

\[\begin{align*} \left(b(x_0), x_0^{k+1} \right)^T\left( (\mathbf{B}, b)^T(\mathbf{B}, b) \right)^{-1}\left(b(x_0), x_0^{k+1} \right) &= \left(b(x_0), x_0^{k+1} \right)^T\left(\begin{matrix} \mathbf{B}^T\mathbf{B} + \alpha\beta\beta^T & -\alpha\beta \\ -\alpha\beta^T & \alpha \end{matrix}\right)\left(b(x_0), x_0^{k+1} \right) \\ &= b(x_0)^T(\mathbf{B}^T\mathbf{B})^{-1}b(x_0) + \alpha\|x_0^{k+1} - b(x_0)^T\beta\|^2 \end{align*}\]

따라서, \(\alpha\)가 음이 아님을 보이면 충분하다.

\[\alpha = (b^Tb - b^T\mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^Tb)^{-1} = \left(b^T(\mathbf{I} - \mathbf{H})b\right)^{-1} \text{ where } \mathbf{H} = \mathbf{B}\left( \mathbf{B}^T\mathbf{B} \right)^{-1}\mathbf{B}^T\]

또한, \(\left(\mathbf{I} - \mathbf{H}\right)\)는 positive semi-definite이므로 \(\alpha\)는 $0$보다 크거나 같다.

 

Selecting the Width of Kernel

Kernel smoother 모델들의 파라미터는 훈련데이터셋과 커널의 너비를 조정하는 \(\lambda\)이다. 즉, 우리가 조절할 수 있는 파라미터는 \(\lambda\)가 전부이다. 너비가 증가할수록, \(\hat{f}\)는 더 많은 수의 훈련 데이터를 이용하여 추정을하기에 분산이 줄어들지만, 편향이 감소하는 경향이 있고, 반대로 너비가 감수할수록, 더 적은 수의 근방의 데이터들만으로 피팅을 진행하기에 더 지역적이 되기에 편향은 줄어들고, 반대로 분산이 증가하는 경향이 있다. 이후의 포스팅에서 다룰 \(C_p\), AIC, BIC과 같은 in-sample prediction이나 cross validation등을 이용하여 적절한 파라미터를 찾을 수 있다. Local regression의 경우 선형모델이기에 basis expansion에서 다룬, smoother matrix꼴을 이용하여 다음과 같이 효율적으로 LOOCV를 계산할 수 있다.

먼저, 훈련데이터들에 대한 피팅 값들의 벡터의 \(\hat{\mathbf{f}}\)를 smoother matrix를 이용하여 다음과 같이 나타낼 수 있다.

\[\begin{align*} \hat{\mathbf{f}} &= \left( \begin{matrix}b(x_1)^T \\ \vdots \\ b(x_N)^T \end{matrix}\right)(\mathbf{B}^T\mathbf{W}(x_0)\mathbf{B})^{-1}\mathbf{B}^T\mathbf{W}(x_0)\mathbf{y} \\ &= \left(\begin{matrix} l_1(x_1) & \cdots &l_N(x_1) \\ \ \vdots & \ddots & \vdots\\ l_N(x_1)& \cdots & l_N(x_N)\end{matrix}\right)\mathbf{y} = \mathbf{S}_{\lambda}\mathbf{y} \end{align*}\]

LOOCV는 다음과 같이 쓸 수 있다. 이는 Woodbury matrix identity를 이용하여 쉽게 보일 수 있다. Local regression만이 아닌 다른 선형모델들도 아래와 같이 효율적으로 LOOCV를 계산할 수 있다.

\[CV(\hat{\mathbf{f}}_{\lambda}) = \frac{1}{N}\sum_{i=1}^N (y_i - \hat{f}^{-i}(x_i))^2 = \frac{1}{N} \sum_{i=1}^N\left( \frac{y_i - \hat{f}(x_i)}{1 - \left\{S_{\lambda}\right\}_{ii}}\right)\]

 

Local Regression in \(\mathbb{R}^p\)

Nadaraya-Watson 커널 가중 평균과 local regression 모두 간단하게 \(p\)차원으로의 일반화가 가능하다. \(p=2, k=2\)인 local polynomial regression을 예로 들면, 입력 벡터를 \(b(X) = (1, X_1, X_2, X_1^2, X_2^2, X_1X_2)\)로 두고, 각 \(x_0 \in \mathbb{R}^p\)마다 다음 문제를 풀면 된다.

\(\underset{\beta(x_0)}{min} \sum_{i=1}^N K_{\lambda}(x_0, x_i)\left[ y_i - b(x_i)^T\beta(x_0) \right]^2\) \(\hat{f}\)는 다음과 같이 쓸 수 있다.

\[\hat{f}(x_0) = b(x_0)^T\hat{\beta}(x_0)\]

커널함수에서 거리를 계산하는 데에는 Euclidean norm을 사용해볼 수 있을 것이다. 이는 각 좌표축의 스케일에 영향을 받으므로, 커널을 계산하기 전에 독립변수들의 스케일링이 필요할 것이다. 이전에서도 살펴보았듯이, 데이터 간의 거리를 사용하는 모델들은 차원의 저주에 취약하며, local regression의 경우도 마찬가지이다. 위에서 보인 바와같이 1차원 독립변수의 경우 boundary effec문제가 발생하였는데, 이는 차원이 증가할록 boundary가 차지하는 부분이 커지는 차원의 저주와 결합하여 더 치명적으로 작용한다. 또한, 데이터의 차원 수에 비해 샘플의 수가 적다면, local regression은 적절한 보간을 해주지 못하기에 automatic kernel carpentry 효과도 의미가 없어진다. 이러한 경우에는 모델에 대한 추가적인 가정을 통하여 분석을 진행해주는 것이 좋다. 일반적으로 Local Regression은 4차원 이상의 데이터셋에 대해서는 그리 추천되지 않는다.

 

Structed Local Regression in \(\mathbb{R}^p\)

모델의 차원수에 비해 샘플사이즈가 적을 경우, 추가적인 structural assumption을추가해주는 방법이다. 이는 모델을 해석하는 데에도 이점이 있을 수 있다. Conditional plot을 예로 들어보자. 다음은 Ozone 데이터셋으로 종속 변수는 ozone conentration의 세제곱근이고, temperatrue, wind speed, radiation의 세가지 종속변수가 있다. 각각의 구간은 전체 데이터의 40%가 포함되도록 wind와 temperature의 구간을 나누어, x축을 radiation, y축을 종속변수로 산점도를 그려 데이터의 90%를 사용하도록 \(\lambda\)를 조절하여 Local linear regerssion을 진행한 결과이다. wind의 경우 행을 기준으로 행이 증가할수록 값이 감소하고, temperatured의 경우 열을 기준으로 열이 증가할수록 증가한다.

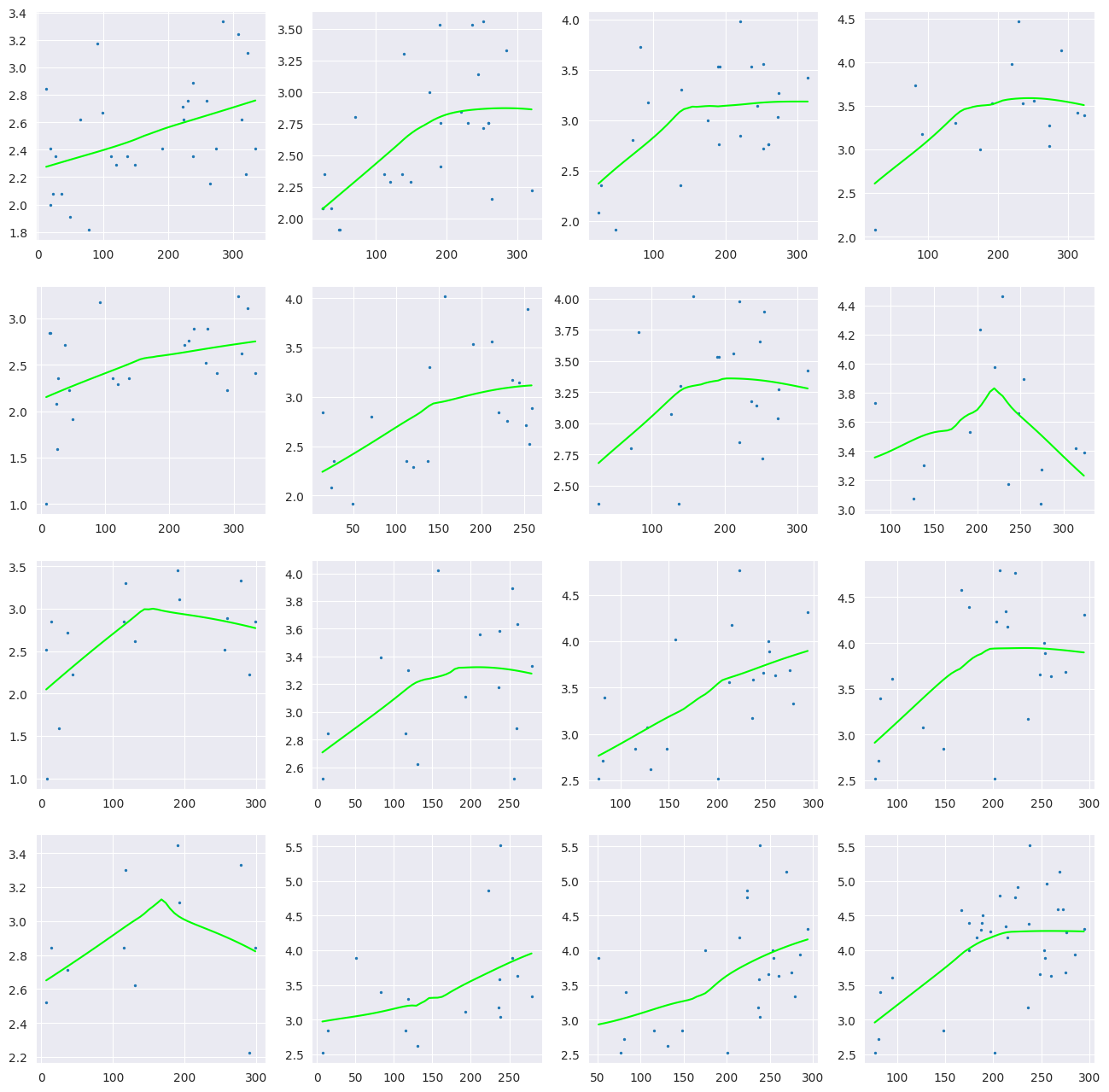
단순히, 세 개의 독립변수들을 이용하여 \(\mathbb{R}^3\)에서 local regression을 진행할 경우, 3개의 축과 한개의 종속변수 축으로하는 시각화를 할 수없지만, 위와 같이 2개의 독립변수를 조건부로 하는 1차원에서의 local regression이 해석력에서 이점이 있다.

Structured Kernels

위에서의 커널함수는 Euclidean norm을 사용하여 \(\sqrt{(x-x_0)^T(x-x_0)}\)를 이용하여 거리를 계산하기에 각 좌표축마다의 가중치가 동일하게 계산된다. 여기에 positive semidefinite 행렬 \(\mathbf{A}\)를 가중치 행렬로 사용하여 \(\sqrt{(x-x_0)^T\mathbf{A}(x-x_0)}\)로 좌표축마다의 다른 가중치의 거리를 계산할 수 있다. \(\mathbf{A}\)를 이용하여 특정 좌표축의 방향을 \(0\)으로 만들 수 있기에 일종의 제약조건을 줄 수도 있다. 단순히 대각행렬을 이용하여 특정 \(X_j\)의 방향을 \(\mathbf{A}_{jj}\)를 이용하여 조정할 수 있다. 즉, low-rank를 갖는 \(\mathbf{A}\)는 ridge regression의 효과를 내포하고 있다. 또한 이미지와 신호 데이터와 같이 상관관계가 높은 데이터의 경우, 공분산 행렬 \(\Sigma\)를 이용하여 마할라노비스 거리를 통해 커널함수를 계산할 수 있다.

Structured Regression Functions

또한 interaction effect를 고려한 회귀모델을 가정해 볼 수 있다. 즉 다음과 같이 ANOVA decompositon꼴의 모델을 가정해보자.

\[\mathbb{E}\left(Y|X\right) = f(X_1,...X_p) = \alpha + \sum_j g_j(X_j) + \sum_{k<l} g_{kl}(X_k,X_l) + ...\]

Additive model의 경우 main effect항만을 고려하기에 \(f(X) = \alpha + \sum_{j=1}^p g_j(X_j)\)로 쓸 수 있고, Second-order model의 경우 최대 두개의 interaction effect를 고려한다. Low-order interaction 모델의 경우 9장에서 제시될 backfitting 알고리즘을 이용하여 iterative하게 구현이 가능하다. Additive model을 예로 들면, 먼저 \(\hat{\alpha} = \bar{y}, \hat{g}_j(X_j) =0\)로 초기화하여, 매 iteration마다 \(k\)번째 항을 제외하고 나저미 항이 알려졌다고 가정하여, \(\{ (x_i, y_i - \hat{\alpha} - \sum_{k \neq j} \hat{g}_j(X_j)): i=1,..,N \}\)를 이용하여 \(\hat{g}_k\)를 추정한다. 즉 매 interation마다 1차원에서의 local regression을 진행하는 것과 같다. 이를 각 항들이 특정 값에 수렴할 때 까지 반복한다.

또 다른 방법으로는 varying coefficient model이 있다. 이는 \(p\)차원 독립변수에서 \((X_1, ... ,X_q) \ (q<p)\)만을 이용하여 선형 모델을 가정하는데 회귀 계수들은 나머지 독립변수들을 조건부로 하는 데이터셋 \(Z\)에 대한 함수로 추정한다. 즉 다음과 같이 조건부로 선형모델을 가정한다.

\[f(X) = \alpha(Z) + \beta_1(Z)X_1 + ... + \beta_q(Z)X_q\]

\(Z\)가 주어졌을 때, 이는 선형모델이지만, 각각의 회귀계수는 \(Z\)에 따라 달라진다. 회귀계수는 위에서처럼 locally weighted least squares를 이용하여 다음과 같이 계산한다.

\[\underset{\alpha(z_0) \beta(z_0)}{min} \sum_{i=1}^N K_{\lambda}(z_0, z_i)\left[ y_i - \alpha(z_0) - \sum_{j=1}^q\beta_q(z_0)x_{qi} \right]^2\]

위에서 보인 Conditional plot이 varying coefficient model의 예시이다. wind와 temperature의 구간에 따라 달라지는 회귀계수를 이용하여 분석을 진행할 수 있다.

 

Local Likelihood and Other Models

local regression과 varying coefficient model 모두 가중치를 부여할 수 있는 parametric model에 적용이 가능할만큼 확장성이 용이하다. likelihood model의 경우, \(l(\beta) = \sum_{i=1}^N l(y_i, \theta(x_i))\)를 최대화하는 파라미터를 추정량으로 사용하였다. linear model의 경우 \(\theta(x_i) = x_i^T\beta\)로 이를 \(l(\beta)\)를 최대화하는 \(\beta\)를 찾는다. 이를 localization을 하면 다음과 같이 쓸 수 있다.

\[l(\beta(x_0)) = \sum_{i=1}^N K_{\lambda}(x_0, x_i)l(y_i, x_i^T\beta(x_0))\]

varying coefficient model의 경우 다음과 같다.

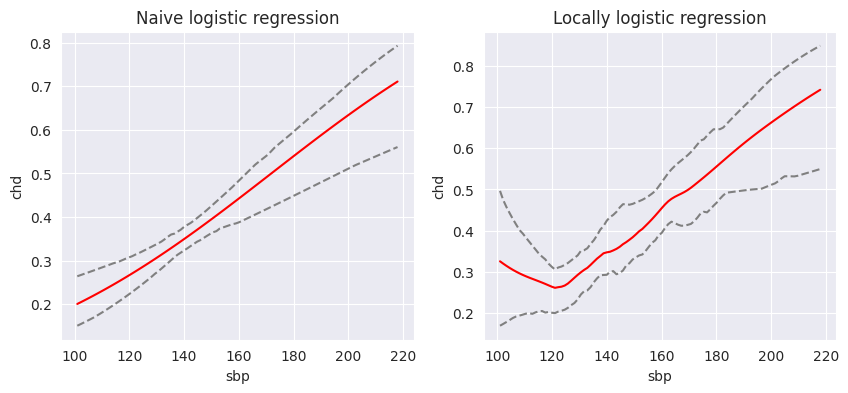
\[l(\theta(z_0)) = \sum_{i=1}^N K_{\lambda}(z_0, z_i) l(y_i, \eta(x_i, \theta(z_0)))\]

linear model의 경우 \(\eta(x_i, \theta(z_0)) = x^T\theta\)로 둘 수 있다. 다음은 South Afirica Heart Disease 데이터셋에서 종속변수 chd와 독립변수 sbp를 이용하여 각각 왼쪽이 logistic regression, 오른쪽이 locally logistic regression를 진행하여 \(p_i\)를 추정한 그래프이다. 신뢰구간은 non-paramteric bootstrap을 이용하여 95%의 신뢰구간을 구한 그림이다. 단순 logistic regression보다 더 유연하다는 것을 확인할 수 있다.