[ESL 리뷰] 교재 5장-2 Basis Expansion and Regularization in multivariate case

이번 포스팅에서는 저번 포스팅에 이어서 이번에는 다차원으로 확장한 Tensor product splines, Thin plate spines, 그리고 RKHS에 대하여 살펴볼 예정이다.

 

Intro

이전 포스팅에서의 스플라인의 정의를 다시 살펴보자. Univariate인 경우에서 knot \(\xi_1 < ... < \xi_K\)에 대하여

• \(f\)는 각 구간 \((-\infty, \xi_1], [\xi_1,\xi_2],...,[\xi_K,\infty)\)에서 \(M\)차 다항식이다.
• \(l=0,...,M-1\)에 대해 \(f^{(l)}(x)\)은 \(\xi_1, ..., \xi_K\) 에서 연속이다.

를 만족하여야 했다. 이를 다차원으로 확장하면 두번째 조건을 \(f \in C^{K-1}\) (\(C^{K-1}\)은 \(K\)보다 작은 모든 차수의 미분에 대하여 연속인 함수들의 집합) 으로 수정하면 될 것이다. 하지만 이러한 정의는 \(X \in \mathbb{R}^d\)가 2차원인 즉, \(d = 2\)인 경우에서부터 문제가 발생한다. 사실 이번 포스팅에서 살펴볼 Tensor product splines 와 Thin plate spline, 그리고 사용되는 다른 많은 모델들도 진정한 의미의 spline 곡선이 아니다. 다차원에서의 spline을 만들어주는 basis function을 찾기가 힘들기 때문인데, 심지어 다차원에서는 spline을 정의하는것 조차도 힘들다. 이를 확인하기 위해 먼저, \(d\) 차원에서의 \(k\) 차 다항식의 형태를 고려해보자면 다음과 같을 것이다.

\[f(x) = \sum_{|\alpha|\leq k} \beta_{\alpha} \prod_{i=1}^d x_i^{\alpha_i}\]

위 식에서 \(\beta_{\alpha}\)는 coefficient 항이고, \(\alpha = (\alpha_1, ... ,\alpha_d) \in \mathbb{Z}^d_+\)로 각 항의 차수를 나타내준다. 즉, parameter인 coefficient 항의 개수는 \((d+1)\)개에서 중복을 허용하여 \(k\)개를 뽑는 것과 같으므로 \(_{d+1}H_k = _{d+k} C_k\) 개이다.

\(d=2\)인 경우의 cubic splines을 고려해보자. 다차원에서의 piece wise polynomail에서 이러한 piece를 간단하게 삼각형 꼴로 생각해서 논의를 이어나가 보자. 사실 이 경우, \(C^2\)에 속하는지 확인하기도 이전에, 이미 \(C^1\) 관한 제약조건을 설정하는데에서 문제가 발생한다. 인접한 edge \(e\)를 공유하는 두 개의 삼각형을 생각해보자. \(d=2, \ k=3\) 이므로 각각의 파라미터수는 \(_{3}H_3 = 10\) 으로, 총 20개의 파라미터가 있다. 또한, \(C^1\) 관한 제약조건은 위 두개의 삼각형으로 만들어진 \(f,g\)에 대하여

\[\forall x \in e, \forall |\alpha|\leq1, \ f^{(\alpha)} (x) = g^{(\alpha)}(x)\]

이다. 즉, 10개의 파라미터가 제약조건에 포함된다. 이를 그림으로 나타내면 다음과 같다. 각 점들은 coefficient가 할당되는 곳이고, 빨간색 점은 자유로운 파라미터, 하얀색 점은 제약조건에 의해 고정되는 부분이다. 회색으로 칠해진 부분이 \(C^1\) 제약조건에 영향을 받는 부분이다.

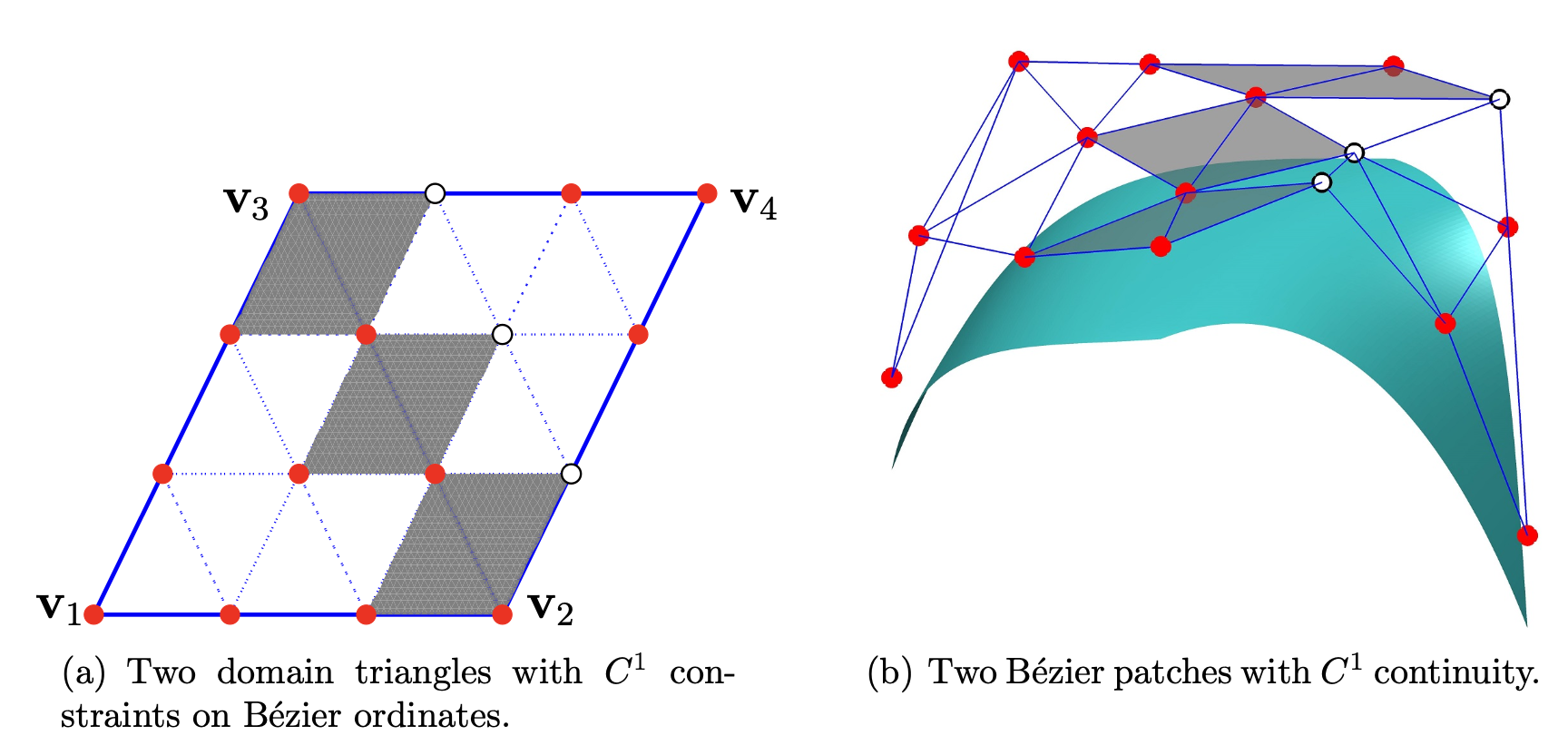
위와 같이 선형 제약조건들이 모두 얽혀있기 때문에 이를 만족하는 paramter 집합이 존재하는지 불분명하다. 이러한 문제를 해결하기 위해서는 다항식의 차수 \(k\)를 증가시켜야 한다. \(C^s\)의 제약조건을 만족시키기 위해서는 \(k\)가 \(s(d+1) + d\)보다 크거나 같아야 함이 알려져 있다. 즉, 2차원에서는, 이를 만족하는 최소 차수가 5이고, \(d=3\)인 경우에는 7이다. 이는 굉장히 파라미터를 낭비하는 것처럼 보인다.

 

Tensor product Splines

먼저, 텐서곱이 무엇인지 정의를 해보자. 임의의 함수 \(f_1,...,f_p\)에 대하여, 다음과 같은 다변수 함수 \(f_1 \otimes ... \otimes f_p: \mathbb{R}^p \rightarrow \mathbb{R}\) 를 텐서곱이라고 정의한다.

\[f_1 \otimes ... \otimes f_p (x_1,...,x_p) = \prod_{i=1}^p f_i(x_i)\]

즉, \(d\) 차원에서 \(K\) 개의 knot \(\xi_1,...,\xi_K\)를 갖는 차수가 \(M\)인 spline 곡선을 가정한다고 할때, 각 차원에서의 basis function들을 \(h_1,..., h_{N} \ (N = M + K + 1)\)이라고 한다면, Tensor product splines를 다음과 같이 정의할 수 있다.

\[f(x) = \sum_{j \in \{ 1,...,N\}^d} \beta_j h_{j_1}(x_1)\otimes ... \otimes h_{j_d}(x_d)\]

즉, 각 차원마다의 basis function들을 1개씩 뽑아 모든 조합을 곱하여 더한 것이다. 즉 \(h_{j_1}(x_1)\otimes ... \otimes h_{j_d}(x_d)\)를 하나의 basis function으로 볼 수 있다. \(f\)는 각 hyper cube \([\xi_{j_1}, \xi_{j_1+1}] \times ... \times [\xi_{j_d}, \xi_{j_d +1} ]\)에서는 분명히 다항식이지만, 반드시 차수가 \(M\)일 것이라는 보장은 없다. Tensor product spline \(f\)의 차수를 강조하기 위해서 다음과 같이 나타내 볼 수 있다.

\[f(x) = \sum_{\alpha_1, ... \alpha_d \leq M} \beta_{\alpha} \prod_{i=1}^d x_i^{\alpha_i}\]

즉, 이는 앞에서 정의한 \(d\)차원에서의 \(M\)차 다항식의 형태와 다르나는 것을 알 수 있다. 다음 그림은 \(d=2\)인 경우의 텐서곱을 이용한 cubic spline의 basis fucntion을 나타낸 것이다.

 

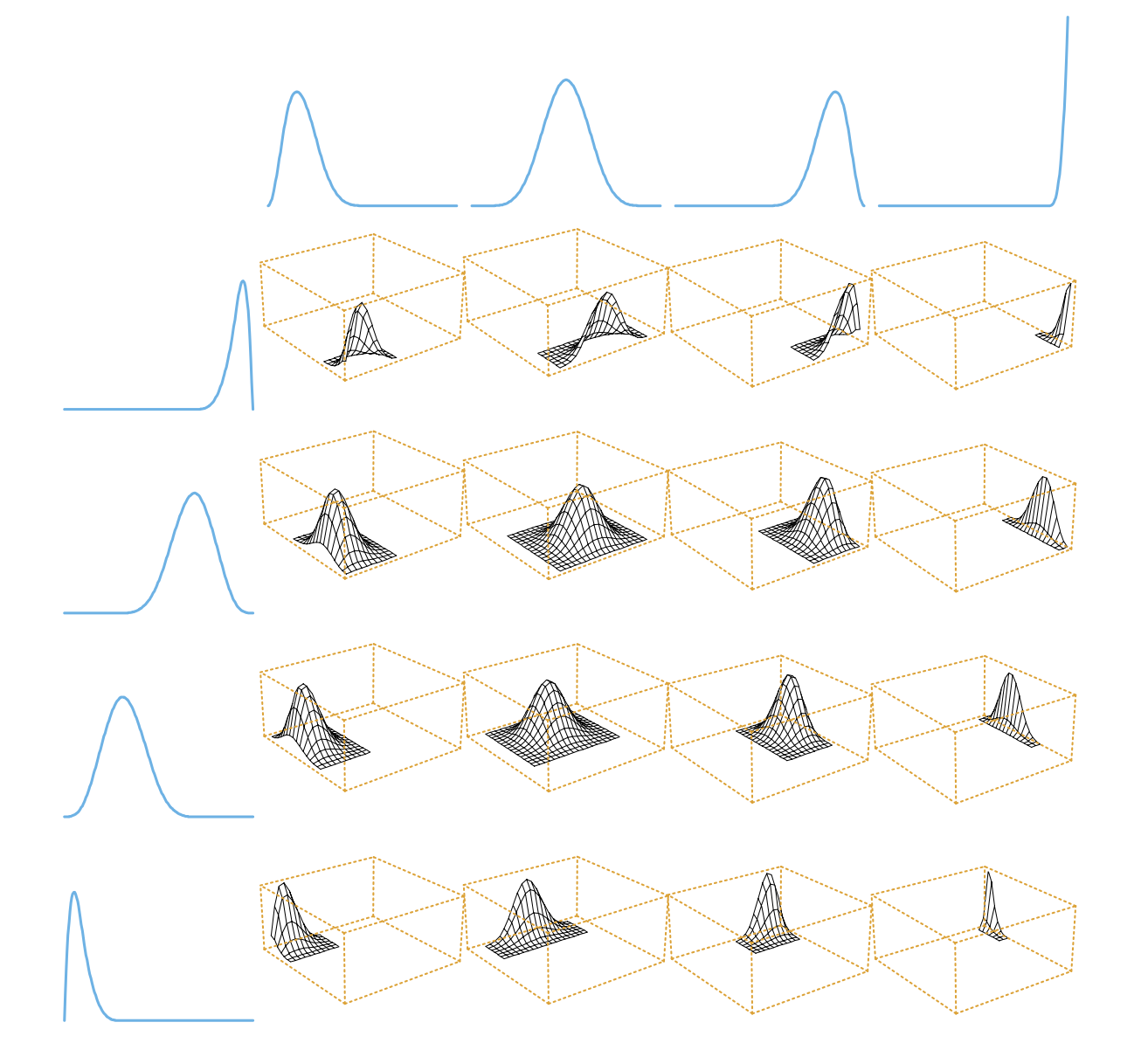
Thin plate Splines

이전의 Smoother splines과 같이 먼저, 다음과 같은 최적화 문제를 생각해보자.

\[\underset{f \in \mathcal{H}}{\text{min}} \sum_{i=1}^N (y_i - f(x_i))^2 + \lambda \int_U \sum_{|\alpha|=m}\left[D^{\alpha}f(x)\right]^2dx\]

\(m\)은 자연수이고, \(U\)는 \(x_1, ... , x_N\)를 포함하는 \(\mathbb{R}^d\)의 부분집합이고, \(\mathcal{H}\)는 두번째 항이 정의될 수 있는 유한한 함수공간으로, \(W^{m,2}(U)\)로 \(L^2(U)\)에 존재하는 함수중에 \(|\alpha| \leq m\) 인 \(\alpha\)에 대해 \(\alpha\)-th weak derivative인 함수들의 공간이다. 위 문제는 \(2m > d\)일 경우 해가 존재하는 well-defined인 경우이고, 이 때의 해를 Thin plate splines라고 한다. 반대는 해가 없는 ill-defined인 경우이다. Sobolev embedding theorem에 의해 이러한 결과가 도출된다.

 

Sobolev embedding theorem

Sobolev embedding theorem에서 \(2m >d\)인 경우는, the supercritical regime 으로 \(W^{m,2}(U)\) 가 Hölder splace \(C^{r+\gamma}\) (\(L^{\infty}(U)\)에 대해 \(|\alpha| \leq r+\gamma\) 를 만족하는 \(\alpha\)-계도함수가 bounded이고 \(|\alpha| = r+\gamma\) 인 \(\alpha\)-계도함수가 립시츠 연속인 함수들의 집합)로 continuously embeded된다.

countinously embeding은 두 normed space간의 inclusion function이 연속인 경우로 이때의 두 공간의 norm은 almote equivalent이다. inclusion function은 정의역이 공역의 부분집합이며, 정의역의 모든 원소를 자신으로 대응시키는 함수로 수식으로 나타내면 다음과 같다.

\(X \subset Y\)인 두 집합 \(X,Y\)에 대하여, inclusion function \(\iota_{X,Y}\)는 다음을 만족하는 함수이다.

• \(\iota_{X,Y}: X \rightarrow Y\) ( \(X \hookrightarrow Y\) )
• 임의의 \(x \in X\)에 대하여, \(\iota_{X,Y} (x) = x\)

즉, \(X \subset Y\)이며, 각각 norm \(\| \cdot \|_X, \ \| \cdot \|_Y\)을 갖는 normed space \(X,Y\)에 대하여 inclusion map \(i: X \hookrightarrow Y\)가 연속, 즉 다음을 만족할 때, \(X\)가 \(Y\)로 continously embeded되었다고 한다.

\[\forall x\in X, \ \exists C>0 \text{ s.t. } \|x\|_Y \leq C\|x\|_X\]

이는 즉, \(C^0(U)\)에도 continuously embed되었고 해당 공간은 \(L^{\infty}\) norm을 갖는 연속인 함수들의 집합이다. 따라서 \(\| \cdot \|_{W^{m,2}(U)}\) 와 \(\| \cdot \|_{\infty}\)가 almost equivalent하므로, 함수열 \(f_k\)에 대하여 \(k \rightarrow \infty\)일 때, \(\|f_k - f\|_{W^{m,2}(U)}\)은 곧, \(\|f_k-f\|_{\infty}\)을 의미한다. 이는 즉, \(f_k(x) \rightarrow f(x), \ \forall x\) 인 균등수렴을 의미한다.

 

\(d=2\) case

\(d=2\) 인 경우 차수를 2로 설정하면 supercritical regime에 해당하므로 해가 존재한다고 할 수 있다. 즉, 패널티항을 다음과 같이 쓸 수 있다.

\[\underset{f \in \mathcal{H}}{\text{min}} \sum_{i=1}^N (y_i - f(x_i))^2 + \lambda \int_{\mathbb{R}^2} \left[ \left(\frac{\partial^2 f(x)}{\partial x_1^2} \right) + \left(\frac{\partial^2 f(x)}{\partial x_1x_2} \right) + \left(\frac{\partial^2 f(x)}{\partial x_2^2} \right)\right]^2dx\]

이와 비슷한 smoother splines에서와 같이, 해당 문제에서도 유한하며 유일한 해가 존재하지만, 차이점은 위 문제는 \(U\)에 의해 해가 달라질 수 있다. 위와 같이 \(U = \mathbb{R}^2\)라면, 다음과 같은 해가 도출된다.

\[f(x) = \beta_0 + \beta^Tx + \sum_{j=1}^N \alpha_jh_j(x), \\ \text{where } h_j(x) = \|x - x_j\|^2 \log\|x-x_j\|\]

위 식의 \(h_j(x)\) 를 radial basis function의 한가지 예이다. 즉 \((1+2+N)\)개의 파라미터를 가진다. 다음 조건은 문제를 유한 차원으로 제한하는 필요충분 조건이다.

\[\sum_{i=1}^N \alpha_i = \sum_{i=1}^N \alpha_ix_i = 0\]

따라서 자유로운 파라미터의 수는 \(N+3 - 3 = N\) 으로 \(N\)개이다.

 

Reproducing Kernel Hilbert Space

RKHS를 정의하기 전에 먼저 Hilbert space와 kernel 에 대해서 각각 알아보자.

 

Hilbert space

Hilbert space \(\mathcal{H}\)는 내적에 대하여 complete한 함수 공간이다. (즉, \(m,n \rightarrow \infty\)이면, \(\|f_m - f_n\|_{\mathcal{H}} \rightarrow 0\)) 내적에 대한 정의를 복습해보자면, 실수체를 갖는 \(\mathcal{H}\)에 대하여, 내적 \(\left<\cdot,\cdot \right>_{\mathcal{H}} : \mathcal{H} \times \mathcal{H} \rightarrow \mathbb{R}\)은 임의의 \(\forall f,g,h \in \mathcal{H}, \ \forall c \in \mathbb{R}\)에 대하여 다음을 만족하는 함수이다.

1. \[\left< f+h, g \right>_{\mathcal{H}} = \left< f, g \right>_{\mathcal{H}} + \left< h, g \right>_{\mathcal{H}}\]
2. \[\left< cf, g \right>_{\mathcal{H}} = c\left< f, g \right>_{\mathcal{H}}\]
3. \[\left< f, g \right>_{\mathcal{H}} = \left< g, f \right>_{\mathcal{H}}\]
4. \[\left< f, f \right>_{\mathcal{H}} > 0 \text{ if } f \neq 0\]

 

내적의 성질으로는 내적을 통하여 항상 norm \(\|\cdot\|_{\mathcal{H}}\)을 다음과 같이 정의할 수 있다.

\[\|f\|^2_{\mathcal{H}} = \left<f, f\right>_{\mathcal{H}}\]

 

Note.

1. 임의의 Hilbert space는 또한 norm에 대하여 complete한 Banach space이다. (단 ,역은 성립하지 않는다.)
2. \(f_n \rightarrow f\)가 임의의 \(x\)에 대해 \(f_n(x) \rightarrow f(x)\)를 내포하지 않는다. (단, 이는 RKHS에서 성립한다.)

 

Kernel

함수 \(k: \mathcal{X} \times \mathcal{X} \rightarrow \mathcal{R}\)에 대해 다음을 만족하는 map \(\phi : \mathcal{X} \rightarrow \mathcal{H}\)가 존재할 때, \(k\)를 kernel 이라고 정의한다.

\[\forall x,y \in \mathcal{X}, \ k(x,y) = \left< \phi(x), \phi(y) \right>_{\mathcal{H}}\]

내적에 정의에 의해서 kernel \(k\)는 항상 음이아닌 값을 갖고 있고, symmetric임을 알 수 있다. 또한 임의의 \(x_1, ... , x_N \in \mathcal{X}\)에 대해서 \(\{ K \}_{ij} = k(x_i,x_j)\)를 원소로 갖는 \(N \times N\) 행렬을 \(K\)라고하자. 모든 \(a \in \mathbb{R}^N\)에 대해서

\[a^TKa = \sum_{i,j} a_iK(x_i,x_j)a_j = \sum_{i,j} \left< a_i\phi(x_i),a_j\phi(x_j) \right> \geq 0\]

이므로, \(K\)는 positive semi-definite이다. 이러한 성질 때문에 \(k\)를 positive semi definite라고 부르기도 한다. 즉, kernel은 항상 positive semi-definite이다. 흥미로운 점은 역으로, 임의의 positive semi-definite 함수 \(k: \mathcal{X} \times \mathcal{X} \rightarrow \mathcal{R}\)는 kernel이다. 즉, positive semi-definite임을 확인하면, \(\phi\)를 찾을 필요 없이 바로 kernel임을 알 수 있다.

( \(\mathcal{X} = \mathbb{R}^d\)일 때, kernel의 예시 )

• Polynomial kernel: \(k(x,y) = (1+x^Ty)^m\)
• Exponential kernel: \(k(x,y) = \exp(x^Ty)\)
• Gaussian kernel: \(k(x,y) = \exp(-\|x-y\|^2_2 / \sigma^2)\)

 

Reproducing kernel Hilbert space

kernel \(k\)를 갖는 Hilbert space \(\mathcal{H}\)에 대하여, 다음 조건을 만족하는 \(\mathcal{H}\)를 reproducing kernel Hilbert space(RKHS)라고 부른다.

1. \(\forall x \in \mathcal{X} \ k(\cdot, x) \in \mathcal{H}\) (reproducers of evaluation)
2. \(\forall f \in \mathcal{H}, \left< f, k(\cdot, x)\right>_{\mathcal{H}} = f(x), \ x \in \mathcal{X}\) (reproducing property)

 

Reproducing propery에 의해서 다음이 성립한다.

\[\forall x,y \in \mathcal{X}, \ \left< k(\cdot,x), k(\cdot,y)\right>_{\mathcal{H}} = k(y,x) = k(x,y)\]

즉, \(\phi(x) = k(\cdot, x)\)를 \(k\)의 map으로 볼 수 있다.

\(x \in \mathcal{X}\)에 대해 \(\delta_x : \mathcal{H} \rightarrow \mathbb{R}\)를 evaluation operator라고 하자. 즉, \(\delta_x(f) = f(x)\)이다

 

Note. evaluation operator는 linear하다.

• \[\forall f,g \in \mathcal{H}, \ \delta_x(f+g) = (f+g)(x) = f(x) + g(x) = \delta_x(f) + \delta_x(g)\]
• \[\forall a \in \mathbb{R}, \ \forall f \in \mathcal{H}, \ \delta_x(af) = af(x) = a\delta_x(f )\]

 

evaluation operator를 정의하면, Hilbert space \(\mathcal{H}\)의 모든 evaluation operator가 연속일 경우를 RKHS의 정의로 사용할 수 있다. 즉,

\[\forall x\in \mathcal{X}, \ \forall f\in\mathcal{H}, \exists M < \infty \text{ s.t. } |\delta_x(f)| = |f(x)| \leq M \|f\|_{\mathcal{H}}\]

Sobolev space \(W^{m,2}(U)\) (\(U \subset \mathbb{R}^d\))는 Hilbert space이다. 또한 \(2m > d\)인 supercritical regime에서 the point evaluation operator가 연속임을 확인하였다. 즉, \(W^{m,2}(U)\)가 RKHS일 필요충분조건은 \(2m > d\)이다. 그렇다면 \(2m > d\)에서 Sobolev space의 kernel은 어떻게 될까? 만약, \(U = \mathbb{R}^d\)일 경우 kernel \(k\)는

\[k(x,y) = \int \frac{\exp(2\pi i (x-y)^Tu}{1 + \sum_{0 \leq | \alpha | \leq m} \prod_{j=1}^d(2 \pi u_j)^{2\alpha_j}}\]

이다. 만약 \(d=1, m=2\)라면 \(k\)는 다음과 같다.

\[k(x,y) = \frac{1}{\sqrt{3}}\exp\left(-\frac{\sqrt{4}|x-y|}{2}\right) \sin \left( \frac{|x-y|}{2} + \frac{\pi}{6} \right)\]

즉, 이전 포스팅에서 다뤘던, smooting splines에서의 equivalent kernel과 상수배를 제외하면 같음을 알 수 있다. 이를 smoothing spline kernel라고 부른다. 또한 \(d=2, m=2\)인 경우에 \(k\)는 다음과 같다.

\[k(x,y) = \frac{1}{16\pi} \|x-y\|^2_2 \log\|x-y\|^2_2\]

이는 \(d=2\)인 경우의 thin plate splines의 basis function과 유사하다. 따라서 이를 thin plate spline kernel라고 부른다.

 

Riesz Representation Theorem

이번에는 위에서 확인한 evaluaion operator의 연속성이 처음 정의한 reproducing propery와 어떻게 대응되는지를 확인해보자. 먼저 Hilbert space \(\mathcal{H}\)는 topological vector space이므로, dual \(\mathcal{H}^*\)는 continuous linear operator들의 집합이다.

(Riesz Representation Theorem) 임의의 \(\rho \in \mathcal{H}^*\)에 대해 다음을 만족하는 \(f_{\rho} \in \mathcal{H}\)가 유일하게 존재하며, 이를 \(\rho\)의 Riesz representation라고 부른다.

\[\forall h \in \mathcal{H}, \ \rho(h) = \left<h, f_{\rho}\right>_{\mathcal{H}}\]

즉, 모든 linear operator의 값을 \(\mathcal{H}\)내 다른 원소와의 내적으로 표현할 수 있다는 말이다. 증명과정은 다음과 같다.

 

(증명)

\(f_{\rho}\)의 존재성만을 증명해보자. \(\rho\)의 영공간을 \(K\)라고 정의하자. 즉 \(K = \{ m \in \mathcal{H}: \rho(m) = 0 \}\). 만약 \(K = \mathcal{H}\)라면, \(f_{\rho}\)를 0으로 두면 된다. 이번에는 \(K \subset \mathcal{H}\)일 때를 고려해보자. \(K = \rho^{-1}(\{ 0 \})\)이고 \(\{ 0 \}\) 은 \(\mathbb{R}\)에서 closed set이고, \(\rho\)가 연속이므로, \(K\)도 \(\mathcal{H}\)의 closed subspace이다. 즉, \(\mathcal{H} = K\oplus K^{\perp}\)로 나타낼 수 있다. 또한 \(K\)가 \(\mathcal{H}\)의 부분집합이므로, \(K^{\perp}\)는 공집합이 아니다. 따라서 \(p \in K^{\perp} ( p \neq 0)\)이 존재하여, 다음이 성립한다.

\[\forall h \in \mathcal{H}, \rho \left[ (\rho h)p - (\rho p) h\right] = (\rho h)(\rho p) - (\rho p)(\rho h) = 0\]

따라서 \((\rho h)p - (\rho p) h\)가 \(K\)에 속하므로,

\[\left< p, (\rho h)p - (\rho p) h \right>_{\mathcal{H}} = (\rho h)\|p\|_{\mathcal{H}}^2 - (\rho p)\left< p,h \right> = 0\]

이다. 즉, \(\rho h = \frac{(\rho p)\left< p,h \right>}{\|p\|_{\mathcal{H}}^2} \ \forall h \in \mathcal{H}\) 가 성립하므로, \(f_{\rho} = \frac{\rho p}{\|p\|_{\mathcal{H}}^2}p\) 라 하면, 존재성을 증명할 수 있다.

 

따라서 모든 evaluation operator가 linear임은 위에서 확인했으므로, 연속성 또한 만족한다면 Riesz Representation Theorem에 의해 riesz representation \(f_{\rho}\)가 존재하므로, reproducing property가 만족함을 알 수 있다.

 

Representer Theorem

\(\mathcal{H}\)를 kernel \(k: \mathcal{X} \times \mathcal{X} \rightarrow \mathcal{R}\)를 갖는 RKHS라고 하고, 다음과 같은 무한 차원의 문제를 생각해보자.

\[\underset{f \in \mathcal{H}}{\text{argmin}} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda \|f\|^2_{\mathcal{H}}\]

\(\| \cdot \|_{\mathcal{H}}\)는 내적으로 정의한 norm이고, 가장 많이 사용되는 kernel \(k\)는 위에서 언급한 polynomial kernel, exponential kernel, gaussian kernel등이 있다. 흥미로운 점은 위 문제는 다음과 같이 kernel에 대한 선형결합으로 유일한 유한차원의 해를 갖는다.

\[f(x) = \sum_{i=1}^N c_i k(x,x_i) \text{ where } c_1,...,c_N \in \mathbb{R}\]

 

(증명)

\(\mathcal{H}_0 = \text{span}\{ k(\cdot,x_1), ..., k(\cdot,x_N) \}, \ \mathcal{H}_1 = \{ f \in \mathcal{H}: f(x_1) = ... = f(x_N) = 0 \}\)이라고 하자. reproducing property에 의해서 임의의 \(f \in \mathcal{H}_1\)에 대해

\[\left< f, k(\cdot, x_i) \right>_{\mathcal{H}} = f(x_i) = 0, \ i=1,...,N\]

을 만족한다. 따라서 \(\mathcal{H}_0\)에 속하는 임의의 함수 \(g = \sum_{j=1}^N c_jk(\cdot, x_j)\)에 대하여 다음을 만족한다.

\[\left< f, g \right>_{\mathcal{H}} = \left< f, \sum_{j=1}^N c_jk(\cdot, x_j) \right>_{\mathcal{H}} = \sum_{j=1}^N c_jf(x_j) = 0\]

즉, \(\mathcal{H}_1\)은 \(\mathcal{H}_0\)의 orthgonal complement이다. 따라서 \(\mathcal{H} = \mathcal{H}_0 \oplus \mathcal{H}_1\)으로 나타낼 수 있다. 즉 임의의 함수 \(f \in \mathcal{H}\)에 대해 \(f = f_0 + f_1\) 을 만족하는 \(f_0 \in \mathcal{H}_0, \ f_1 \in \mathcal{H}_1\)가 존재한다. 따라서 다음이 성립한다.

\[\begin{align*} \sum_{i=1}^N L(y_i, f(x_i)) &= \sum_{i=1}^N L(y_i, f_0(x_i)) \\ \|f\|^2_{\mathcal{H}} &= \|f\|^2_{\mathcal{H}_0} + \|f\|^2_{\mathcal{H}_1} \\ \end{align*}\]

이를 위 문제에 대입하면 다음과 같다.

\[\begin{align*} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda \|f\|^2_{\mathcal{H}} &= \sum_{i=1}^N L(y_i, f_0(x_i)) + \lambda \left( \|f\|^2_{\mathcal{H}_0} + \|f\|^2_{\mathcal{H}_1} \right) \\ &\geq \sum_{i=1}^N L(y_i, f_0(x_i)) + \lambda |f\|^2_{\mathcal{H}_0} \end{align*}\]

즉, 등호는 \(f\)가 \(\mathcal{H}_0\)에 속할때에만 해당되기에 유일성이 보장되고, \(f_0\)은 \(\{ k(\cdot,x_1), ..., k(\cdot,x_N) \}\)의 선형결합이므로 \(f(x) = \sum_{i=1}^N c_i K(x, x_i)\)이다.

 

이제 이를 최적화 문제에 대입해보자. 먼저, reproducing property에 의해 다음이 성립한다.

\[\|f\|_{\mathcal{H}}^2 = \sum_{i,j}c_ic_j\left< k(\cdot, x_i), k(\cdot, x_j)\right>_{\mathcal{H}} = \sum_{i,j}c_ic_jk(x_i,x_j)\]

따라서, real vector \(c=(c_1,...,c_N)\)를 파라미터로 갖는 다음과 같은 문제로 다시 쓸 수 있다.

\[\underset{c}{\text{min}} L(\mathbf{y}, Kc) + \lambda c^TKc\]

즉 적절한 loss function \(L\)과 kernel \(k\)를 선택하여 위 문제를 풀 수 있다.