[ESL 리뷰] 교재 5장-1 Basis Expansion and Regularization in univariate case

이전 챕터까지의 모델들, Linear Regression, LDA, Logistic Regression, Seperating Hyperplane 등의 모델들은 독립변수들에 대한 선형성을 기반으로 모델이 구성되었었다. 하지만 대부분의 경우 \(f(X)\)는 \(X\)에 대해 선형적이지도, 가법적이지도 않다. 하지만 \(f(X)\)를 선형적인 모델로 표현한다면, 우리가 모델을 해석하는 데에 있어서 많은 이점이 있다. 따라서 이번 챕터에서는 basis function \(h\)을 이용하여 \(X\)에 대해 선형성을 띄지 않는 모델에 대해서도 선형적인 표현이 가능한 방법들을 알아볼 것이다.

Intro

\(X\)에 대한 \(m\)번째 basis function을 \(h_m : \mathbb{R}^p \rightarrow \mathbb{R}\)라고 하자. (\(m=1,...,M\)). 그렇다면 다음과 같은 모델을 \(X\)에 대한 linear basis expansion이라고 부른다.

\[f(X) = \beta_1h_1(X) + ... + \beta_Mh_M(X)\]

basis function \(h\)을 정의하는데는 여러가지 함수를 사용할 수 있겠지만, 일단 이번 포스팅에서는 piecewise-polynomial과 splines인 모델들에 대해서만 알아볼 것이다. 또한 제목에서 언급한 바와 같이 \(p=1\)인 즉, \(X\)와 \(y\)의 univariate한 경우에 대해서 먼저 다뤄볼 것이다.

piecewise polynomials and splines

먼저, piecewise polynomial이란 말 그대로 구간을 분리하여, 각 구간마다의 다항식을 세우는 방법이다. knot라고 불리는 기준점 \(\xi_1,...,\xi_K\)를 잡아 \((-\infty, \xi_1], [\xi_1,\xi_2], ... ,[\xi_{K-1}, \xi_{K}], [\xi_K, +\infty)\)로 각각의 구간을 나눈다. 이후 \(f(X)\)가 다항식의 차수가 1인, 즉 piecewise linear가 되도록 만들고 싶다면 다음과 같은 기저함수들을 고려해볼 수 있을 것이다.

\[h_1(X) = 1, h_2(X) = X, h_{2+k}(X) = (X-\xi_k)_+ \ (k=1,...,K) \text{ where } x_+ = \text{max}(0,x)\]

 

 

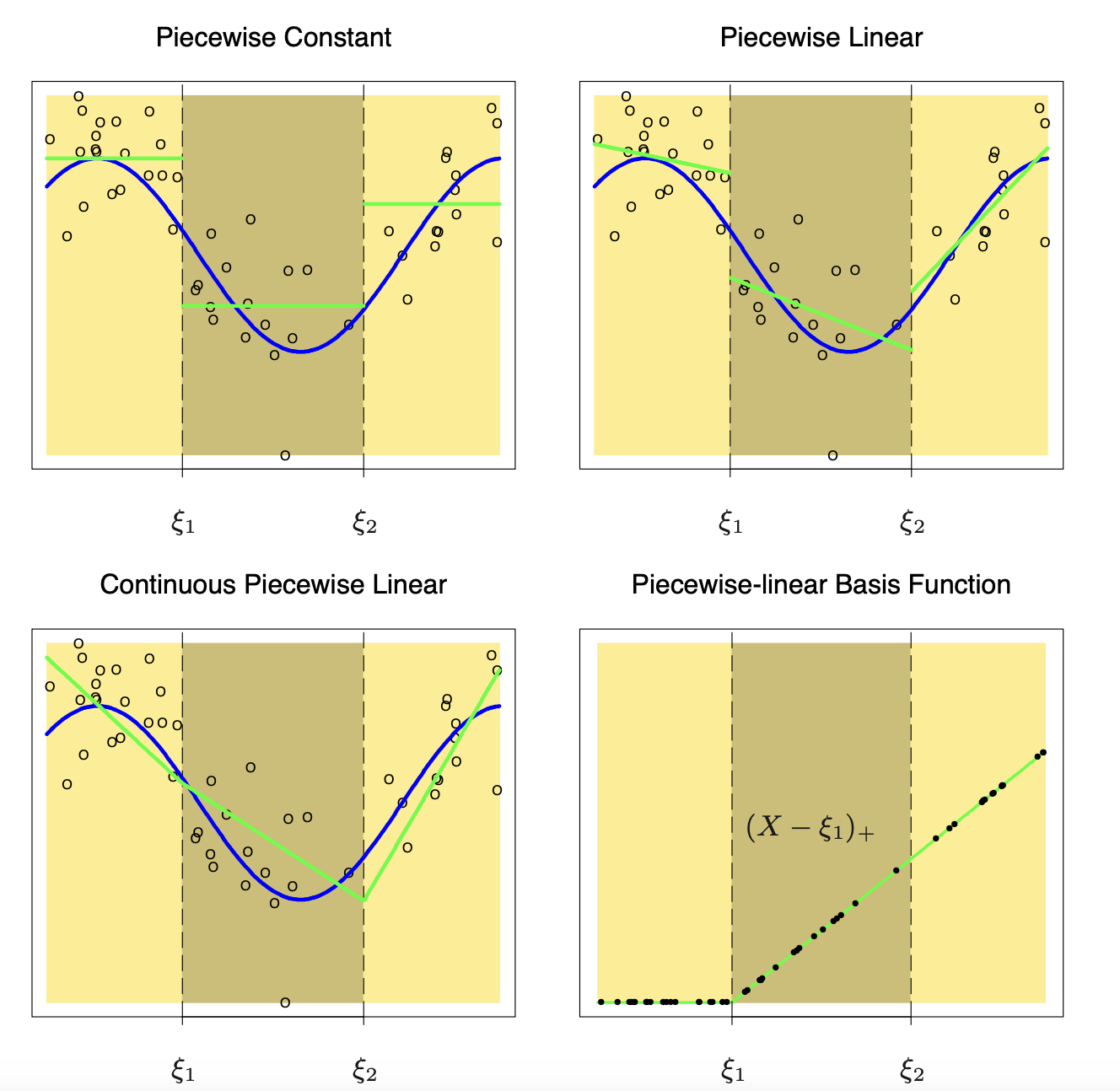
위 그림을 보면 알겠지만, 단순히 각 구간마다 M차 다항식을 더하는 것은 우리가 원하는 피팅이 아님을 알 수 있다. 이상적인 \(f(X)\)는 각 knot에서 연속이기를 원하고, 또한 부드러운 곡선모양을 그리는, 즉 spline 곡선일 것이다. 이러한 특징을 만족하는 M차 Spline 곡선 (a spline of \(f\) of degree M with knots at \(\xi_1 < ... < \xi_K\)) 을 수식으로 나타내면 다음과 같다.

• \(f\)는 각 구간 \((-\infty, \xi_1], [\xi_1,\xi_2],...,[\xi_K,\infty)\)에서 \(M\)차 다항식이다.
• \(l=0,...,M-1\)에 대해 \(f^{(l)}(x)\)은 \(\xi_1, ..., \xi_K\) 에서 연속이다.

즉 파라미터의 개수는 (구간의 수) x (다항식의 차수) - (연속성 제약조건)으로, \((K+1) \times (M+1) - M \times K = M + K + 1\)이다.

 

 

Regression Splines

위의 Spline 곡선의 조건을 만족하는 basis funciton \(h\)는 truncated power bases라고 불리는 다음과 같은 함수를 생각해볼 수 있다.

• \[h_j(X) = X^{j-1}, \ j=1,...,M+1\]
• \[h_{j+M+1}(X) = (X-\xi_{j})^M_+, \ j=1,...,K\]

truncates power basis를 이용한 \(f(X)\)가 spline의 정의를 만족하는지는 첫번째 조건은 바로 알 수 있고, 두번째 조건은 \(f(X) = \sum_{j=1}^{M+K+1}\beta_j h_j(X) = \sum_{j=0}^M \beta_jX^j + \sum_{k=1}^K (X-\xi_{k})^M_+\)의 좌미분계수와 우미분계수부터 (\(M-2\))번 미분했을 때 까지의 좌미분계수와 우미분계수가 같은지를 확인하면 충분할 것이다. 파라미터의 개수도 (\(M+K+1\))로 동일하다.

여기서 우리가 정해야 할 파라미터는 다항식의 차수 \(M\)과 knot의 개수와 위치, 총 3개의 파라미터이고 이에 따라 \(M+K+1\)개의 파라미터, 또는 자유도를 갖는다. 일반적으로 Splines의 차수는 \(M=0,1,3\)을 자주 사용하고 knot의 위치는 uniform quantile을 이용하여 정한다. 또한 위의 spline의 정의를 만족하는 다른 basis function을 정의할 수 있을 것이다. 이러한 \(f(X)\)가 spline이 되는 expansion방법을 Regression splines이라고 한다.

 

Natural Splines

하지만 이러한 보간법은 우리가 기준으로 삼은 knot의 양 끝 지점인 \((-\infty, \xi_1], [\xi_K, +\infty)\) 즉, boundary에서 원래 데이터와 맞지 않을 경향이 높을 것이다. 또한 이는 splines의 경우 문제가 더 심해진다. 따라서 양 끝 구간에서 더 느슨한 모양을 갖도록 다음과 같은 제약조건을 수정해준다.

• \(f\)는 각 구간 \([\xi_1,\xi_2],...,[\xi_K-1,\xi_K)\)에서 \(M\)차 다항식이다.
• \(f\)는 각 구간 \((-\infty, \xi_1], [\xi_K, +\infty)\)에서 \(\frac{M-1}{2}\)차 다항식이다.
• \(l=0,...,M=1\)에 대해 \(f^{(l)}(x)\)은 \(\xi_1, ..., \xi_K\) 에서 연속이다.

즉, 파라미터의 개수는 \((M+1)\times(K-1) + ((M-1)/2+1)\times 2 - M\times K = K\)이다.

자주 사용되는 \(M=3\)인 경우, truncated power basis를 이용하여 위의 수정된 제약조건을 만족하도록 함수를 조금 변형하면 다음과 같은 basis fucntion을 얻을 수 있다.

\[N_1(X)=1, \ N_2(X)=X, N_{k+2}(X) = d_k(X) - d_{K-1}(X), \\ \text{ where } d_k(X) = \frac{(X-\xi_k)^3_+ - (X-\xi_K)^3_+}{\xi_K-\xi_k}\]

이는 truncated power basis에서 boundary의 차수는 1임을 이용하여 \(N_1,N_2\)를 유도할 수 있고, 나머지는 위의 식을 넣어서 truncated power basis와 비교하면 같음을 알 수 있다.

Python code

이를 파이썬 코드로 구현하면 다음과 같다. 먼저 \(d_k(X)\)는 다음과 같이 정의한 \(dk\)를 이용하여 \(dk(X,k) - dk(X,K-1)\)로 나타낼 수 있다.

def dk(X,k,k_last):
    return (X-k).clip(0) **3 / (k_last - k)

 

따라서 \(N_{k+2}(X) = dk(X,k) - dk(X,K-1)\)로 나타낼 수 있다. 이를 이용하여 basis expansion를 다음과 같이 작성할 수 있다.

import numpy as np

def expand_natural_cubic_1D(X,ks):
    basis_splines = [np.ones(shape=(X.shape[0],1)), X]
    dki_last = dk(X,ks[-2],ks[-1])
    for knot in ks[:-2]:
        dki = dk(X,knot,ks[-1])
        basis_splines.append(dki - dki_last)

    return np.hstack(basis_splines)

 

Smoothing Splines

Smoothing splines는 Regression Splines에서 우리가 임의로 knot의 위치와 개수를 설정해야 하는 문제를 해결하기 위해 고안된 방법이다. 먼저 다음과 같은 문제를 생각해보자.

\[RSS(f,\lambda) = \sum_{i=1}^N \left \{ y_i - f(x_i) \right \}^2 + \lambda \int \{ f^{''}(t) \}^2dt \text{ where } \lambda >0 \text{ is fixed smoothing paramter}\]

즉, SSE와 두번째 항의 추가적인 패널티 항을 부과하는 문제이다. Ridge와 상당히 유사해보이는데, Ridge의 패널티항은 \(\|\beta\|^2_2\)으로 real vector space의 L2 norm이였다. 위의 식의 경우에서는 이계도 함수인 \(f^{''}\)의 크기를 줄여서 함수의 모양이 점점더 스무스해지도록 패널티를 가하는 것인데 함수의 크기를 마찬가지로 function space의 L2 norm인 \(\int \{ f^{''}(t) \}^2dt\)를 통해 정의해준 것이다. 이계도 함수는 함수의 곡률을 나타내주는 값이다. 그렇다면 곡률이 크다는 것은 함수의 굴곡이 상당히 크다는 것이다. 일반적으로, 굴곡이 크다면 함수의 모양이 구불구불하기에 오버피팅을 의심해 볼 수 있고, 반대로 너무 작다면 제대로 피팅이 안된 언더피팅임을 의심해볼 수 있을 것이다.

• \(\lambda = 0\): 곡률의 제약이 없다. 즉, 단순히 \(x_1,...,x_n\)들을 이어주는 곡률이 큰 매우 구불구불한 형태의 함수일 것이다.
• \(\lambda = \infty\): 곡률이 0이 되는, 즉 선형의 least square estimator가 될 것이다.

또한 위 문제와 Ridge와의 차이점은 Ridge의 경우 해당 criterion을 만족하는 real vector \(\beta\)를 찾는 것이지만, 위 문제는 실수가 아닌 함수 \(f(x)\)를 찾는 것이다. 더 자세히 말하면, 위의 패널티 항이 정의될 수 있는 무한차원 함수공간, Sobolev space \(W^{2,m}\) 이다.

왜 갑자기 함수의 곡률 즉, 이계도함수의 L2 norm의 제약 조건을 가하는 최적화 문제가 나왔나면, 무려 해당 문제는 유일해가 존재하며, 가능한 함수집함이 무한차원이였지만, 유한차원의 해인, knot가 \(x_1,...,x_n\) 즉 training data인, natural cubic spline esitmator이기 때문이다. 즉 다음과 같은 해가 도출된다.

\[f(x) = N_1(x)\theta_1 + ... + N_N(x)\theta_N\]

(증명)

먼저, 임의의 함수 \(f_0\)에 대하여, \(f_0(x_i) (i=1,...,n)\)을 knot로 잡는 natural cubic spline를 가정한다면 첫번째 항인 SSE가 같도록 하는 natural cubic spline을 잡을 수 있다. 따라서 두번째 항에 대해서만 고려를 하면 된다. 즉 문제를 다음과 같이 설정해보자.

임의의 구간 \([a,b]\) ( \(a<x_1<...<x_n<b\)인 \(a,b\)) 에서 미분가능하며 \((x_1, f_0(x_1)) , ..., (x_n, f_0(x_n))\)을 지나는 임의의 함수 \(\tilde{g}\) 와 마찬가지로, \((x_1, f_0(x_1)) , ..., (x_n, f_0(x_n))\)를 knot로 하는 natural cubic spline estimator를 \(g\) 라고 하자. 이 때의 모든 \(\tilde{g}\) 에 대하여, \(\int_a^b \tilde{g}^{''}(t)^2 dt \geq \int_a^b g^{''}(t)^2 dt\)임을 보이면 충분하다.

먼저 \(h(x) = \tilde{g}(x) - g(x)\)라고 정의하자. 가정에 의해, \(h(x_i) = 0 \ (i=1,...,n)\)이다. 따라서,

\[\begin{align*} \int_a^b g^{''}(t)h^{''}(t)dt &= \left[g^{'}(t)h^{'}(t)\right]^{t=b}_{t=a} - \int_a^bg^{'''}(t)h^{'}(t)dt \\ &= \left[g^{'}(b)h^{'}(b) - g^{'}(a)h^{'}(a) \right] - \left\{ \int_{a}^{x_1}g^{'''}(t)h^{'}(t)dt + \int_{x_1}^{x_n}g^{'''}(t)h^{'}(t)dt + \int_{x_n}^{b}g^{'''}(t)h^{'}(t)dt \right\} \\ &= - \int_{x_1}^{x_n}g^{'''}(t)h^{'}(t)dt \ (\because g \text{ is linear at boundary}) \\ &= -\sum_{j=1}^{N-1} \int_{x_j}^{x_j+1} g^{'''}(t)h^{'}(t)dt \\ &= -\sum_{j=1}^{N-1}c_j\left\{ h(x_{j+1}) - h(x_j)) \right\} \ (\because g^{'''} \text{ is constant on each interval}) \\ &= 0 \ (\because h(x_i) = 0 \text{ for } i=1,...,n) \end{align*}\]

즉, \(\int_a^b \tilde{g}^{''}(t)^2 dt = \int_a^b \tilde{g}^{''}(t)g^{''}(t) dt\)이다. 이를, \(h^{''}(t)^2\)에 대입하면 다음과 같은 부등식이 성립한다.

\[0 \leq \int_a^b h^{''}(t)^2 dt = \int_a^b g^{''}(t)^2dt - \int_a^b \tilde{g}^{''}(t)^2dt\]

따라서 \(\int_a^b \tilde{g}^{''}(t)^2 dt \geq \int_a^b g^{''}(t)^2 dt\)가 성립하고, 등식은 \(h(x)\)가 상수인 경우에 성립하지만, 가정에의해 \(h(x_1) = ... = h(x_n) = 0\)이여야 하므로 \(h(x) =0\) 즉, \(\tilde{g} = g\) 인 경우에만 성립한다. 즉 유일성이 보장된다.

 

이제, \(f(x) = \sum_{j=1}^N N_j(x)\theta_j\) 를 RSS에 대입해보자. 이를 행렬표현으로 나타내기 위해 다음과 같은 행렬 \(N, \Omega_N\)을 정의해보자. (주의. \(x_1,...,x_n\)에 중복된 원소가 존재한다면, 위 행렬들은 \(N \times N\) 행렬이 아닐 수 있다. 하지만 편의를 위해 모두 고유한 값을 갖는다고 가정하자.)

\[\left\{ N\right\}_{i,j} = N_j(x_i), \left\{ \Omega_N \right\}_{i,j} = \int N_i^{''}(t)N_j^{''}(t)dt\]

RSS는 다음과 같이 나타낼 수 있다.

\[RSS(\theta,\lambda) = (\mathbf{y} - N\theta)^T(\mathbf{y} - N\theta) + \lambda \theta^T\Omega_N\theta\]

즉 위를 최소화 하는 \(\hat{\theta} = (N^TN + \lambda \Omega_N)^{-1}N^T\mathbf{y}\)를 얻을 수 있다. \(\lambda\)의 경우에서는 마찬가지로, cross validation을 통해 최적의 파라미터를 찾을 수 있을 것이다.

Pyhton code

natural spline에서 basis function \(N\)을 구현하였으므로, \(\Omega_N\)을 구현하면 충분하다. 즉 각 원소마다 다음을 계산해야 한다.

\[\begin{align*}\{\Omega_N \}_{ij} &= \int N_i^{''}(t)N_j^{''}(t)dt \\ &= \int_{\xi_j}^{\xi_K} (dk^{''}(t,i) - dk^{''}(t,K-1))(dk^{''}(t,j) - dk^{''}(t,K-1))dt \\ &= \int_{\xi_j}^{\xi_{K-1}}dk^{''}(t,i)dk^{''}(t,j)dt + \int_{\xi_{K-1}}^{\xi_K} (dk^{''}(t,i) - dk^{''}(t,K-1))(dk^{''}(t,j) - dk^{''}(t,K-1))dt \end{align*}\]

즉 위에서 정의한 함수 dk에 대한 이계도 미분함수의 곱에 대한 적분을 위 구간과 같이 나눠서 계산을 해야한다. 이를 심파이를 이용하여 수식으로 나타내면 아래와 같다.

\[\frac{-18\xi_i\xi_j^2 + 24\xi_i \xi_j\xi_{K-1} + 12 \xi_i \xi_j\xi_{K} - 6\xi_i \xi_{K-1}^2 - 12\xi_i \xi_{K-1}\xi_{K} + 6 \xi_j^3 - 6 \xi_j\xi_{K-1}^2 - 12 \xi_j \xi_{K-1}\xi_{K} + 12\xi_{K-1}^2\xi_{K}}{\xi_i \xi_j - \xi_i \xi_K - \xi_j\xi_{K} + \xi_K^2}\]

이를 구현한 코드는 다음과 같다. \(N_1(X) = 1, N_2(X) = X\)이기에 이계도함수가 0이므로, 첫번째와 두번째의 행과 열은 모두 0이기에 따로 계산하지 않는다.

import numpy as np

Omega = np.zeros((len(knots), len(knots)))

def calc_integral(i, j, p, l):
        return (-18*i*j*j + 12*i*j*l + 24*i*j*p - 12*i*l*p - 6*i*p*p +
                6*j*j*j - 12*j*l*p - 6*j*p*p + 12*l*p*p) / (i*j - i*l - j*l + l*l)

for i in range(2, len(knots)):
    for j in range(2, len(knots)):
        Omega[i,j] = Omega[j,i] = calc_integral(knots[i-2],knots[j-2],knots[-2],knots[-1])

따라서 \(\hat{\theta}\)은 다음과 같이 구할 수 있다.

import numpy as np

theta_hat = np.linalg.inv(N.T@N + lambda_ * Omega) @ N.T @ y

 

Degrees of freedom

Smooting splines도 ridge에서와 마찬가지로 자유도를 정의해야 할 것이다. \(\lambda\)가 주어졌다 가정하고, 학습데이터에 대한 fitted values를 \(\hat{\mathbf{f}}_{\lambda}\)라고 하자.

\[\hat{\mathbf{f}}_{\lambda} = N(N^TN + \lambda \Omega_N)^{-1} N^T \mathbf{y} = S_{\lambda}\mathbf{y}\]

즉, fitted values는 \(\mathbf{y}\)의 선형결합으로 linear operator \(S_{\lambda}\)를 이용해 나타낼 수 있다. 이 때의 \(S_{\lambda}\)를 smoother matrix라고 한다.

이를 \(M\)개의 knot를 갖는 cubic splines에 대한 선형회귀의 경우와 비교해보자. 학습데이터를 이 spline에 의해 expansion된 데이터를 \(B_{\xi}\)라고 하자. 그렇다면 fitted values \(\hat{\mathbf{f}}_{\xi}\)는 다음과 같다.

\[\hat{\mathbf{f}}_{\xi} = B_{\xi}(B_{\xi}^TB_{\xi})^{-1}B_{\xi}^T\mathbf{y}= H_{\xi}\mathbf{y}\]

즉 basis function에 의해 expansion이 일어난 데이터에 대한 hat matrix \(H_{\xi}\)가 linear operator이다. 각각의 linear operator \(S_{\lambda}, H_{\xi}\)를 비교해보자.

먼저 두 행렬은 모두 symmetric positive semi-definite이다. 둘다 symmetric임은 바로 알 수 있고, positive semi-definite에 대해서는, \(H_{\xi}\)의 경우는 이미 알고 있고, \(S_{\lambda}\)의 경우, \(\Omega_N\)에 대해서만 확인하면 되는데, \(\theta^T\Omega_N \theta = \sum_i\sum_j \theta_i \int N_i^{''}(t)\int N_j^{''}(t)dt \theta_j = \int (\sum_i N_i^{''}(t)\theta_i)^2 dt \geq 0\)임을 알 수 있다.

\(H_{\xi} H_{\xi} = H_{\xi}\)로 idempotent이고, \(S_{\lambda}S_{\lambda} + A = S_{\lambda}\) (\(A\)는 positive semi-definite)로 shirinkage 효과가 있음을 짐작해볼 수 있다.

마지막으로, 파라미터인 basis function의 수는 rank(\(H_{\xi}\)) = \(M\)이고, rank(\(S_{\lambda}\)) = \(N\)이다. 또한 \(M = tr(H_{\xi})\)으로, 이는 파라미터의 수와 같다. 따라서 이와 유사하게, Smooting splines의 자유도, effective degrees of freedom을 \(\text{df}_{\lambda} = tr(S_{\lambda})\)로 정의한다.

 

Reinsch Form

위와 같은 방법으로 자유도를 정의하게 되면, Reinsch form을 통해 smootihg splines을 바라볼때의 다음과 같은 몇몇의 인사이트를 찾아볼 수 있다. 먼저 \(K = (N^T)^{-1}\Omega_N N^{-1}\)을 정의하면, \(S_{\lambda} = (I + \lambda K)^{-1}\)임을 알 수 있다. 또한 \(K\)도 마찬가지로 symmetric positive semi-definite임을 알 수 있다. 이를 Reinsch form이라고 한다. \(K\)를 penalty matrix라고도 하는데, \(\hat{\mathbf{f}}_{\lambda}\)가 다음과 같은 문제의 해가 되기 때문이다.

\[\underset{\mathbf{f}}{\text{argmin}} (\mathbf{y} - \mathbf{f})^T(\mathbf{y} - \mathbf{f}) + \lambda \mathbf{f}^TK\mathbf{f}\]

\(K\)의 고윳값 분해를 \(K = UDU^T\) (\(D = diag(d_1,...,d_n)\), U는 orthogonal matrix) 라고 하자. 그렇다면 \(S_{\lambda}\)를 다음과 같이 분해할 수 있다.

\[\begin{align*} S_{\lambda} &= (I + \lambda K)^{-1} = \left\{U(I + \lambda D)U^T\right\}^{-1} \\ &= U(I+\lambda D)U^{T} = \sum_{k=1}^N \rho_k(\lambda)u_ku_k^T \text{ where } \rho_k(\lambda) = \frac{1}{1+\lambda d_k} \end{align*}\]

즉, effective degrees of freedom은 \(tr(S_{\lambda}) = \sum_{k=1}^N \frac{1}{1+\lambda d_k}\)이다. 즉, \(\lambda\)에 대한 monotone 함수이기에 effective degrees of freedom과 \(\lambda\)는 일대일 대응관계를 갖는다. 따라서, 이를 자유도로 설정하여 다른 smooting 모델과의 비교를 해볼 수 있다.

흥미로운 점은 \(S_{\lambda}\)의 고유벡터가 되는 \(u_k\)는 원래 \(K\)의 고유벡터로 \(\lambda\)의 영향을 받지 않는다. 또한 \(\hat{\mathbf{f}}_{\lambda} = \sum_{k=1}^N u_k (\rho_k(\lambda)u_k^T\mathbf{y})\)로 스칼라 \((\rho_k(\lambda)u_k^T\mathbf{y})\)들을 통한 고유벡터 기저 \(u_k\)의 선형결합이다. 각 \(k\)번째 원소들은 \(\rho_k(\lambda)\)에 따라 즉, \(\lambda\)에 의해 다르게 영향을 받는 shrinkage가 일어났다. \(\hat{\mathbf{f}}_{\xi} = H_{\xi}\mathbf{y} = \sum_{k=1}^N h_iu_iu_i^T\mathbf{y}\)의 경우, 각 \(h_i\)는 0과 1로, 해당 원소가 결합에 관여하거나 아니거나 하는 selection방법과는 차이가 있다.

 

Equivalent kernel

임의의 test point \(x\)에 대하여 smooting spline estimator는

\[\hat{f}(x) = (N_1(x), ... , N_N(x)) ^T (N^TN + \lambda \Omega_N)^{-1}N^T\mathbf{y} = w(x)^T\mathbf{y}, \\ \text{ where } w(x) = ( w_1(x), ...., w_N(x))\]

라는 \(w\)에 대한 가중치를 강조하여 나타낼 수 있다. 각각의 \(w_i(x)\)들은 학습데이터 \(x_i\)들의 영향을 받으므로, 이를 나타내기 위해 \(w_i(x) = w(x,x_i)\)꼴로 표현해보자. 즉, \(\hat{f}(x) = w(x,x_1)y_1 + ... + w(x,x_n)y_N\)꼴로 나타낼 수 있다. 즉 \(w\)가 커널과 같은 형태이고 이것이 어떻게 작용하는지, 학습데이터에 대해서 생각해보자. 즉 \(\hat{\mathbf{f}}_{\lambda}\)를 고려해보면, \(S_{\lambda}\)의 \(i\)번째 행이 \((w(x_i,x_1), ..., w(x_i,x_N))\)임을 알 수 있다. \(S_{\lambda}\)의 원소들을 그래프로 나타내면 다음과 같다.

 

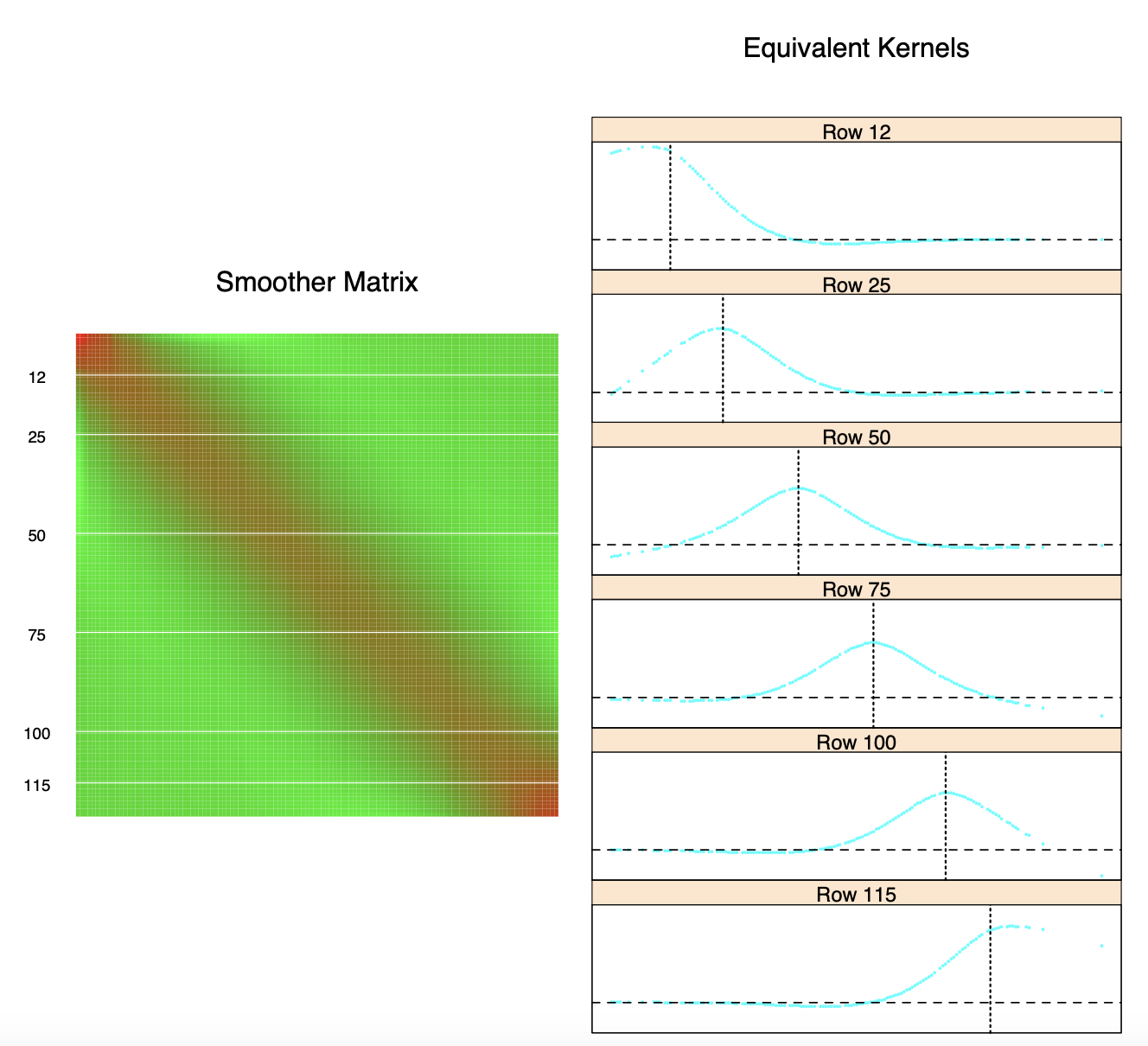
즉, 각 \(x_i\)마다의 커널의 모양이 같고 단지 평행이동이 일어났음을 알 수 있다. 때문에 이를 equivalent kernel이라고 한다. 사실 \(n\)이 충분히 크고, 특정 조건하에서 \(w\)는 다음과 같이 근사될 수 있다.

\[\begin{align*} w(x,z) &\approx \frac{1}{h(x)p(x)}K\left(\frac{x-z}{h(x}\right), \\ \text{where } &p(x) \text{ is distribution at } x, \\ &h(x)=(\frac{\lambda}{p(x)})^{\frac{1}{4}} \text{ is band-width which adapts to local distribution of } x \\ &K(x) = \frac{1}{2}\exp(-\frac{|t|}{\sqrt{2}})\sin(\frac{|t|}{\sqrt{2}} + \frac{\pi}{4}) \text{ which is known as Silverman kernel} \end{align*}\]

즉, smooting spline estimator는 asymptotic하게 kernel regression estimator와 동치임을 알 수 있다.

 

다음 포스팅에서는 다차원에서의 basis expansion과 RKHS에 대해서 다뤄볼 예정이다.