이전 포스팅에서 분류 문제는posterior를 최대화하는 클래스를 찾는 것임을 알 수 있었다. Linear Regression의 경우 조건부 기댓값을 추정하는데, 종속 변수를 indicator 변수로 변환하면 조건부 기댓값이 posterior가 된다는 것을 이용하여 예측을 진행하였다. LDA에서는 베이즈 정리를 활용하여 prior와 likelihood를 데이터로부터 추정해서 특정 확률분포를 posterior를 따름을 가정하였다. 이번 포스팅에서는 직접 posterior를 유도하는 Logistic regression과 바로 hyperplane를 추정하는 두가지 방법을 알아볼 것이다.
Logistic Regression
Logistic Regression은 각각의 \(K\)개의 클래스의 posterior를 다음과 같이 decision boundary가 linear하도록 모델링을 진행한다.
\[\log{\frac{Pr(G=k|X=x)}{Pr(G=K|X=x)}} = \beta_{k0} + \beta_k^Tx \ \text{for} \ k = 1,...,K-1\]즉, 각각의 posterior는 다음과 같다.
\[\begin{align*} Pr(G=k|X=x) &= \frac{\exp(\beta_{k0}+\beta_k^Tx)}{1+\sum_{l=1}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)} \ \text{for} \ k = 1,...,K-1 \\ Pr(G=K|X=x) &= \frac{1}{1+\sum_{l=1}^{K-1}\exp(\beta_{l0}+\beta_l^Tx)} \end{align*}\]posterior의 파라미터를 더 알아보기 쉽게 다음과 같이 표기하겠다.
\[\theta = \{ \beta_{10}, \beta_1^T,...,\beta_{(K-1)0}, \beta_{K-1}^T \}, \ Pr(G=k|X=x) = p_k(x;\theta)\]Fitting Logistic Regression
Logistic Regression은 일반적으로
\(G|X\)
의 likelihood를 최대화 하는 방식으로 fitting을 진행한다. 위에서
\(Pr(G|X)\)
를 가정하였으므로, 다항분포를 사용하는 것이 적절할 것이다. 수식의 간결성을 위해 앞으로의 논의는 이진분류로만 한정하여 나가보자. 즉, log-likelihood는 다음과 같이 쓸 수 있다.
이제 뉴턴-랩슨법을 사용하여 이를 풀어보자. 먼저 \(\beta\)에 대한 미분을 진행하면 다음과 같다.
\[\frac{\partial l(\beta)}{\partial \beta} = \sum_{i=1}^N x_i(y_i - p(x_i;\beta)) = \mathbf{X}^T(\mathbf{y} - \mathbf{p}) \ \text{where} \ \mathbf{p} \ \text{the vector of} \ p(x_i;\beta^{old})\] \[\frac{\partial^2 l(\beta)}{\partial \beta \partial \beta^T} = -\sum_{i=1}^Nx_ix_i^Tp(x_i;\beta)(1-p(x_i;\beta)) = -\mathbf{X}^T\mathbf{W}\mathbf{X} \ \text{where} \ \mathbf{W} \text{ a diagonal matrix with} \\ \mathbf{W}_{ii} = p(x_i;\beta^{old})(1-p(x_i;\beta^{old})).\]즉, 다음과 같이 업데이트를 진행한다.
\[\begin{align*} \beta^{new} &= \beta^{old} + (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T(\mathbf{y}-\mathbf{p}) \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}(\mathbf{X}\beta^{old} +\mathbf{W}^{-1}(\mathbf{y} -\mathbf{p})) \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{z} \text{ where } \mathbf{z}=\mathbf{X}\beta^{old} +\mathbf{W}^{-1}(\mathbf{y} -\mathbf{p}) \end{align*}\]매 업데이트마다, \(\mathbf{z}\)에 대하여 weighted least squared 문제를 푸는 것과 같다. 여기서, \(\mathbf{z}\)는 adjusted respones라고도 불린다. 매 스텝마다 \(\mathbf{p}\)가 바뀌기에, 마찬가지로 \(\mathbf{W}, \mathbf{z}\)도 반복적으로 업데이트가 진행되기에 이를 iteratively reweighted least squares(IRLS)라고 불리기도 한다. 즉, 매 스탭마다 다음과 같은 문제를 푸는 것이다.
\[\beta^{new} \leftarrow \underset{\beta}{\mathrm{argmin}} (\mathbf{z}-\mathbf{X}\beta)^T\mathbf{W}(\mathbf{z}-\mathbf{X}\beta)\]따라서 least squares problem과 같이 초기 \(\beta\)값은 0으로 설정하는 것이 합리적으로 보인다. 또한 log-likehood가 concave하기에 convergence가 보장이 된다. 하지만 overshooting이 일어날 수 있기에, 해당 경우에는 스텝 사이즈를 줄이는 것이 합리적일 것이다.
Quadratic Approximations and Inference
\(\hat{\beta}\)를 likelihood를 최대화는 방식으로 fitting을 진행하면, 위에서 보인 바와 같이 self-consistency 관계가 있다. 다시말해서, 매 iteration마다 \(\hat{\beta}\)는 adjusted response \(z_i\)에 대하여 가중치 \(w_i = \hat{p}_i (1 - \hat{p}_i)\)의 weighted least squres fit을 통해 업데이트를 진행하는데, 두 변수 모두 \(\hat{\beta}\)에 의존하는 \(\hat{p}_i\)의 영향을 받고 있다. 이처럼 반복적인 계산이 필요해 비용이 드는 알고리즘이지만, least squres와의 다음과 같은 추가적인 연관성들이 있다.
- Deviance의 이차 근사값이 카이제곱 통계량과 같다.
Deviance는 least squres에서의 RSS를 MLE에서 일반화한 통계량으로 다음과 같다.
\[D = -2l(\beta) + 2l(\text{perfect fitting})\]아래의 그림처럼 perfect fitting의 likelihood가 가장 높으므로 deviance는 항상 음이 아니 값을 갖고, 부정확할 수록 더 큰 값을 가지게 될 것이다.

logistic regression의 경우 perfect fitting의 likelihood는 기존 likelihood 함수의 \(p\)값을 \(y\)값으로 대체한 값이다. 이를 테일러 근사법을 이용하여 2차식까지 근사하면 다음과 같이 카이제곱 통계량임을 보일 수 있다.
\[\begin{align*} D &= -2\sum_{i=1}^N \{ y_i \log{\hat{p}_i} + (1-y_i) \log{(1-\hat{p}_i)}\} + 2\sum_{i=1}^N \{ y_i \log{y_i} + (1-y_i) \log{(1-y_i)}\} \\ &= 2\sum_{i=1}^N [y_i \log{\frac{y_i}{\hat{p}_i}} + (1-y_i) \log{\frac{1-y_i}{1-\hat{p}_i}}]\\ &\approx 2\sum_{i=1}^N[ (y_i-\hat{p}_i) + \frac{(y_i-\hat{p}_i)^2}{2\hat{p}_i} + \{(1-y_i)-(1-\hat{p}_i)\} + \frac{\{(1-y_i)-(1-\hat{p}_i)\}^2}{2(1-\hat{p}_i)}] \\ &= \sum_{i=1}^N\frac{(y_i-\hat{p}_i)^2}{\hat{p_i}} + \frac{y_i-\hat{p}_i}{1-\hat{p}_i} \\ &= \sum_{i=1}^N\frac{(y_i-\hat{p}_i)^2}{\hat{p_i}(1-\hat{p_i})} \end{align*}\]
-
Asymptotic likelihood theory에 의하면 correct model에 대해서 MLE는 constistent하다. 즉, \(\hat{\beta}\)는 \(\beta\)로 수렴한다.
즉 위에서 제시한 logistic regression 모델의 가정이 데이터와 들어맞다면, consistent한 estimator를 얻을 수 있다.
-
CLT에 의해 \(\hat{\beta}\)는 \(\mathcal{N}(\beta, (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1})\)로 수렴한다.
먼저, \(y_i \overset{\mathrm{iid}}{\sim} Bernoulli(p_i)\)를 따른다. 따라서 \(\mathbf{y}\)의 기댓값과 분산은 다음과 같다.
\[\mathbb{E}[\mathbf{y}] = \mathbf{p}, \ Var[\mathbf{y}] = \mathbf{W}\]이를 이용하여, \(\hat{\beta}\)의 기댓값과 분산을 구하면 다음과 같다.
\[\begin{align*} \mathbb{E}[\hat{\beta}] &= \mathbb{E}[(\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{z}] \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbb{E}[\mathbf{X}\beta +\mathbf{W}^{-1}(\mathbf{y} -\mathbf{p})] \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{X}\beta =\beta \\ \\ Var[\hat{\beta}] &= Var[(\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}\mathbf{z}] \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}Var[\mathbf{X}\beta +\mathbf{W}^{-1}(\mathbf{y} -\mathbf{p})]((\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W})^T \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W}(\mathbf{W}^{-1}\mathbf{W}{\mathbf{W}^{-1}}^T)((\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^T\mathbf{W})^T \\ &= (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1} \end{align*}\]즉 충분히 큰 \(N\)에 대하여 CLT에 의해 \(\hat{\beta} \sim \mathcal{N}(\beta, (\mathbf{X}^T\mathbf{W}\mathbf{X})^{-1})\)를 따른다.
- MLE를 기반으로 하는 Rao score test, Wald test을 이용하여 반복적인 계산을 피해 효율적인 구현이 가능하다.
OLS에서의 variable selction 방법을 Rao score test, Wald test를 통해 적용해볼 수 있다.
L1 Regularized Logistic Regression
Logistic regression에서도 linear model에서의 Lasso와 같이 L1 penalty를 부여하여 variable selection 및 shringkage를 얻을 수 있다.
\[\underset{\beta_0,\beta}{\mathrm{max}} \left[ \sum_{i=1}^N\{y_i(\beta_0 + \beta^Tx_i) - \log(1+\exp(\beta_0 + \beta^Tx))\} - \lambda\sum_{j=1}^p|\beta_p| \right]\]위 식은 concave하고, nonlinear programming방법을 통해 해를 구할 수 있다. 또한 위에서와 같이 뉴턴법을 이용하여 반복적인 방법으로 해를 구할 수 있다. 또한 non-zero coefficient에 대한 score equation은 다음과 같다.
\[\frac{\partial l}{\partial \beta_j} = \mathbf{x}_j^T(\mathbf{y} - \mathbf{p}) - \lambda \cdot \text{sign}(\beta_j) = 0, \ \mathbf{x}_j^T(\mathbf{y} - \mathbf{p}) = \lambda \cdot \text{sign}(\beta_j)\]Logistic regresison의 경우 coefficient profile이 linear가 아닌 piecewise smooth하므로, LAR 같은 Path algorithm을 사용할 수 없기에 이차 근사를 활용한 방법을 사용한다. 다음은 R패키지의 glmpath를 이용하여 path를 구한 것이다. active set의 variable들이 바뀌는 지점의 \(\lambda\)를 predictor-correct methods 방법을 사용하여 근사를 진행한다. 이를 통해 구한 path는 다음과 같이 거의 linear하다는 것을 알 수 있다.
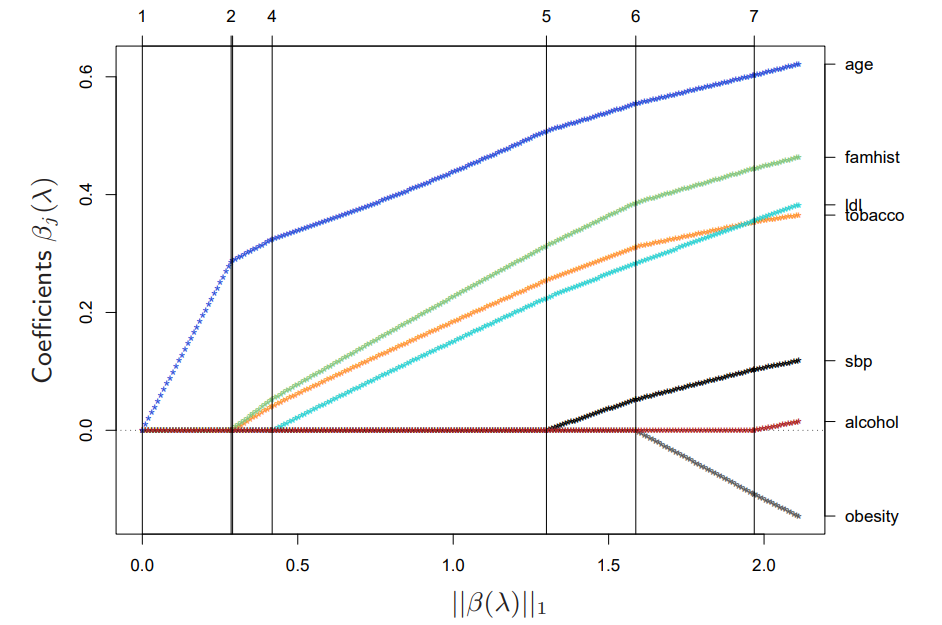
또한 각 \(\lambda\)에서의 coefficient의 업데이트는 coordinate descents methods를 통해 효율적으로 계산할 수 있다. 이에 대한 내용은 이후 18장에서 더 자세히 다룰 예정이다.
Optimal Seperating Hyperplanes
해당 알고리즘은 두개의 클래스를 분리하며, 각 클래스마다 가장 가까운 점들과의 거리를 최대화하는 초평면을 생성한다. 여기서 가장 가까운 점과 초평면사이의 거리를 마진(margin)이라고 한다. 이렇게 만들어진 초평면은 유일성을 보장하고, 학습 데이터에서 마진을 최대화한 초평면은 테스트 데이터에 대한 분류에서도 좋은 성능을 보인다. 이를 마진을 \(M\)으로 나타내어 수식으로 나타내면 다음과 같다.
\[\underset{\beta, \beta_0, \|\beta\|=1}{\text{max}} M \text{ subject to } y_i(x_i^T\beta + \beta_0) \geq M, \ i=1,...,N\]
Note. \(M\)의 제약조건이 위와 같은 이유는 다음과 같다.
\(\mathbb{R}^2\)에서 다음과 같은 녹색 직선인 초평면 \(L = \{ x: f(x) = \beta_0 + \beta^Tx = 0 \}\) 가정해보자.
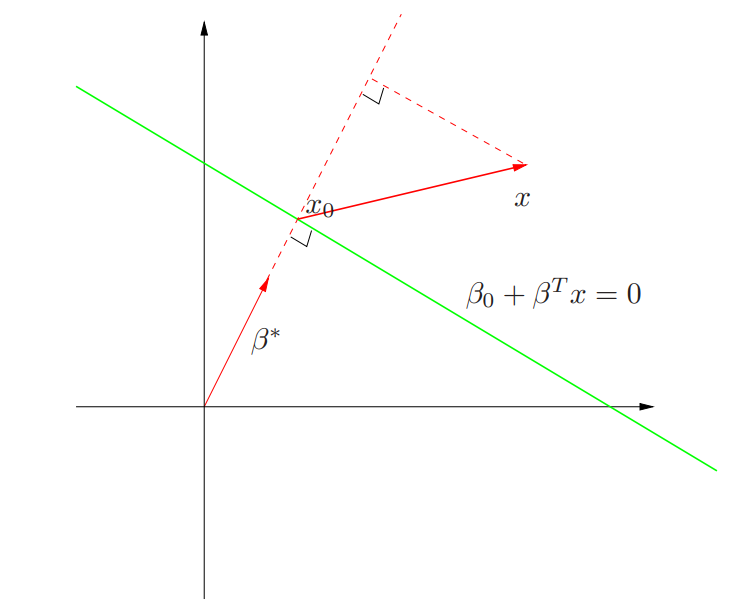
초평면 \(L\) 위에 놓여있는 임의의 두 점 \(x_1, x_2\)에 대하여, \(\beta^T(x_1 - x_2) = 0\)이다. 즉, \(\beta^* = \beta / \|\beta\|\) 는 \(L\)의 단위 법선 벡터(unit normal vector)이다. 따라서 임의의 \(x\)와 \(L\)상의 \(x_0\)에 대해 다음이 성립한다.
\[{\beta^*}^T(x-x_0) = \frac{1}{\|\beta\|}(\beta^Tx + \beta_0) \ (\because \beta^Tx_0 = -\beta_0)\]즉 임의의 \(x\)와 초평면 \(L\)사이의 거리는 \(\beta^Tx + \beta_0\)에 비례한다. 또한 제약조건의 좌변에서 추가적으로 \(y_i\)를 곱하여 부호를 맞춰준다. 마지막으로, \(\|\beta\|=1\) 의 제약조건은 해의 유일성을 위하여 추가한 것이다.
이를 \(\beta\)의크기에 대한 제약 지우기 위하여 다시 쓰면 다음과 같다.
\[\underset{\beta, \beta_0}{\text{max}} \ M \text{ subject to } y_i(x_i^T\beta + \beta_0) \geq M \|\beta\|, \ i=1,...,N\]또한, \(M\)을 최대화 하는 것은 \(\beta\)의 유일성에 대한 제약 조건을 \(\beta\)의 크기를 \(1/M\)이 되도록 잡는 것으로 수정하면, \(\beta\)의 크기를 최소화하는 것과 같다. 즉 다음과 같다.
\[\underset{\beta, \beta_0}{\text{min}} \ \frac{1}{2}\|\beta\|^2 \text{ subject to } y_i(x_i^T\beta + \beta_0) \geq 1, \ i=1,...,N\]따라서 마진의 크기는 \(\beta\)의 크기의 역수와 같다. 즉, 파라미터 \(\beta, \beta_0\)를 이용하여 적절한 마진의 크기를 정하는 것이다. 이는 convex optimization 문제로 쌍대 문제로 변환하여 풀 수 있다.
Lagrange Duality
먼저, 다음과 같은 제약조건이 있는 문제를 푼다고 가정하자. (convexity와 같은 \(f,g_i, h_i\)에 대한 가정은 따로 없다.)
\[\begin{align*} p^* =\underset{x}{\text{min}} \ f(x) \\ \text{subject to } &g_i(x) \leq 0, \ i=1,..,m \\ &h_j(x) = 0,j=1,...,p \end{align*}\]즉 라그랑지안을 통해 다음을 최소화하는 것과 같다.
\[\mathcal{L}(x, \alpha, \beta) = f(x) + \sum_{i} \alpha_ig_i(x) + \sum_{j}\beta_j \text{ where } \alpha \geq 0 \text{ for all } i\]이에 대하여 다음과 같은 쌍대 함수(dual function)을 정의해보자.
\[\mathcal{D}(\alpha,\beta) = \underset{x}{\text{min}} \ \mathcal{L}(x,\alpha,\beta)\]따라서, \(\mathcal{D}(\alpha,\beta)\)는 항상 \(p^*\)보다 작거나 같음을 알 수 있다. 이제 다음과 같은 쌍대문제(dual prolem)을 생각해보자.
\[d^* =\underset{x}{\text{min}} \ \mathcal{D}(\alpha,\beta) \text{ subject to } \alpha \geq 0\]마찬가지로, \(d^* \leq p^*\)이다. 이를 weak duality라고 한다. 또한 \(p^* - d^*\)를 duality gap, duality gap이 \(0\)인 경우를 strong duality라고 한다.
KKT optimality condition
만약, \(x^*, \alpha^*, \beta^*\)가 다음의 KKT 조건을 만족하면, 이는 string duality을 만족하는 primal과 dual 문제의 해이다.
- (Stationarity) \(0 \in \partial \left( f(x) + \sum_i \alpha_i g_i(x) + \sum_j \beta_j h_j(x) \right)\)
- (Complementary Slackness) \(\alpha_i g_i(x) = 0 \text{ for all } i\)
- (Primal Feasibility) \(g_i(x) \leq 0, \ h_j(x) = 0 \text{ for all } i,j\)
- (Dual Feasibility) \(\alpha_i \geq 0 \text{ for all } i\)
증명과정은 다음과 같다.
(Sufficiency)
KKT조건을 만족하는 \(x^*, \alpha^*, \beta^*\)가 존재하면, 이는 primal and dual optimal임을 보이면 된다.
\[\begin{align*} \mathcal{D}(\alpha^*, \beta^*) &=f(x^*) + \sum_i \alpha^*g_i(x^*) + \sum_j \beta_j^*h_j(x^*) (\because \text{by 1}) \\ &= f(x^*) \ (\because \text{by 2,3}) \end{align*}\](Necessity)
반대로 \(x^*, \alpha^*, \beta^*\)가 zero duality gap이면, KKT조건을 만족함을 보이면 된다.
\[\begin{align*} f(x^*) &= D(\alpha^*, \beta^*) \ (\because \text{by zero duality gap}) \\ &= \underset{x}{\text{min}} \ f(x) + \sum_i \alpha^*g_i(x^*) + \sum_j \beta_j^*h_j(x^*) \\ &\leq f(x^*) + \sum_i \alpha^*g_i(x^*) + \sum_j \beta_j^*h_j(x^*) \\ &\leq f(x^*) \ (\because \text{by initial assumption}) \end{align*}\]또, 3번째와 마지막 수식에서는 등식이 성립해야하기에 각각 조건 1과 2,3을 만족한다.
Fitting Optimal Seperating Hyperplanes
이제 Optimal Seperating Hyperplanes에서의 원문제를 다음과 같이 라그랑지안과 듀얼로변환해보자.
\[L_p = \frac{1}{2} \| \beta \|^2 - \sum_{i=1}^N \alpha_i \left[ y_i(x_i^T\beta + \beta_0) - 1 \right] \text{ subject to } \alpha\geq0\]각각 \(\beta_0, \beta\)에 대하여 미분하여 0이되는 지점을 대입하면 듀얼 문제를 구하면 다음과 같다.
\[\beta = \sum_{i=1}^N\alpha_iy_ix_i, \ \sum_{i=1}^N\alpha_iy_i = 0\] \[L_D = \sum_{i=1}^N \alpha_i - \frac{1}{2}\sum_{i=1}^N\sum_{k=1}^N\alpha_i\alpha_ky_iy_kx_i^Tx_k \ \text{subject to} \ \alpha_i \geq 0\]즉, KKT조건을 만족하려면 추가적으로 Complementary slackness를 만족해야 한다. 즉,
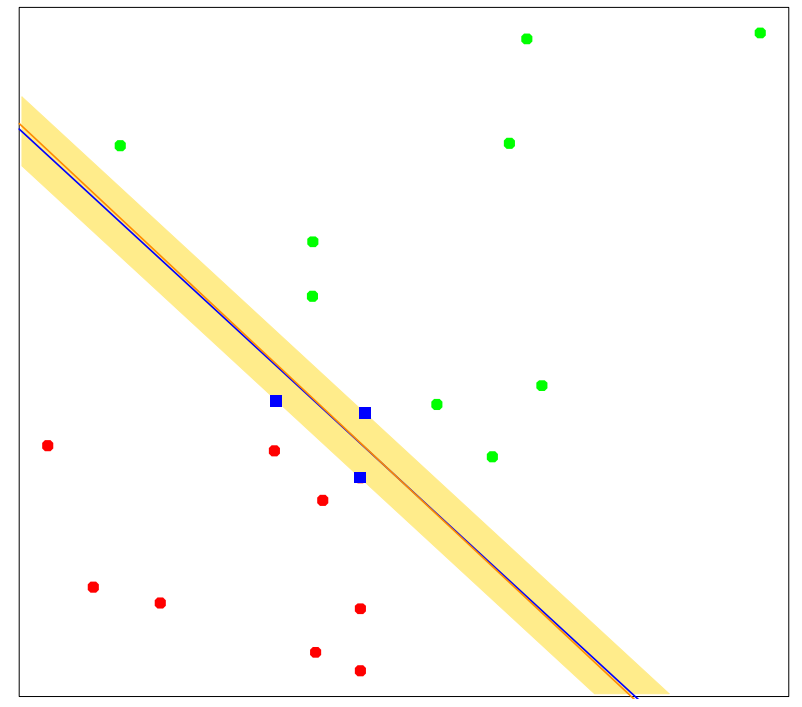
\[\alpha_i [y_i(x_i^T\beta + \beta_0)-1] = 0 \ \text{for all} \ i.\]이다. 따라서 만약 \(\alpha_i\)가 0보다 크다면, \(y_i(x_i^T\beta + \beta_0) = 1\)로 경계선(slab) 상에 존재하는 것이다. 반대로 경계선 상이 아닌 \(y_i(x_i^T\beta + \beta_0) = 1\)일 경우에는, \(\alpha_i = 0\)이다. 이러한 \(\alpha_i > 0\)인 경계선 상의 \(x_i\)들을 support vector라고 부르고, 이들의 선형결합으로 인해 \(\beta\)가 정의된다. 즉, 이러한 support vector들의 인덱스 집합 \(\mathcal{S}\)에 대하여 다음과 같다.
\[\beta = \sum_{i\in\mathcal{S}}\alpha_iy_ix_i\]아래는 간단한 데이터셋을 통해 모델을 학습한 것으로 3개의 파란색 데이터 포인트가 support vector들이다. 만들어지는 초평면은 해당 support vector들의 slab을 이등분함을 알 수 있다.