[ESL 리뷰] 교재 3장-5 Lasso, LARS, Forward Stagewise Selection

Least Angle Regression과 Lasso, Forward Stagewise regression과의 관계와 Lasso의 추가적인 특징들을 다뤄볼 예정이다.

The LARS/Lasso Relationship

lasso criterion은 \(R(\beta) - \frac{1}{2}\|\mathbf{y} = \mathbf{X}\beta \|^2_2 + \lambda \| \beta \|_1\)였다. \(R(\beta)\)가 미분가능하다면, \(\mathbf{x}_j ^T(\mathbf{y} - \mathbf{X}\hat{\beta}) = \lambda \cdot sign(\hat{\beta}_j)\)로, 현재 잔차와의 상관관계 \(\hat{c}_j = \mathbf{x}_j^T(\mathbf{y} - \mathbf{X}\hat{\beta})\)에 대하여 다음을 만족해야 한다.

\[sign(\hat{\beta}_j) = sign(\hat{c}_j) = s_j\]

LARS에서 현재 active set \(\mathcal{A}\)에 대하여 \(\hat{\beta}\)는 다음과 같이 업데이트가 진행되었었다.

\[\beta_j(\gamma) = \hat{\beta_j} + \gamma \hat{d}_j, \ \text{where} \ \hat{d}_j = s_jw_{\mathcal{A}_j} \ \text{if} \ j \in \mathcal{A} \ \text{else} \ 0\]

즉, \(\beta_j(\gamma)\)의 부호는 \(\gamma_j = -\hat{\beta}_j / \hat{d}_j\)에서 바뀐다. 부호가 처음으로 바뀌는 시점을 \(\tilde{\gamma}\)라고 하면,

\[\tilde{\gamma} = \underset{\gamma_j > 0}{min} \{\gamma_j\}\]

이고, \(\gamma_j\)가 모두 0보다 작으면 \(\tilde{\gamma} = \infty\)이다.

만약 \(\tilde{\gamma}\)가 \(\hat{\gamma}\)보다 작다면, \(\beta_{\tilde{j}}(\gamma)\)의 부호가 바뀌지만, \(c_{\tilde{j}}(\gamma)\)는 바뀌지 않는다. (이전에도 보았듯이, \(\gamma\)는 항상 \(|c_{\tilde{j}}(\gamma)| = \hat{C} - \gamma A_{\mathcal{A}} > 0\) 가 되도록 업데이트가 진행된다.) 따라서 Lasso에서의 \(\hat{\beta}_j, \hat{c}_j\)의 부호가 같아야 한다는 조건에 위배되기에 해당 지점에서 LARS과 Lasso의 업데이트가 달라진다. 아래 그림은 LARS와 Lasso의 coefficient profile을 비교한 것이다. 파란색 coefficient가 0이 되는 지점 이전까지는 두 그래프가 동일하다. (두 그래프 모두 piecewise-linear하기 때문에 L1 arc length는 각 스텝마다의 coefficient 변화량의 L1 norm을 모두 더한 것이다.)

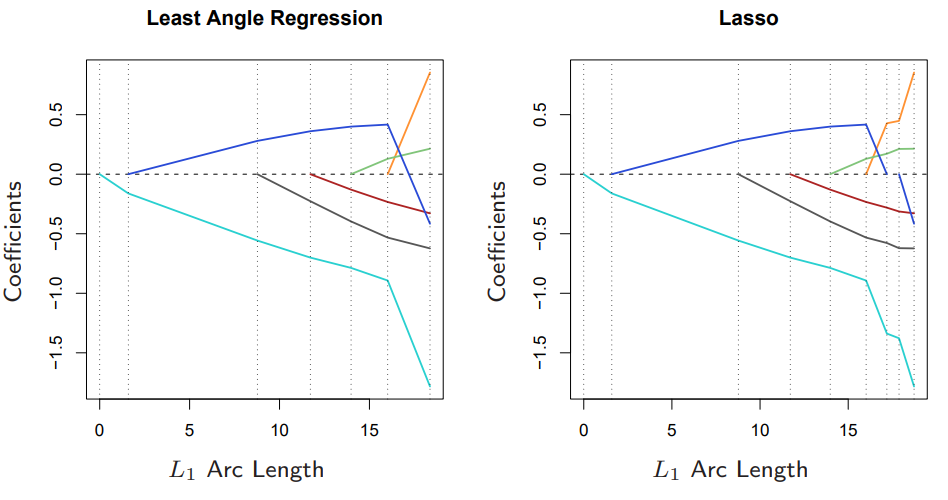
그러므로, LARS를 이용하여 Lasso를 구현하려면 다음과 같은 수정이 필요하다.

Least Angle Regression: Lasso modification

만약 \(\tilde{\gamma} < \hat{\gamma}\)라면, \(\gamma = \tilde{\gamma}\)인 지점에서 진행을 멈추고, 현재 active set \(\mathcal{A}\)에서 해당 컬럼 \(\tilde{j}\)를 제거한다. 즉,

\[\begin{align*} \hat{\mu}_{\mathcal{A}_+} &= \hat{\mu}_{\mathcal{A}} + \tilde{\gamma}\mathbf{u}_{\mathcal{A}} \ \text{and} \ \mathcal{A}_{+} = \mathcal{A} - \{ \tilde{j} \} \ \ &\text{(Lasso modification)} \\ \hat{\mu}_{\mathcal{A}_+} &= \hat{\mu}_{\mathcal{A}} + \hat{\gamma}\mathbf{u}_{\mathcal{A}} \ &\text{(Least Angle Regression)} \end{align*}\]

기존 LARS 알고리즘에서는 업데이트가 진행되면서 \(\mathcal{A}\)의 원소 수가 증가했지만, Lasso modification에서는 \(\mathcal{A}\)가 감소할 수 있다. 추가적으로 각 스텝마다 오직 하나의 인덱스가 추가되거나 제거된다는 가정을 한다면, Lasso modification알고리즘은 Lasso와 같은 결과를 내놓는다. (자세한 증명은 생략한다.)

 

The LARS/Stagewise Relationship

아래는 $p=2$일 경우 LARS와 Stagewise 알고리즘의 업데이트 방향을 나타낸 그림이다.

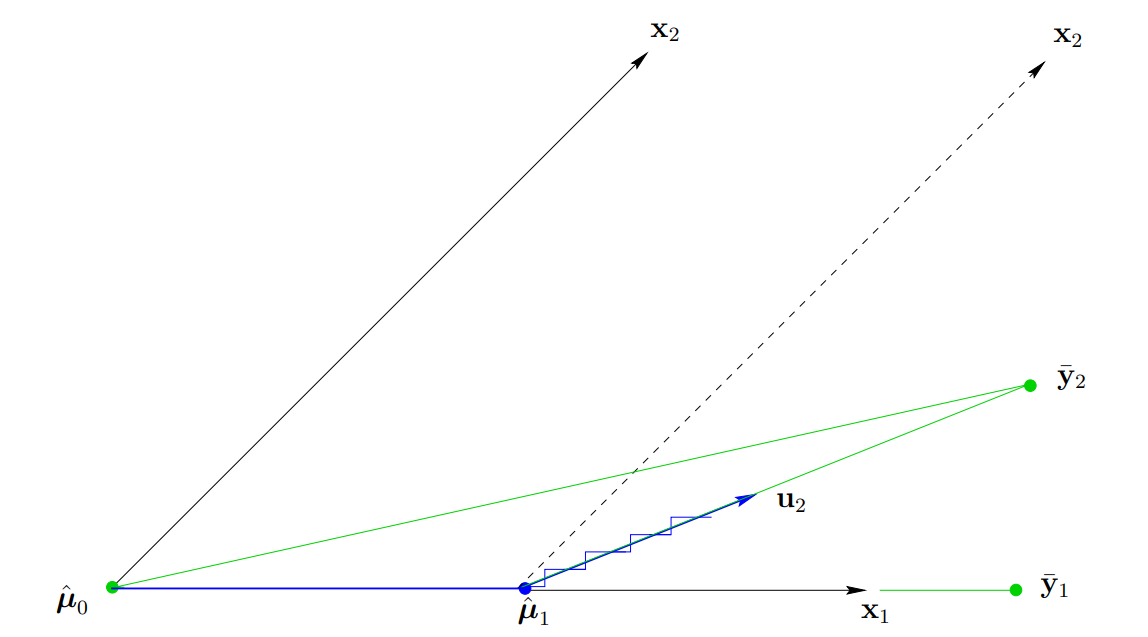
Stagewise의 경우, 각 스텝마다 계단모양으로 $\mathbf{x}_1, \mathbf{x}_2$방향으로 업데이트가 진행된다. 즉 첫 스텝에서 \(\mathbf{x}_1\)가 잔차와의 상관관계가 더 높으니 \(\hat{\mu}_1 + \epsilon \mathbf{x}_1\)으로 업데이트가 진행되고, 만약 \(\mathbf{x}_2\)와의 상관관계가 더 높을 경우, 다시 말해서 \(\mathbf{x}_2^T(\hat{\mu}_1 + \epsilon \mathbf{x}_1) > \mathbf{x}_1^T(\hat{\mu}_1 + \epsilon \mathbf{x}_1)\)이면, 이번에는 \(\epsilon \mathbf{x}_2\)를 더하여 업데이트를 진행한다. 그러므로 위 그림에서 계단 모양의 폭은 \(\epsilon\)에 의해 결정됨을 알 수 있다. 즉, \(\epsilon\)이 0에 가까운 값으로 매우 작다면 LARS와 같이 업데이트가 진행될 것이다.

이번에는 \(p>2\)인 경우를 고려해보자. 이전 스텝에서의 예측값을 \(\hat{\mu}\)라고 하고, 매우 작은 \(\epsilon\)을 통해 \(N\)번의 단계를 걸쳐 업데이트를 진행해본다고 하자. \(N\)번의 단계중 $j$번째 컬럼이 선택되어 진행된 업데이트 단계 수를 \(N_j\)라고 하자 (\(j=1,...,p\)). LARS에서 현재 스텝의 \(\hat{\mu}\)에 대해 \(\mathbf{x}_j^T(\mathbf{y} - \hat{\mu})\)를 통해 정의된 active set을 \(\mathcal{A}\)라고 할 때, 충분히 작은 \(\epsilon\)에 대하여 \(\mathcal{A}\)에 속하지 않는 $j$에 대해서는 $N_j = 0$ 이다. (아주 조금씩 움직이므로 갑자기 다른 인덱스를 사용하지는 않을 것이기에 직관적으로 그럴듯하다.) \(P = (\frac{N_1}{N}, ... , \frac{N_p}{N})\)를 정의하여, \(j \in \mathcal{A}\)인 $P$의 원소들을 골라 \(P_{\mathcal{A}}\)이면 Stagewise의 estimator는 다음과 같다.

\[\mu = \hat{\mu} + N\epsilon\mathbf{X}_{\mathcal{A}}P_{\mathcal{A}}\]

(즉, Stagewise도 LARS와 같이 sign을 고려하여 \(s_j\mathbf{x}_j\)방향으로 진행됨을 유의하자. )

LARS는 다음과 같이 업데이트가 진행되었었다.

\[\hat{\mu}_{\mathcal{A}} + \gamma\mathbf{u}_{\mathcal{A}}=\hat{\mu}_{\mathcal{A}} + \gamma\mathbf{X}_{\mathcal{A}} w_{\mathcal{A}} \ \text{ where} \ w_{\mathcal{A}} = \mathbf{A}_{\mathcal{A}}\mathbf{\mathcal{G}}_{\mathcal{A}}^{-1}1_{\mathcal{A}}\]

즉, \(P_{\mathcal{A}}\)의 원소는 음이 아니기에 \(w_{\mathcal{A}}\)의 원소가 음수일 경우에 차이가 있다. 다시말해서, Stagewise의 경우에는 업데이트 방향인 \(\mathbf{X}_{\mathcal{A}}P_{\mathcal{A}}\)가 \(\mathbf{X}_{\mathcal{A}}\)의 열벡터로 생성되는 convex cone \(\mathcal{C}_{\mathcal{A}}\)상에 놓여있다.

\[\mathcal{C}_{\mathcal{A}} = \left\{ \mathbf{v} = \sum_{j \in \mathcal{A}}s_j\mathbf{x}_jP_j, \ P_j \geq 0 \right\}\]

만약 LARS에서도 \(\mathbf{u}_{\mathcal{A}} \ \in {\mathcal{C}_{\mathcal{A}}}\)라면, LARS와 Stagewise는 같지만, 다를 경우에는 수정이 필요하다. \(\mathbf{u}_{\mathcal{A}}\)가 convex cone에 속하지 않을 경우에는 convex cone 가장 가까운 지점을 사용하는 것이 자연스러울 것이다. 즉, \(\mathbf{u}_{\mathcal{A}}\)를 \(\mathcal{C}_{\mathcal{A}}\)에 정사영시킨 단위 벡터 \(\mathbf{u}_{\mathcal{\hat{B}}}\)를 사용한다.

Least Angle Regression: Stagewise modification

만약 \(\mathbf{u}_{\mathcal{A}}\)가 \(\mathcal{C}_{\mathcal{A}}\)에 속하지 않을 경우, \(\mathbf{u}_{\mathcal{A}}\)대신, 해당 벡터를 \(\mathcal{C}_{\mathcal{A}}\)에 정사영 시킨 단위벡터 \(\mathbf{u}_{\mathcal{\hat{B}}}\)를 이용하여 업데이트를 진행한다. 마찬가지로 \(\mathcal{C}_{\mathcal{A}}\)에 속할 경우, 정사영 벡터는 원래 벡터와 같으므로 \(\mathbf{u}_{\mathcal{\hat{B}}}\)를 이용하여 업데이트를 진행한다. 즉,

\[\hat{\mu}_{\mathcal{A}_+} = \hat{\mu}_{\mathcal{A}} + \hat{\gamma}\mathbf{u}_{\mathcal{\hat{B}}}\]

\(\hat{\mathcal{B}}\)는 convex cone \(\mathcal{C}_{\mathcal{A}}\)에 사영되는 면에 해당하는 인덱스들만 모아놓은 집합으로 active set \(\mathcal{A}\)의 부분집합이다. \(\mathbf{u}_{\hat{\mathcal{B}}}\)는 모든 \(j \in \hat{\mathcal{B}}\)에 대한 \(\mathbf{x}_j\)들의 equiangular vector이다. active set으로 \(\hat{\mathcal{B}}\)를 사용하기에, 업데이트마다 두개 이상의 인덱스가 제거될 수도 있다.

 

Note. 다시 생각해보자면, Stagewise의 경우의 업데이트 과정은 다음과 같다.

\[\beta_j \leftarrow \beta_j + \epsilon s_j \ \text{and} \ \hat{\mu} \leftarrow \hat{\mu} + \epsilon s_j\mathbf{x}_j\]

즉, 항상 잔차와의 상관관계의 방향으로 업데이트가 진행된다. 하지만 LARS의 경우 \(w_{\mathcal{A}}\)의 원소에 의해 이와 반대방향으로 업데이트가 진행 될 수 있다. 따라서 ESL 교재에서는 같은 방향에 대해서만 업데이트를 진행하도록 제약조건을 걸어 LARS알고리즘을 수정하였다. 교재에서의 수정된 알고리즘은 다음과 같다. (마찬가지로 자세한 증명은 생략한다.)

Comparison of LARS, Lasso, Stagewise

세 알고리즘 LARS, Lasso, Stagewise의 차이점은 각각 다음과 같다.

• Stagewise: 연속적으로 correlation \(\hat{c}_j = \mathbf{x}_j^T(\mathbf{y} - \hat{\mu})\)과 같은 부호를 갖도록 \(\hat{\beta}_j\)가 움직인다.
• Lasso: \(\hat{\beta}_j\)는 항상 \(\hat{c}_j\)와 부호가 갖다.
• LARS: 부호에 대한 제한이 없다.

이러한 관점에서 볼 때, Lasso는 LARS와 Stagewise의 중간단계이다.

Note. Lasso에서는 $k$번째 스텝마다, \(sign(\hat{\beta}_k) = sign(\hat{c}_k)\)를 만족시켜야 했다. LARS의 경우 만약 현재 단계에서 하나의 인덱스 $k$만이 추가된다다면, \(sign(\hat{\beta}_{kk}) = sign(\hat{c}_{kk})\)를 만족한다. 즉 추가된 하나의 인덱스에 대해서만 lasso와 같은 부호의 제한조건을 만족한다. 증명과정은 다음과 같다.

\(\hat{\beta}_{kk} = \hat{\beta}_{k-1,k} + \hat{\gamma}_kw_{kk}\)로 업데이트되고 \(\hat{\beta}_{k-1,k} = 0\)임을 유의하면, \(w_{kk}\)의 부호가 양수임을 보이면 충분하다. 이전 LARS 관련 포스팅에서도 보였듯이 \(w_k\)를 다음과 같이 나타낼 수 있다.

\[w_k = \frac{\mathbf{A}_k}{\hat{C}_k}\left[ \mathcal{G}_k^{-1}\mathbf{X}_k^T(\mathbf{y} - \hat{\mu}_{k-1}) \right] = \lambda w_k^* \ \text{where} \ w_k^* = \mathcal{G}_k^{-1}\mathbf{X}_k^T(\mathbf{y} - \hat{\mu}_{k-1}) , \lambda >0\]

즉 \(w_k^*\)가 양수임을 보여야 한다. \(k-1\)번째 OLS estimator를 \(\bar{\mathbf{y}}_{k-1}\)라고 하면, 이에 대한 잔차는 \(\mathbf{X}_{k-1}\)의 컬럼벡터들과 수직을 이루고 \(s_k\mathbf{x}_k\)와의 내적값은 0보다 크다는 것을 알 수 있다. 따라서

\[\mathbf{X}_k^T(\mathbf{y} - \bar{\mathbf{y}}_{k-1}) = (0_{k-1}, \delta)^T \ \text{with} \ \delta >0\]

임을 알 수 있다. 그러므로,

\[\begin{align*} w_k^* &= \mathcal{G}_k^{-1}\mathbf{X}_k^T(\mathbf{y} - \bar{\mathbf{y}}_{k-1} + \bar{\mathbf{y}}_{k-1} - \hat{\mu}_{k-1}) \\ &= \mathcal{G}_k^{-1}(0_{k-1}, \delta)^T + (\bar{\gamma}_{k-1} - \hat{\gamma}_{k-1})\mathcal{G}_k^{-1}\mathbf{X}_k^T \mathbf{u}_{k-1} \end{align*}\]

이다. 먼저 \(\mathbf{u}_{k-1}\)은 \(\mathbf{X}_{k-1}\)의 열공간에 속하므로 두번째 항의 $k$번째 원소는 0이다. 또한 \(\mathcal{G}_k\)는 positive definite이므로, 역행렬도 마찬가지로 positive definite이다. 즉,

\[(0_{k-1}, \delta) \mathcal{G}_k^{-1}(0_{k-1}, \delta)^T = \delta^2(\mathcal{G}_k^{-1})_{kk} > 0\]

이므로, \(\mathcal{G}_k^{-1}(0_{k-1}, \delta)^T\)의 $k$번째 원소인 \(\delta(\mathcal{G}_k^{-1})_{kk}\)도 마찬가지로 양수임을 알 수 있다. 그러므로 \(w_{kk}^*\)는 양수이므로, 마찬가지로 \(w_{kk}\)도 양수이다.

 

Further Properties of the Lasso

다음으로 Lasso와 관련된 여러 특징들을 다뤄볼 예정이다.

Piecewise-Linear Path Algorithms

LARS는 Lasso의 solution path가 piecewise linear하다는 특징을 이용하였다. 규제 문제에서 다음과 같은 \(\hat{\beta}(\lambda)\)를 푼다고 가정하자.

\[\begin{align*} \hat{\beta}(\lambda) &= \underset{\beta}{argmin} \left[ R(\beta) + \lambda J(\beta) \right] \\ \text{with} \\ R(\beta) &= \sum_{i=1}^N L(y_i, \beta_0 + \sum_{j=1}^p x_{ij}\beta_j) \ \text{where both} \ L,J \ \text{are convex} \end{align*}\]

다음 2가지 조건은 \(\hat{\beta}(\lambda)\)의 solution path가 piecewise linear임을 만족하는 충분조건이다.

1. \(R\)은 \(\beta\)에 대한 quadratic function (or piecewise-quadratic function)이다.
2. \(J\)는 \(\beta\)에 대해 piecewise linear하다.

위 조건은 또한 solution path가 효율적으로 계산될 수 있음을 내포하고 있다. 이를 만족하는 예로는 MSE, MAE, Huberized losses, \(\beta\)에 대한 \(L_1, L_{\infty}\) penalty, hinge loss등이 있다.

The Dantzig Selector

Candes와 Tao(2007)는 다음과 같은 criterion을 제안하였다.

\[\underset{\beta}{min} \|\beta\|_1 \text{ subject to } \| \mathbf{X}^T(\mathbf{y} - \mathbf{X}\beta)\|_{\infty} \leq s\]

이에 대한 해를 Dantzig selector(DS)라고 부른다. 위 문제는 다시 다음을 푸는 것과 동치이다.

\[\underset{\beta}{min} \| \mathbf{X}^T(\mathbf{y} - \mathbf{X}\beta)\|_{\infty} \text{ subject to } \|\beta\|_1 \leq t\]

\(\| \cdot \|_{\infty}\)는 \(L_{\infty}\) norm으로 벡터의 원소의 절대값 중 가장 큰 값이다. 위 식은 Lasso에서 MAE를 gradient의 가장 큰 절대값으로만 대체했다는 점에서 Lasso와 상당히 유사하다. DS도 마찬가지로 \(p < N\)일 경우에 \(t\)가 충분히 큰 값을 가지면 least squares solution과 동일하다. 또한 \(p \geq N\)일 경우에 둘 모두 \(L_1\) norm을 최소화하는 least squares solution을 갖는다. 하지만 \(t\)가 작을 경우에는, DS와 Lasso는 다른 solution path를 갖는다. Candes와 Tao는 DS가 Linear Programming(LP) 문제임을 보였고, sparse한 \(\beta\)를 해결할 수 있음을 증명하였다. 이는 이후에 Lasso에 대해서도 동일하게 Bickel에 의해 증명되었다. (2008).

하지만 DS는 Lasso에 비해 합리적이지 않고 prediction error를 낮출 수 있는 특징이 있다. Lasso의 경우에서는 LARS와 같이 현재 active set \(\mathcal{A}\)에 속한 피쳐 벡터들과 잔차와의 상관관계가 모두 같고, active set에 속하지 않은 벡터들보다는 항상 크게 유지되었다. 또한 스텝이 진행될 때마다 상관관계는 단조감소하였다. DS의 경우에는 위 식을 보면 알 수 있듯이, 현재 잔차와의 상관관계가 가장 높은 벡터와의 상관관계를 최소화하는 방향으로 업데이트가 진행된다. 따라서 Lasso에서보다 잔차와의 가장 상관관계가 높은 값이 작을 수 있지만, 이 과정에서 이상한 현상이 일어난다. 만약 현재 active set의 크기가 $m$이라면, 잔차와의 상관관계가 가장 큰 $m$개의 피쳐가 존재한다. 하지만 해당 $m$개의 벡터는 모두 active set에 있다는 것을 보장할 수 없다. 따라서 잔차와의 상관관계가 더 작은 벡터를 이용하여 업데이트가 진행될 수 있다.

Sparsity

\(p>N\)인 경우에 $t$가 클 때의 Lasso의 solution에 대해 다뤄보자. 이 때 \(\mathbf{X}\)에 대해 몇몇의 가정을 추가한다면, true model이 sparse할 경우, lasso solution은 높은 확률로 correct predictor이다. 자세한 내용은 여기 section 4를 참고하자.

만약 \(\mathbf{X}\)가 어떠한 \(\epsilon \in (0,1]\)에 대하여 다음을 만족한다고 하자.

\[\| (\mathbf{X}_{\mathcal{S}}^T\mathbf{X}_{\mathcal{S}})^{-1}\mathbf{X}_{\mathcal{S}}^T\mathbf{X}_{\mathcal{S}^c} \|_{\infty} \leq (1-\epsilon)\]

\(\mathcal{S}\)는 true model에서 coefficient가 0이 아닌 인덱스들을 모아놓은 집합이다. 이를 다시 쓰면 다음과 같다.

\[\| (\mathbf{X}_{\mathcal{S}}^T\mathbf{X}_{\mathcal{S}})^{-1}\mathbf{X}_{\mathcal{S}}^T\mathbf{x}_{j} \|_{1} \leq (1-\epsilon) \text{ for } j \notin \mathcal{S} \ \text{ (Mutual incoherence)}\]

이는 즉, 회귀분석에서 필요가 없는 변수들은 active set의 변수들과 높은 상관관계를 갖지 않는다는 조건이다.

active variables들을 다루는데 있어서 lasso는 shrinkage effect가 있기에 0에 가까운 값으로 coefficients가 줄어들어 bias가 생기게 된다. 이로 인해 생기는 bais를 줄이는 방법으로는 먼저, Lasso를 통해 acitive set을 찾고 해당 변수들을 사용하여 least squares solution을 구하는 방법이 있다. 하지만 이 방법은 선택된 active set이 마찬가지로 $N$보다 클 경우 적절하지 않을 수 있다. 이에 대한 대안으로는 전과 마찬가지로 먼저 lasso를 진행하여 active set을 구한 후에 해당 active set을 이용하여 한번 더 lasso를 진행하는 방법이 있다. 이를 relaxed lasso라고 한다. complexity paramet인 \(\lambda\)는 두 번의 lasso에서 모두 cross validation을 통해 구한다. 두번째 lasso의 경우에서는 noisy한 변수들이 앞선 lasso에 의해 어느정도 제거되었으므로 더 작은 \(\lambda\)를 갖을 것이라는 가정을 해볼 수 있고, 따라서 약한 규제를 적용하기에 shrinkage effect가 완화될 것이다. 마지막으로, 또 다른 대안으로는 lasso penalty function을 더 큰 coefficient를 가지는 인덱스에 대해서는 규제를 완화하도록 수정하는 방법이 있다. 이에 대한 예로 아래의 smootly clipped absolute deviation(SCAD) penalty가 있다.

\[\text{replaces } \lambda |\beta| \text{ by } J_{a}(\beta,\lambda) \text{ where} \\ \frac{dJ_{a}(\beta,\lambda)}{d\beta} = \lambda \cdot sign(\beta)\left[ I(|\beta| \leq \lambda) + \frac{(a\lambda - |\beta|)_+}{(a-1)\lambda}I(|\beta| > \lambda) \right] \text{ for some } a \geq 2\]

위 식의 대괄호 안 두번째 항 덕분에 coefficient가 클 경우 shrinkage가 줄어들며, \(a \rightarrow \infty\)이면 shrinkage가 일어나지 않는다.

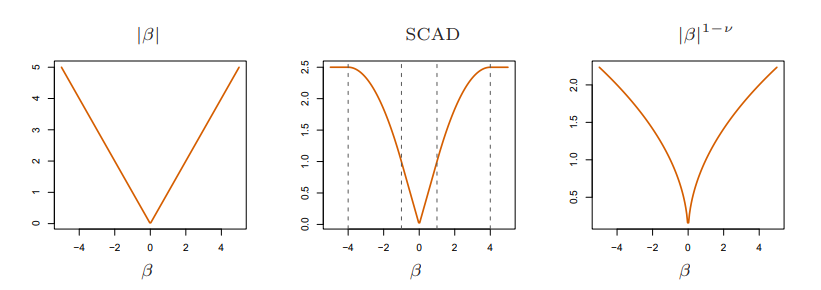
하지만 위 그림처럼 SCAD는 non-convex하기 때문에 계산과정이 복잡하다. (SCAD의 경우 \(\lambda = 1, a=4\), 마지막 그림의 \(\nu=0.5\)이다.) The adaptive lasso는 penalty 항에 가중치 \(w_j = 1/ \|\hat{\beta}_j\|_1^{\nu}\) (\(\hat{\beta}_j\)는 least squares estimator, \(\nu\)>0) 를 추가한 방법인데, 이는 \(\|\beta\|_1^q\) (\(q = 1-\nu\)) penalty에 대한 근사치이다. 해당 penalty는 위 그림을 보면 SCAD와 비슷한 shrinkage를 보이기에, The adaptive lasso는 convexity를 유지하면서 active variable들에 대한 shrinkage로 발생하는 bias를 줄여 consistent estiamates를 내놓는다.

Pathwise Coordinate Optimization

Coordinate descent 알고리즘을 이용하여 Lasso를 구현할 수 있다. 먼저, complexity parameter \(\lambda\)를 고정하여 \(\beta_j\)들을 업데이트하여, \(\beta\)가 수렴할 때 까지 점진적으로 \(\lambda\)를 업데이트한다.

\(\mathbf{X}\)가 standardized하다고 가정하자. \(\lambda\)에 대하여 \(j\)번째 coordiante를 고정해 업데이트를 진행한다면, 나머지 항을 고려하지 않고 다음과 같이 나타낼 수 있다.

\[\begin{align*} R(\tilde{\beta}(\lambda), \beta_j) &= \frac{1}{2}\sum_{i=1}^N \left( y_i - \sum_{k \neq j}x_{ik}\tilde{\beta}_k(\lambda) - x_{ij}\beta_j \right)^2 + \lambda \sum_{k \neq j} | \tilde{\beta}_k(\lambda) | + \lambda|\beta_j| \\ &= \frac{1}{2}\sum_{i=1}^N \left(y_i - \tilde{y}^{(j)}_i - x_{ij}\beta_j \right)^2 + \lambda|\beta_j| + C \end{align*}\]

즉, \(\mathbf{x}_{j}\)와 \(\mathbf{y} - \tilde{\mathbf{y}}^{(j)}\) 대한 univariate case이므로 다음과 같이 업데이트를 진행할 수 있다. (\(\beta_j\)에 대하여 미분하여 0이 되는 지점을 찾은 것이다.)

\[\tilde{\beta}_j (\lambda) \leftarrow sign(\sum_{i}x_{ij}(y_i - \tilde{y}_j^{(j)})) \left(|\sum_{i}x_{ij}(y_i - \tilde{y}_j^{(j)})| - \lambda \right)_+ \text{ where } x_+ = min(x,0)\]

따라서 초기 \(\lambda\)값은 \(\beta\)가 0이되는 값들 중에 가장 작은 값을 골라서, 점진적으로 \(\lambda\)를 줄여나가면서 \(\beta\)가 수렴할 때 까지 업데이트를 진행한다. Coordinate descent 알고리즘은 패널티 항에 각각의 파라미터를 더한 Elastic net, the grouped lasso등 다양한 모델에서도 적용될 수 있다.