“The Elements of Statistical Learning” 교재 3장 section 3.5 Methods Using Derived Input Directions에 관해 정리해보았다.
우리의 input이 많은 변수를 가지고 있다면, 서로 높은 상관관계를 가질 가능성이 높다. 따라서 기존 input 변수들인 $X_j, \ j=1,…,p \ $들의 선형 결합을 통해 $Z_m, \ m=1,…,M \ $을 만들어, 이를 새로운 input으로 사용하여 회귀모델에 적용할 것이다. (당연히 더 적은 수의 변수를 만드는 것이므로 $M$은 $p$보다 작거나 같아야 할 것이다.) 이전 포스팅들과 마찬가지로, input vector들은 모두 표준화를 시켰다고 가정한다.
Principal Components Regression
PCA는 선형결합인 $Z_m$을 이전 Ridge에 대해 다룬 포스팅에서 정의했던, 주성분(principal component)을 사용한다. 다시 복습해보자면 $\mathbf{X}$의 특이값 분해를 $\mathbf{X} = \mathbf{U} \mathbf{D} \mathbf{V}^T $라 할 때, 공분산 행렬은 $\mathbf{S} = \frac{1}{N} \mathbf{X}^T \mathbf{X}=\frac{1}{N} \mathbf{V}\mathbf{D}^2\mathbf{V}^T$이다. $\mathbf{X}$의 주성분은 분산을 최대한 보존하는 직교 기저 $\mathbf{Z} = ( \mathbf{z}_1,\mathbf{z}_2,…,\mathbf{z}_M ), \ \mathbf{z}_m = \mathbf{X}v_m$이다.
이전 포스팅에서 봤듯이, 첫번째 주성분인 $\mathbf{z}_1$에 대해 $Var(\mathbf{z}_1) = \frac{d_1^2}{N}$이고, $\mathbf{z}_1 = \mathbf{X}v_1 = \mathbf{u}_1d_1$이다. 즉 $v_1$은 $\mathbf{S}$의 가장 큰 고윳값에 대응하는 고유벡터였다. 다음 주성분들은 이전 주성분 벡터들과 직교이면서 분산이 가장 큰 벡터들이다. 즉 $m$번째 주성분 벡터를 찾는 과정은 다음과 같다.
\[\begin{align*} v_m &= \underset{\alpha}{\mathrm{argmax}} \ Var(\mathbf{X}\alpha) \ \text{subject to} \ \|\alpha\|=1, \ \alpha^T\mathbf{S}v_l = 0 \ \text{for} \ l=1,..,m-1 \\ z_m &= Xv_m \end{align*}\]여기서 두번째 제약조건은 $\mathbf{z}_m$이 이전 주성분 벡터들과 수직임을 보장하는 것이다. $(\alpha^T\mathbf{S}v_l = \alpha^T \mathbf{X}^T\mathbf{X}v_l = \langle \mathbf{X}\alpha, \mathbf{X}v_l \rangle )$
이전 포스팅에서 살펴봤듯이, principal component direction인 $v_m$은 $\mathbf{V}$의 컬럼벡터($\mathbf{S}$의 고유벡터)였다.이는 수학적 귀납법을 사용하여 증명할 수 있다. $m$이 1인 경우는 위에서 확인했으므로, $m=k-1$까지 모두 성립할 때 $m=k$도 성립하는지 확인해보자.
$\lambda_{1},…,\lambda_{k-1}$을 $\mathbf{S}$의 가장 큰 $k-1$개의 고유값이라고 하자. $v_k$는 다음과 같다.
\[\underset{\alpha}{\mathrm{argmax}} \ \alpha^T\mathbf{S}\alpha \ \text{subject to} \ \|\alpha\|=1, \ \alpha^T\mathbf{S}v_l = 0 \ \text{for} \ l=1,..,k-1\]이를 라그랑주 승수법으로 나타내면 다음과 같다.
\[\mathcal{L} = \alpha^T\mathbf{S}\alpha - \lambda(\alpha^T\alpha - 1) + \sum_{l=1}^{k-1}c_l\alpha^T\mathbf{S}v_l\]$v_k$는 위 식을 최대화하므로, 이를 $\alpha$에 대하여 편미분하여 $v_k$를 대입하면 0이다.
\[\begin{align*} \frac{\partial \mathcal{L}}{\partial \alpha} &= 2\mathbf{S}\alpha - 2\lambda\alpha + \sum_{l=1}^{k-1}c_l\mathbf{S}v_l \\ \frac{\partial \mathcal{L}(\alpha=v_k)}{\partial \alpha} &= 2\mathbf{S}v_k - 2\lambda v_k + \sum_{l=1}^{k-1}c_l\mathbf{S}v_l = 0 \end{align*}\]임의의 $v_j, \ j=1,…,k-1$에 대하여, 위 식의 양변에 $v_j^T\mathbf{S}$를 곱하면 다음과 같다.
\[\begin{align*} 0 &= 2v_j^T\mathbf{S}^2v_k - 2\lambda v_j^T\mathbf{S}v_k + \sum_{l=1}^{k-1}c_lv_j^T\mathbf{S}^2v_l \\ &= 2(\mathbf{S}v_j)^T\mathbf{S}v_k + c_jv_j^T\mathbf{S}v_j \\ &= 2\lambda_j v_j^T\mathbf{S}v_k + c_jv_j^T\mathbf{S}v_j \\ & =c_jv_j^T\mathbf{S}v_j = c_jv_j^T\lambda_j v_j = c_j\lambda_j \ \text{for} \ \forall j \end{align*}\]즉, 모든 $c_j$가 0이므로, 이를 $\mathcal{L}$을 편미분한 식에 대입하면 다음이 성립한다. 즉 $\lambda$는 $\mathbf{S}$의 고유값이고, $v_k$는 이에 대응하는 고유벡터이다.
\[\mathbf{S}v_k = \lambda v_k\]따라서 PCR은 다음과 같이 진행된다.
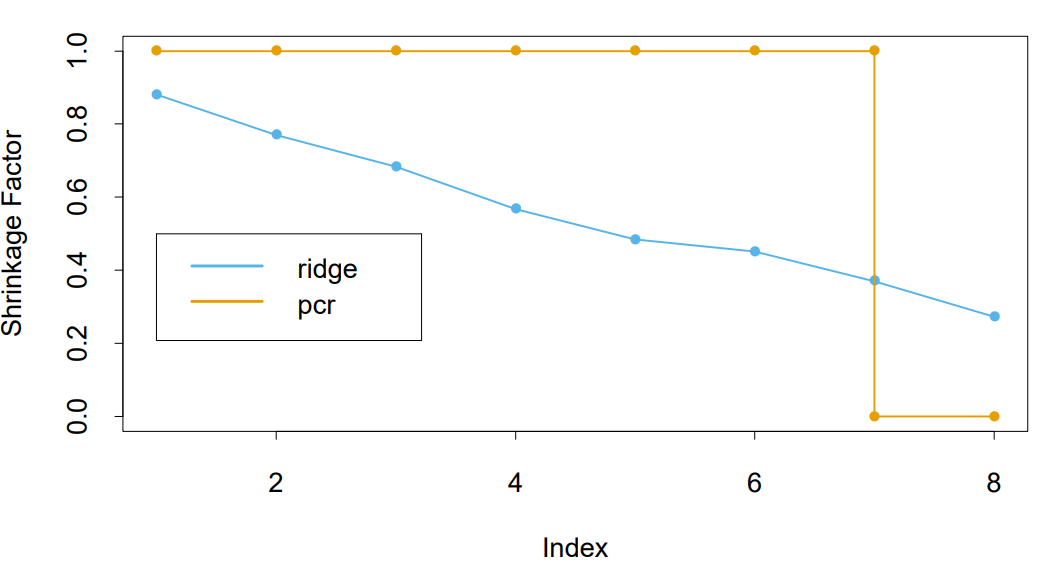
\[\begin{align*} \hat{\mathbf{y}}^{pcr}_{(M)} &= \bar{y}\mathbf{1} + \sum_{m=1}^M \hat{\theta}_m\mathbf{z}_m \ \text{where} \ \hat{\theta}_m = \frac{\langle \mathbf{z}_m, \mathbf{y} \rangle}{\langle \mathbf{z}_m, \mathbf{z}_m \rangle} \\ &= (\mathbf{1} \ \mathbf{X})\begin{pmatrix} \bar{y} \\ \sum_{m=1}^M \hat{\theta}_m\mathbf{z}_m \end{pmatrix} \end{align*}\]즉 $\hat{\beta}^{pcr}(M) = \sum_{m=1}^M \hat{\theta}_mv_m$이다. 또한 $\mathbf{Z} = \mathbf{X}\mathbf{V} = \mathbf{U}\mathbf{D}$이므로, $M=p$일 경우 완전히 OLS의 식과 같다. 아래 그림은 prostate 데이터를 이용해 릿지 회귀와 PCR을 비교한 것으로 두 모델이 상당히 유사한 것을 알 수 있다. 차이점은 릿지는 변수를 점진적으로 줄이고, PCR은 완전히 제거해버린다는 점이다. 책에서는 이를 각각 shirinkage and truncation patterns (또는 shrink smoothly and discrete step)이라고 표현하였다.
Partial Least Squares
PLS는 PCR과 다르게 $\mathbf{z}_m$을 구성하는데 있어서 input vector들의 선형결합만이 아닌 추가적으로 $\mathbf{y}$를 추가한 선형결합을 사용한다.
매 단계마다, $\hat{\phi}_{mj} = \langle \mathbf{x}_j^{m-1}, \mathbf{y} \rangle$를 만들어 \(\mathbf{z}_m = \sum_j \hat{\phi}_{mj}\mathbf{x}_j\) 를 업데이트 하고, $\mathbf{x}_j^{m-1}$을 $\mathbf{z}_m$에 대해 직교화한다. 전체적인 과정은 다음과 같다.

PLS도 PCR과 마찬가지로 $M=p$일 경우, OLS의 해와 같다. 또한 input vector들이 서로 직교한다면 첫번째 스텝에서 종료되어 OLS의 해를 갖는다. 다음 스텝인 $m > 1$인 경우에 $\hat{\phi}_{mj}$가 모두 0이 되어 업데이트가 이뤄지지 않기 때문인데 유도과정은 다음과 같다.
\[\begin{align*} \hat{\phi}_{2,j} &= \langle \mathbf{x}_j - \frac{\langle \mathbf{z}_m, \mathbf{x}_j \rangle}{\langle \mathbf{z}_m, \mathbf{z}_m \rangle}\mathbf{z}_m, \mathbf{y} \rangle \ \text{where} \ \mathbf{z}_m = \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle \mathbf{x}_j \\ \langle \mathbf{z}_m, \mathbf{z}_m \rangle &= \langle \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle \mathbf{x}_j, \sum_{k=1}^p \langle \mathbf{x}_k, \mathbf{y} \rangle \mathbf{x}_k \rangle = \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle^2 \langle \mathbf{x}_j, \mathbf{x}_j \rangle = \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle^2 \\ \langle \mathbf{z}_m, \mathbf{x}_j \rangle &= \langle \mathbf{x}_j, \mathbf{y} \rangle \langle \mathbf{x}_j, \mathbf{x}_j \rangle = \langle \mathbf{x}_j, \mathbf{y} \rangle \\ \langle \mathbf{z}_m, \ \mathbf{y} \rangle &= \langle \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle\mathbf{x}_j, \mathbf{y} \rangle = \sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle^2 \\ \end{align*}\]즉, 이를 $\hat{\phi}_{2j}$에 대입하면 다음과 같다.
\[\begin{align*} \hat{\phi}_{2,j} &= \langle \mathbf{x}_j - \frac{\langle \mathbf{z}_m, \mathbf{x}_j \rangle}{\langle \mathbf{z}_m, \mathbf{z}_m \rangle}\mathbf{z}_m, \mathbf{y} \rangle = \langle \mathbf{x}_j, \mathbf{y} \rangle - \frac{\langle \mathbf{z}_m, \mathbf{x}_j \rangle}{\langle \mathbf{z}_m, \mathbf{z}_m \rangle}\langle \mathbf{z}_m , \mathbf{y} \rangle \\ &= \langle \mathbf{x}_j, \mathbf{y} \rangle - \frac{\langle \mathbf{x}_j, \mathbf{y} \rangle}{\sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle^2}\sum_{j=1}^p \langle \mathbf{x}_j, \mathbf{y} \rangle^2 \\ &= \langle \mathbf{x}_j, \mathbf{y} \rangle - \langle \mathbf{x}_j, \mathbf{y} \rangle = 0 \end{align*}\]PLS는 $\mathbf{z}$의 분산만이 아닌, 추가적으로 $\mathbf{y}$와의 상관관계를 최대화하는 방향으로 $\hat{\phi}$가 정해진다. $m$번째 PLS의 방향 $\hat{\phi}_m$는 다음과 같다.
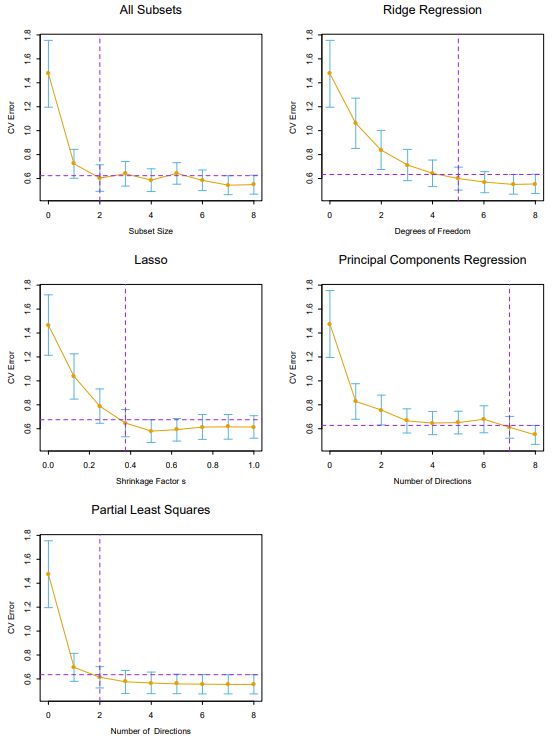
\[\begin{align*} \hat{\phi}_m &= \underset{\alpha}{\mathrm{argmax}} \ Corr^2(\mathbf{y}, \mathbf{X}\alpha)Var(\mathbf{X}\alpha) \ \text{subject to} \ \|\alpha\|=1, \ \alpha^T\mathbf{S}\hat{\phi}_l = 0 \ \text{for} \ l=1,..,m-1 \\ &= \underset{\alpha}{\mathrm{argmax}} \ Cov^2(\mathbf{y}, \mathbf{X}\alpha) \ \text{subject to} \ \|\alpha\|=1, \ \alpha^T\mathbf{S}\hat{\phi}_l = 0 \ \text{for} \ l=1,..,m-1 \\ &= \underset{\alpha}{\mathrm{argmax}} \ (\mathbf{y}^T\mathbf{X}\alpha)^2 \ \text{subject to} \ \|\alpha\|=1, \ \alpha^T\mathbf{S}\hat{\phi}_l = 0 \ \text{for} \ l=1,..,m-1 \end{align*}\]아래는 prostate 데이터를 이용하여 subset selection, shrinkage method들을 비교한 그림이다. 릿지 회귀와 PCA, PLS 셋 모두 비슷하게 움직이는 것을 볼 수 있다.
Continuum Regression
CR은 OLS, PCR, PLS를 일반화한 모델이다. 각각의 세 모델들은 CR의 파라미터에 특정값을 넣었을 때의 경우이다. CR과 RR(릿지 회귀)는 상당히 유사한데 이를 통해 릿지 회귀와 PCR, PLS간의 유사성을 확인해 볼 수 있다.
CR은 non-negative인 CR 파라미터 $\gamma$에 대해 다음과 같은 $c = c(\gamma)$를 찾는 것이다.
\[\begin{align*} c &= \underset{c}{\mathrm{argmax}} \ T = \underset{c}{\mathrm{argmax}} (c^Ts)^2(c^TSc)^{\gamma - 1} \ \text{subject to} \ \|c\|=1 \ \text{where} \ s= \mathbf{X}^T\mathbf{y}, S = \mathbf{X}^T\mathbf{X} \\ &= \underset{c}{\mathrm{argmax}} \ Cov^2(\mathbf{X}c, \mathbf{y})Var(\mathbf{X}c)^{\gamma -1} \ \text{subject to} \ \|c\|=1 \end{align*}\]$c$를 구했으면 기존 input vector들의 선형결합을 통해 새로운 input $\mathbf{X}c$를 이용하여 회귀계수를 구한다. 즉 $\gamma = 0$일 경우, 상관관계를 최대화하는 것이므로 OLS이고, $\gamma = 1$일 경우에는 공분산을 최대화 하는 것이므로 PLS의 $\hat{\phi}_1$, $\gamma \rightarrow \infty$일 경우에는 분산만 고려하는 것이므로 PCR의 $v_1$ 과 같다. CR도 PCR,PLS와 마찬가지로 이후의 $c$들은 위 조건들을 만족하면서 추가적으로 이전 벡터들과 직교를 이루는 방향으로 선택하여, $w$개의 벡터들이 선택되면 알고리즘을 종료한다. 즉 $\gamma$와 $w$ 두 개의 파라미터로 학습이 이뤄지고, 이 두 파라미터는 cross validation을 통해 적절한 파라미터를 찾는다.
Note. 릿지 회귀의 경우 회귀계수는 $\hat{\beta}^{RR}(\delta) = (S + \delta I)^{-1}s$ 로 OLS에서 $S$의 역행렬을 구할 수 없을 경우에도 구할 수 있다는 걸 이전 포스팅에서 유도했었다.
$\gamma \in [0,1)$에 대해 CR의 first factor인 $c_1$으로부터의 회귀계수를 $\hat{\beta}^{CR}(\gamma)$라고 할 때, RR의 회귀계수와는 다음과 같은 관계가 성립한다. 또한 $\delta, \gamma$의 관계도 다음과 같다.
\[\begin{align*} \hat{\beta}^{CR}(\gamma) &= (1 + \frac{\gamma}{1-\gamma})\hat{\beta}^{RR}(\delta), \\ \delta(\gamma) &= \tilde{e}(\gamma)\frac{\gamma}{1-\gamma} \ \text{where} \ \tilde{e}(\gamma) = \frac{\hat{\beta}^{CR}(\gamma)^TS\hat{\beta}^{CR}(\gamma)}{\hat{\beta}^{CR}(\gamma)^T\hat{\beta}^{CR}(\gamma)} \end{align*}\]$\tilde{e}(\gamma)$는 $S$의 고유값들의 가중평균으로 $\gamma$에 대한 단조 증가 함수이다.
증명과정은 다음과 같다. 먼저 $c$를 구해야 하므로 $T$를 최대화 하는 벡터를 찾아야 한다. T에 로그를 씌워 라그랑주 승수법을 풀면 다음과 같다.
\[\begin{align*} \mathcal{L} &= 2\log(c^Ts) + (\gamma - 1) \log(c^TSc) - \lambda(c^Tc-1) \\ \frac{\partial \mathcal{L}}{\partial c} &= 2 s(c^Ts)^{-1} + 2(\gamma-1)Sc(c^TSc)^{-1} - 2\lambda c = 0 \end{align*}\]위 편미분 식의 양변에 $c^T$를 곱하면 다음과 같다.
\[0 =c^Ts(c^Ts)^{-1} + 2(\gamma-1)c^TSc(c^TSc)^{-1} - 2\lambda c^Tc = I + (\gamma-1)I - \lambda I = (\gamma - \lambda)I\]즉, $\lambda = \gamma$ 이다. 또한 $c^Ts$와 $c^TSc$는 스칼라이므로 이들을 무시하여 $s$와 $c$에 대해 다음과 같이 쓸 수 있다.
\[\begin{align*} ((\frac{1 - \gamma}{c^TSc})S + \gamma I) c &= (c^Ts)^{-1}s \\ c &\propto ((\frac{1 - \gamma}{c^TSc})S + \gamma I)^{-1}s \\ c &\propto (S + \delta I)^{-1}s=\hat{\beta}^{RR}(\delta) \ \text{where} \ \delta = \frac{c^TSc}{1-\gamma}\gamma \end{align*}\]즉 $c$는 RR의 회귀 계수와 비례하고 $c^Tc=1$이라는 제약조건을 사용하여 $\delta, \gamma$간의 비례식은 다음과 같다.
\[\delta(\gamma)= \frac{c^TSc}{c^Tc}\frac{\gamma}{1-\gamma}\]이제 $c$를 구했으니 새로운 input vector $\mathbf{X}c$ 를 이용한 회귀 계수를 구하면 다음과 같다.
\[\hat{\beta}^{CR}(\gamma) = \frac{\langle \mathbf{X}c, \mathbf{y} \rangle}{\langle \mathbf{X}c, \mathbf{X}c \rangle}c = \frac{c^Ts}{c^TSc}c\]이는 $c$의 스케일에 영향을 받지 않으므로, 위에서 유도한 비례식을 등식으로 바꾸어 대입하면 다음과 같다.
\[\begin{align*} \frac{c^Ts}{c^TSc} &= \frac{c^T(S+\delta I)c}{c^TSc} = 1 + \frac{c^T c}{c^TSc}\delta = 1 + \frac{\gamma}{1-\gamma} \\ c &= \hat{\beta}^{RR}(\delta) \end{align*}\]따라서 이들을 $\hat{\beta}^{CR}(\gamma), \ \delta(\gamma)$ 에 대입하면 다음과 같다.
\[\begin{align*} \hat{\beta}^{CR}(\gamma) &= \frac{c^Ts}{c^TSc}c = (1 + \frac{\gamma}{1-\gamma})\hat{\beta}^{RR}(\delta), \\ \delta(\gamma) &= \frac{c^TSc}{c^Tc}\frac{\gamma}{1-\gamma} = \frac{\hat{\beta}^{RR}(\delta)^TS\hat{\beta}^{RR}(\delta)}{\hat{\beta}^{RR}(\delta)^T\hat{\beta}^{RR}(\delta)}\frac{\gamma}{1-\gamma}\\ &=\frac{\hat{\beta}^{CR}(\gamma)^TS\hat{\beta}^{CR}(\gamma)}{\hat{\beta}^{CR}(\gamma)^T\hat{\beta}^{CR}(\gamma)} = \tilde{e}(\gamma)\frac{\gamma}{1-\gamma} \end{align*}\]Discussion on Ridge regression and Continuum regression
Note. OLS의 회귀계수는 $\hat{\beta}^{OLS} = S^{-1}s$ 이므로, $(S+\delta I)\hat{\beta}^{RR}(\delta) = S\hat{\beta}^{OLS}$이다.
즉, 다음과 같은 관계식이 성립한다.
\[\begin{align*} \hat{\beta}^{RR}(\delta) &= (S + \delta I)^{-1}S\hat{\beta}^{OLS} = (I + \delta S^{-1})^{-1}\hat{\beta} = (I + \frac{\gamma}{1-\gamma}\tilde{e}(\gamma)S^{-1})^{-1}\hat{\beta}^{OLS} \\ \hat{\beta}^{CR}(\gamma) &= (1 + \frac{\gamma}{1-\gamma})\hat{\beta}^{RR}(\delta) = (1 + \frac{\gamma}{1-\gamma})\hat{\beta}^{RR}(\delta) = (1 + \frac{\gamma}{1-\gamma})(I + \frac{\gamma}{1-\gamma}\tilde{e}(\gamma)S^{-1})^{-1}\hat{\beta}^{OLS} \end{align*}\]shirnkage method는 불편 추정량에 스칼라 값을 곱하여 편향을 어느정도 희생시키면서, 분산을 줄여주어 MSE가 줄어드는 효과가 있었다. 하지만 MSE에서 이러한 shrinkage effect를 갖기 위하여 불편성을 억제하는것은 통계학에서 논란이 많은 주제이다. 하지만 공선성이 있는 회귀문제에서 릿지회귀는 의심의 여지 없이 좋은 성능을 보였다. 반대로 공선성이 없는 경우를 생각해보자. input vector들이 모두 orthonormal인 경우, $\mathbf{S}$는 대각 원소가 $\tilde{e}$인 대각행렬이다. 즉, $i$번째 릿지 휘귀의 회귀계수는 다음과 같다.
\[\hat{\beta}^{RR}_i(\delta) = (1 + \frac{\gamma}{1-\gamma}\tilde{e}\tilde{e}^{-1})^{-1}\hat{\beta}^{OLS} = (1-\gamma)\hat{\beta}_i^{OLS}\]$ \gamma \in [0,1) $이기에, 공선성이 없는 경우에도 shrinkage effect가 발생하였다. 이번에는 CR의 회귀계수를 계산해보면 다음과 같다.
\[\hat{\beta}^{CR}_i(\gamma) = (1 + \frac{\gamma}{1-\gamma})\hat{\beta}^{RR}_i(\delta) = \frac{1}{1-\gamma}(1-\gamma)\hat{\beta}^{OLS} = \hat{\beta}^{OLS}\]CR의 경우에서는 스칼라항 $\frac{1}{1-\gamma}$항에 의해 shirinkage effect가 발생하지 않았다. 즉, CR은 릿지의 shrinkage effect를 변형하여, 공선성이 발생한 경우에 shirinkage effect를 줄 수 있다.
릿지와 CR을 실제 모델링을 진행하여 둘을 비교해보면서 포스팅을 마치겠다. 다음 그림은 Cement heat evolution 데이터셋을 사용하여 $\delta$에 관한 cross validation을 평가지표 adjusted $R^2$ 값을 이용하여 시행한 것이다. 해당 데이터셋의 데이터마다 설명변수 $x_1, x_2,x_3,x_4$의 합은 비율이므로 100에 가까운 상수로 거의 비슷하기에, 공선성을 일으킨다.
풀모델의 경우의 adjusted $R^2$ 값은 0.974이다. 릿지 회귀는 점선으로, CR은 실선으로 표시되었다.
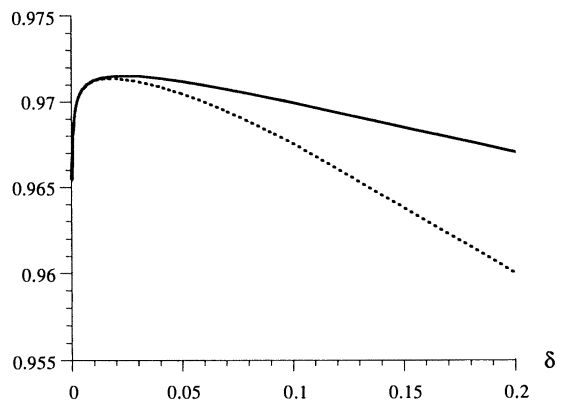
릿지 회귀와 CR 모두 작은 $\delta$에 대해 거의 같은 결과를 내지만, $\delta$가 커짐에 따라 감소하는 정도가 릿지 회귀가 더 가파르게 감소하는 것으로 보아 릿지 회귀가 파라미터에 대해 더 민감함을 알 수 있다.
