[ESL 리뷰] 교재 3장-3 Forward Stagewise Selection, Least Angle Regression

“The Elements of Statistical Learning” 교재 3장의 Shrinkage Methods중 Forward Stagewise Selection, Least Angle Regression(LAR)에 관해 정리를 해보았다.

Forward Stagewise Selection

Foward Stepwise Selection을 다룬 이전 포스팅에서는 매 iteration마다 잔차 $\mathbf{r}$을 업데이트하면서 $\mathbf{x}_j^T\mathbf{r}$가 가장 큰 $j$를 찾아서(잔차와 상관관계가 가장 높은 변수) QR분해를 이용하여 해당변수를 추가해줬었다. Forward stagewise selection은 이와 비슷하지만 변수를 한번에 추가해주는것이 아닌 점진적으로 추가하는 방법이다. 알고리즘은 아래와 같다.

Note. 3번 과정에서 $\epsilon$ 에 $\left\langle \mathbf{x}_j, \mathbf{r} \right\rangle$을 대입하면 Forward stepwise selection이다.

 

Least Angle Regression

Least Angle Regression(LARS)은 Forward Stagewise selection을 굉장히 효율적?으로 개선된 모델이다. LARS의 해를 찾는데는 p번의 iteration만으로 충분하다. 만약 $p > N-1$일 경우 $N-1$번 이후로는 잔차가 0이 됨으로 업데이트가 이루어지지 않으므로 중단한다.(1을 뺀 이유는 데이터를 표준화했기 때문)

LARS의 간단하게 예시를 들자면 다음과 같이 작동한다. 먼저, 이전 Forward stagewise selection과 같이 모든 회귀 계수를 0으로 초기화하고 잔차와 가장 상관관계가 높은 $\mathbf{x}_1$를 찾는다. 이후에는 다른 잔차와 상관관계가 높은 $\mathbf{x}_2$가 나오기 전까지 가능한 한 크게 $\mathbf{x}_1$방향으로 움직인다. 여기까지는 Forward stagewise selection와 같다. 이후 업데이트 부터가 차이가 있는데, 다음 업데이트에서 $\mathbf{x}_2$의 방향으로 업데이트를 하는것이 아닌, $\mathbf{x}_1$,$\mathbf{x}_2$ 두 벡터와 같은 각을 이루는 새로운 벡터 $\mathbf{u}_2$의 방향으로 업데이트를 진행한다.

p=2인 경우의 LARS는 다음과 같이 진행된다. $\hat{\mathbf{\mu}}_0 = \mathbf{X}\beta = 0$를 잡는다. ($\mathbf{X} = (\mathbf{x}_1, \mathbf{x_2}), \ \beta_1=\beta_2=0$) 아래 그림과 같이 $\mathbf{y}$를 $\mathbf{X}$의 열공간에 정사영시킨 벡터를 $\bar{\mathbf{y}}_2$라 하면, 잔차 $\mathbf{c}(\hat{\mathbf{\mu}})$는 다음과 같이 구할 수 있다.

\[\mathbf{c}(\hat{\mathbf{\mu}}) = \mathbf{X}^T(\mathbf{y} - \hat{\mathbf{\mu}}) = \mathbf{X}^T(\bar{\mathbf{y}}_2 - \hat{\mathbf{\mu}})\]

아래 그림에서 $\bar{\mathbf{y}}_2 - \hat{\mathbf{\mu}}$와 더 작은 각을 이루는(상관관계가 더 높은) 벡터는 $\mathbf{x}_1$이므로 (다시 말해서, $\mathbf{c}_1(\hat{\mathbf{\mu}}_0) > \mathbf{c}_2(\hat{\mathbf{\mu}}_0)$), $\mathbf{x}_1$방향으로 업데이트를 진행한다. 즉, $\hat{\mathbf{\mu}}_1 = \hat{\mathbf{\mu}}_0 + \hat{\gamma}_1 \mathbf{x}_1$이다. FS의 경우에서는 $\hat{\gamma}_1$에 $\epsilon$값을 사용하였지만, LARS는 $\bar{\mathbf{y}}_2 - \hat{\mathbf{\mu}}_1$이 $\mathbf{x}_1, \ \mathbf{x}_2$와 같은 각을 이루도록 $\hat{\gamma}_1$을 잡는다 (다시 말해서, $\hat{\gamma}_1$를 통해서 업데이트 된 예측값의 잔차를 해당 열공간에 정사영시킨 벡터와 등각을 이루도록 잡는다. 따라서 잔차와의 상관관계가 모두 같아진다.). 즉, $c_1(\hat{\mathbf{\mu}}_1) = c_2(\hat{\mathbf{\mu}}_1)$인 $\hat{\gamma}_1$를 찾는다.

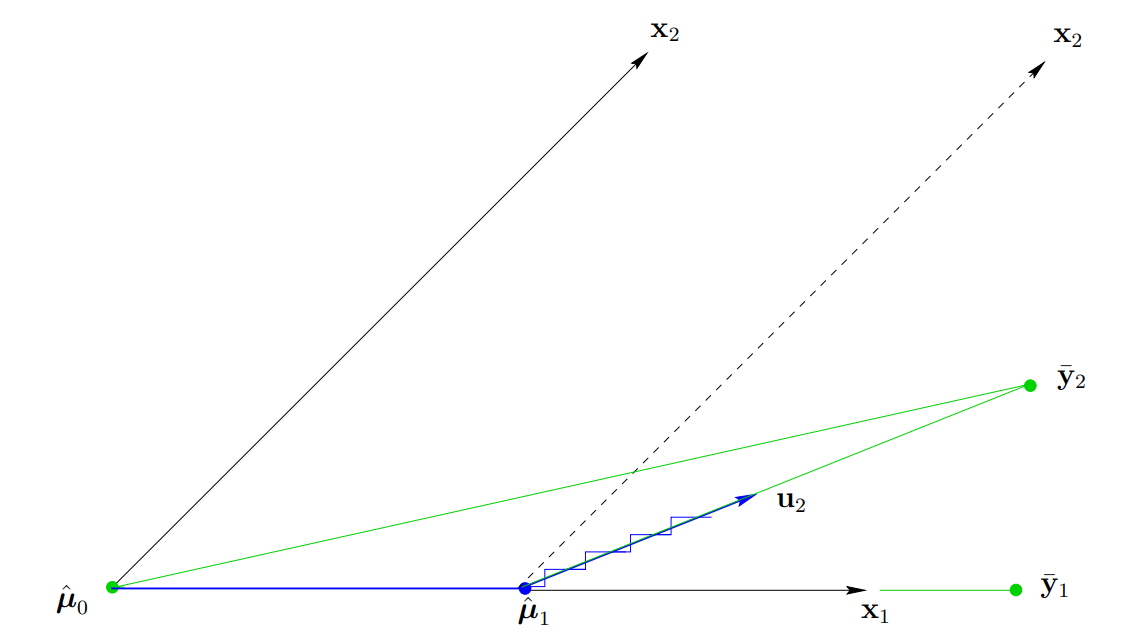
위 그림과 같이 $\mathbf{u}_2$를 $\mathbf{x}_1, \ \mathbf{x}_2$와 같은 각을 이루는 단위벡터라고 하자. LARS의 다음 스텝은 $\hat{\mathbf{\mu}}_2 = \hat{\mathbf{\mu}}_1 + \hat{\gamma}_2 \mathbf{u}_2$로, $\hat{\mathbf{\mu}}_2 = \bar{\mathbf{y}}_2$이 되도록 $\hat{\gamma}_2$을 잡는다. 만약 $p$가 2보다 클 경우에는 다음 $\mathbf{x}_3$와 같은 각을 이루도록, $\hat{\gamma}_2$를 더 작게 잡아 방향을 바꾼다. ($\hat{\mathbf{\mu}}_2 = \bar{\mathbf{y}}_2$이 되도록 잡은 $\hat{\gamma}_2$에 대한 잔차는 현재 컬럼벡터들과 수직으로 내적값이 0이다. 즉, $p>2$인 경우 다른 컬럼이 존재하여 이와의 내적값이 0보다 클 것이기에 이전에 방향이 바뀌게 된다.)

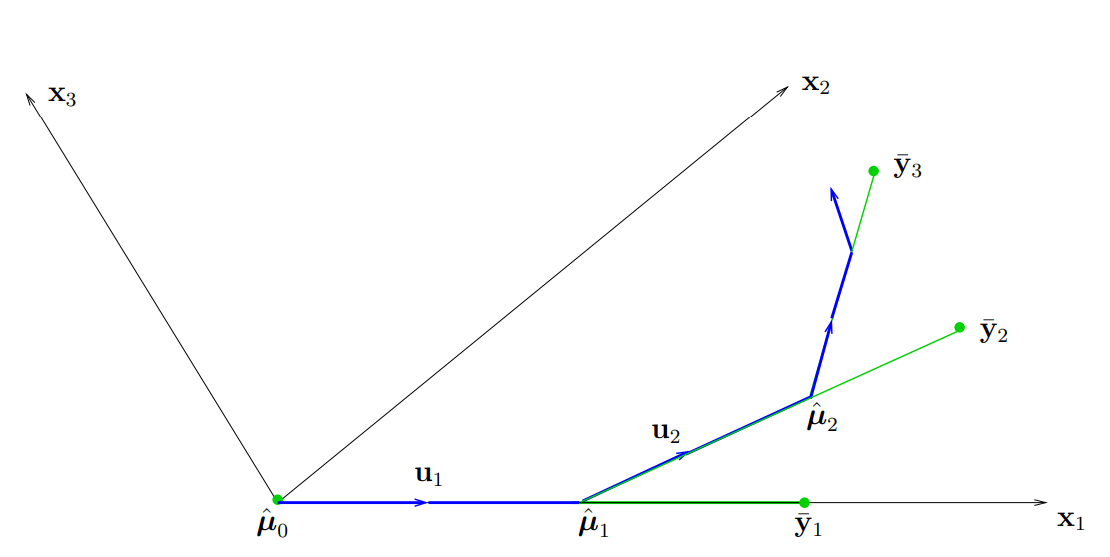
(위 그림을 보면, $k$번째 스탭에서 LARS의 estimator \(\hat{\mu}_k\)는 이전 스텝의 estimator인 \(\hat{\mu}_{k-1}\)과 현재 OLS estimator인 \(\bar{\mathbf{y}}_k\)의 직선상에 놓여있음을 확인할 수 있다. 이에 대해서는 밑에서 다시 다룰 예정이다.)

LARS의 작동과정은 알아봤으니 이제 $\hat{\gamma}_1,\hat{\gamma}_2,… $들을 구하는 방법을 알아보자. 먼저 $\mathbf{X}$의 열벡터는 모두 선형독립이라고 가정하자. $\mathcal{A}$를 현재 선택된 변수들의 인덱스를 모아놓은 집합이라고 하고, 다음과 같이 정의해보자.

\[\begin{align*} \mathbf{X}_{\mathcal{A}} &= (..., s_j\mathbf{x}_j,...)_{j\in \mathcal{A}}, \ s_j = sign(\left\langle \mathbf{x}_j, \mathbf{y}-\hat{\mathbf{\mu}}_{\mathcal{A}} \right\rangle) \\ \mathbf{\mathcal{G}}_{\mathcal{A}} &= \mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}} \\ \mathbf{A}_{\mathcal{A}} &= (1_{\mathcal{A}}^T \mathbf{\mathcal{G}}^{-1} 1_{\mathcal{A}})^{-\frac{1}{2}} \in \mathbb{R} \ \text{where} \ \ 1_{\mathcal{A}} \in \mathbb{R}^{|\mathcal{A}|} \text{is a vector of 1's} \end{align*}\]

이렇게 정의하고 나면, $\mathbf{X}_{\mathcal{A}}$내의 열벡터들과 같은 각을 이루는 벡터 $\mathbf{u}$를 다음과 같이 잡을 수 있다.

\[\mathbf{u}_{\mathcal{A}} = \mathbf{X}_{\mathcal{A}} w_{\mathcal{A}}, \ \text{ where} \ w_{\mathcal{A}} = \mathbf{A}_{\mathcal{A}}\mathbf{\mathcal{G}}_{\mathcal{A}}^{-1}1_{\mathcal{A}}\]

다음 내적을 통해 $\mathbf{u}_{\mathcal{A}}$가 같은 각을 이루는지 확인할 수 있다.

\[\mathbf{X}_{\mathcal{A}}^T\mathbf{u}_{\mathcal{A}} = \mathbf{X}_{\mathcal{A}}^T(\mathbf{X}_{\mathcal{A}}w_{\mathcal{A}}) = \mathbf{A}_{\mathcal{A}}\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}}\mathbf{\mathcal{G}}_{\mathcal{A}}^{-1}1_{\mathcal{A}} = \mathbf{A}_{\mathcal{A}}1_{\mathcal{A}} \ \text{and} \ \ \|\mathbf{u}_{\mathcal{A}}\|^2=1\]

 

LARS algorithm: LARS의 대략적인 작동 과정은 다음과 같다.

시작은 Forward stagewise selection과 같이 초기 예측값 $\hat{\mu}_0 = 0$으로 초기화 한다. 다음으로, 현재 예측값인 \(\hat{\mu}_{\mathcal{A}}\) 에 대한 잔차를 구하여 모든 피쳐벡터들과 상관관계를 구한다. 즉, 다음을 계산한다.

\[\hat{\mathbf{c}} = \mathbf{X}^T(\mathbf{y}-\hat{\mathbf{\mu}}_{\mathcal{A}})\]

구한 상관관계를 바탕으로 active set $\mathcal{A}$와 $\mathbf{X}_{\mathcal{A}}$를 구하기 위한 sign 함수를 다음과 같이 구한다.

\[\begin{align*} \mathcal{A} &= \{j: | \mathbf{c}_j | = \hat{C} \} \ \text{where} \ \hat{C} = max_j | \mathbf{c}_j | \\ s_j &= sign(\hat{\mathbf{c}}_j) \ \text{for} \ j \in \mathcal{A} \end{align*}\]

$\hat{\gamma}$를 구하기 위해 모든 피쳐들에 대해 다음과 같은 내적을 계산하여 업데이트를 진행한다.

\[\begin{align*} \mathbf{a} &= \mathbf{X}^T\mathbf{u}_{\mathcal{A}} \\ \hat{\gamma} &= min^+ \{ \frac{\hat{C} - \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} - a_j}, \frac{\hat{C} + \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} + a_j} \} \\ \beta_{\mathcal{A}_j} &\leftarrow \beta_{\mathcal{A}_j} + \hat{\gamma}w_{\mathcal{A}_j} \\ \hat{\mu}_{\mathcal{A}} &\leftarrow \hat{\mu}_{\mathcal{A}} + \hat{\gamma}\mathbf{u}_{\mathcal{A}} \ (\mathbf{r} \leftarrow \mathbf{r} - \hat{\gamma}\mathbf{u}_{\mathcal{A}}) \end{align*}\]

 

Equiangular vector 유도 과정

위 식에서 $\mathbf{u}_{\mathcal{A}}$가 어떻게 유도되었는지는 다음과 같다.

먼저 $\mathbf{X}_{\mathcal{A}}$내의 모든 열벡터들과 같은 각을 이루므로 내적값이 모두 같아야 한다. 식으로 나타내면 다음과 같다.

\[\mathbf{X}_{\mathcal{A}}^T\mathbf{u}_{\mathcal{A}} = \alpha 1_{\mathcal{A}}, \ \alpha \ \text{is constant} \ \text{and} \ \| \mathbf{u}_{\mathcal{A}} \|^2 = 1\]

계산상의 편의를 위해 $\alpha$를 1일 때 위를 만족하는 벡터 $v_{\mathcal{A}}$를 찾아 이에 대한 단위벡터를 구해$\mathbf{u}_{\mathcal{A}}$를 유도해보자. 이는 항등행렬을 이용하여 풀 수 있다.

\[\begin{align*} \mathbf{I}_{\mathcal{A}} 1_{\mathcal{A}} &= 1_{\mathcal{A}} \ (\mathbf{I}_{\mathcal{A}} \in \mathbb{R}^{|\mathcal{A}| \times |\mathcal{A}|} \ \text{is identity matrix}) \\ \mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} &= 1_{\mathcal{A}} \\ \mathbf{X}_{\mathcal{A}}^T(\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}}) &= 1_{\mathcal{A}} \\ \mathbf{X}_{\mathcal{A}}^Tv_{\mathcal{A}} &= 1_{\mathcal{A}} \end{align*}\]

따라서 $v_{\mathcal{A}}$의 단위벡터를 구하면 된다.

\[\begin{align*} \mathbf{u}_{\mathcal{A}} &= \frac{v_{\mathcal{A}}}{\|v_{\mathcal{A}}\|} \\ &= \frac{1}{\| \mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}}\|} \mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} \end{align*}\]

또한 \(\| \mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} \|\) 은 다음과 같이 구할 수 있다.

\[\begin{align*} (\| \mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} \|^2)^{\frac{1}{2}} &= (\left\langle\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}}, \mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} \right\rangle)^{\frac{1}{2}} \\ &= ((\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}})^T\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}})^{\frac{1}{2}} \\ &= (1_{\mathcal{A}}^T (\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1} 1_{\mathcal{A}})^{\frac{1}{2}} \end{align*}\]

따라서 $\mathbf{u}_{\mathcal{A}}$는 다음과 같다.

\[\begin{align*} \mathbf{u}_{\mathcal{A}} &= (1_{\mathcal{A}}^T (\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1} 1_{\mathcal{A}})^{-\frac{1}{2}}\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}1_{\mathcal{A}} \\ &= \mathbf{A}_{\mathcal{A}}\mathbf{X}_{\mathcal{A}}\mathbf{\mathcal{G}}^{-1}_{\mathcal{A}} 1_{\mathcal{A}} \\ &= \mathbf{X}_{\mathcal{A}}\mathbf{A}_{\mathcal{A}}\mathbf{\mathcal{G}}^{-1}_{\mathcal{A}} 1_{\mathcal{A}} (\because \mathbf{A}_{\mathcal{A}} \in \mathbb{R}) \\ &= \mathbf{X}_{\mathcal{A}}w_{\mathcal{A}} \end{align*}\]

 

Note. $\mathbf{u}_{\mathcal{A}}$는 즉, 현재 선택된 컬럼들을 이용한 잔차를 현재 열공간에 정사영 시킨 벡터와 같은 방향을 이룬다.

즉, 현재 hat matrix를 $\mathbf{H}_{\mathcal{A}}$라 할 때 \(\mathbf{u}_{\mathcal{A}} = \lambda \mathbf{H}_{\mathcal{A}}(\mathbf{y} - \hat{\mu}_{\mathcal{A}}) = \lambda\mathbf{X}_{\mathcal{A}}(\mathbf{X}_{\mathcal{A}}^T\mathbf{X}_{\mathcal{A}})^{-1}\mathbf{X}_{\mathcal{A}}^T(\mathbf{y} - \hat{\mu}_{\mathcal{A}})\) ($\lambda$는 상수) 이다.

 

$\hat{\gamma}$ 유도 과정

다시 본론으로 넘어가서 현재 $\hat{\mathbf{\mu}}_{\mathcal{A}}$에서 $\hat{\gamma}$를 찾아보자. 현재 단계에서 벡터마다 상관관계는 \(c_j = \mathbf{x}_j^T(\mathbf{y}-\hat{\mathbf{\mu}}_{\mathcal{A}})\) 이다. 또한 현재 뽑힌 변수들의 인덱스 집합 $\mathcal{A}$은 다음과 같다.

\[\mathcal{A} = \{j: | \mathbf{c}_j | = \hat{C} \} \ \text{where} \ \hat{C} = max_j | \mathbf{c}_j |\]

$j \in \mathcal{A}$에 대해 $s_j = sign(\hat{\mathbf{c}}_j)$라 하고, \(\mathbf{a} = \mathbf{X}^T\mathbf{u}_{\mathcal{A}}\) 라 하자(만약 $j \in \mathcal{A}$라면 \(a_j = \mathbf{A}_{\mathcal{A}}\)). 이제 다음 업데이트할 $\hat{\mathbf{\mu}}$와 상관관계를 \(\gamma (\gamma > 0)\)에 대한 함수로 정의해보자.

\[\begin{align*} \mathbf{\mu}(\gamma) &= \hat{\mathbf{\mu}}_{\mathcal{A}} + \gamma \mathbf{u}_{\mathcal{A}}, \\ c_j(\gamma) &= \mathbf{x}_j^T(\mathbf{y} - \mathbf{\mu}(\gamma)) = \hat{c}_j - \gamma a_j \end{align*}\]

만약 $j \in \mathcal{A}$라면, \(|\mathbf{c}_j(\gamma )| = | \hat{\mathbf{c}}_j - \gamma a_j | = | \hat{C} - \gamma A_{\mathcal{A}}|\) 이다.

$\mathbf{u}_{\mathcal{A}}$가 현재 잔차를 열공간에 정사영시킨 벡터의 단위벡터이므로 다음이 성립한다.

\[\mathbf{A}_{\mathcal{A}} = \mathbf{x}_j^T \mathbf{u}_{\mathcal{A}}, \ \hat{C} = \mathbf{x}_j^T (\mathbf{y} - \hat{\mathbf{\mu}}_{\mathcal{A}}) = \mathbf{x}_j ^T(\lambda\mathbf{u}_A + \mathbf{v}) \ \text{where} \ \mathbf{x}_j \perp \mathbf{v}\]

즉 두벡터는 같은 방향을 가지고 있고, 업데이트 과정에서 현재 active set에 포함되지 않는 다른 컬럼이 존재한다면 $\gamma$는 항상 $\gamma \mathbf{A}_{\mathcal{A}}$가 $\hat{C}$보다 작거나 같도록 업데이트가 진행된다. 만약 같다면 잔차와의 내적값이 0이 된다. 따라서,

\[|c _j(\gamma )| = \hat{C} - \gamma \mathbf{A}_{\mathcal{A}}\]

이다.

Note. (OLS와 LARS의 관계) LARS알고리즘이 $k-1$번째 단계까지 업데이트가 진행되었고 현재 $k$번째 단계라고 가정해보자. $\mathbf{y}$를 $\mathbf{X}_k$의 열공간에 사영시킨 벡터를 $\bar{\mathbf{y}}_k$라고 한다면 다음이 성립한다.

\[\begin{align*} \bar{\mathbf{y}}_k &= \hat{\mu}_{k-1} + \mathbf{X}_k(\mathbf{X}_k^T\mathbf{X}_k)^{-1}\mathbf{X}_k^T(\mathbf{y} - \hat{\mu}_{k-1}) \\ &= \hat{\mu}_{k-1} + \mathbf{X}_k(\mathbf{X}_k^T\mathbf{X}_k)^{-1}\hat{C}_k1_k \\ &= \hat{\mu}_{k-1} + \hat{C}_k \mathbf{X}_k\mathcal{G}_k^{-1}1_k = \hat{\mu}_{k-1} + \frac{\hat{C}_k}{\mathbf{A}_k}\mathbf{u}_{k} \end{align*}\]

또한 $\bar{\gamma}_k = \frac{\hat{C}_k}{\mathbf{A}_k} $라고 정의하면 다음 관계식이 성립한다.

\[\hat{\mu}_{k} - \hat{\mu}_{k-1} = \frac{\hat{\gamma}_k}{\bar{\gamma}_k}(\bar{\mathbf{y}}_k - \hat{\mu}_{k-1})\]

마찬가지로 \(\hat{\gamma}_k\)는 \(\bar{\gamma}_k\)를 넘을 수 없다. 즉, LARS의 추정량인 \(\hat{\mu}_k\)는 이전 스텝의 \(\hat{\mu}_{k-1}\)와 현재 스텝의 OLS 추정량인 \(\bar{\mathbf{y}}_k\)가 이루는 직선 상에 있으며 \(\hat{\mu}_{k-1}\)에 더 가까이 있다. LARS의 추정량은 OLS의 추정량을 넘을 수 없다.

 

다시 유도과정으로 넘어와서, 새로운 $j \in \mathcal{A}^C$에 대해서도 같은 각을 이루도록 $\gamma$를 잡아야 하므로$\mathbf{c}_j(\gamma )$가 양수면,

\[\begin{align*} \mathbf{c}_j(\gamma ) &= \hat{\mathbf{c}}_j - \gamma a_j = \hat{C} - \gamma \mathbf{A}_{\mathcal{A}} \\ \gamma &= \frac{\hat{C} - \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} - a_j} \end{align*}\]

반대로, $\mathbf{c}_j(\gamma )$가 음수면,

\[\begin{align*} -\mathbf{c}_j(\gamma ) &= -\hat{\mathbf{c}}_j + \gamma a_j = \hat{C} - \gamma \mathbf{A}_{\mathcal{A}} \\ \gamma &= \frac{\hat{C} + \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} + a_j} \end{align*}\]

이다. 따라서 $\hat{\gamma}$는 위 두 값중 작은 값을 취한다. 즉,

\[\hat{\gamma} = min^+ \{ \frac{\hat{C} - \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} - a_j}, \frac{\hat{C} + \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} + a_j} \}\]

이고 다음과 같이 업데이트를 진행한다. ($min+$는 두 값 중 양수 값만 받아 최솟값을 구함.) 즉 잔차와의 상관관계 $\hat{C}_k$ 는 $k$가 증가할때마다 감소함을 알 수 있다.

\[\hat{\mathbf{\mu}}^+ = \hat{\mathbf{\mu}} + \hat{\gamma}\mathbf{u}_{\mathcal{A}}\]

마지막 p번째 단계에서, 즉 모든 변수가 $\mathcal{A}_p$에 포함된다면 $j \in \mathcal{A}_p^C$가 없기 때문에 위 $\hat{\gamma}$를 구할 수 없다. 이 때에는 $\hat{\mu}_p$를 $\mathbf{y}$를 현재 $\mathbf{X}$의 열공간에 정사영 시킨 벡터 $\bar{\mathcal{y}}_p$가 되도록 업데이트를 진행한다. 즉, \(\hat{C}_p = \hat{\gamma}_p \mathbf{A}_{\mathcal{A}_p}\) 이 되어야 하므로 \(\hat{\gamma}_p = \frac{\hat{C}_p}{\mathbf{A}_{\mathcal{A}_p}}\) 가 된다.

Summary

LARS의 작동과정을 간단히 나타내면 다음과 같다.

1. 잔차 $\mathbf{r}$ 을 $\mathbf{y}$로 ($\hat{\mu}_0 = 0$), $\beta_1 = … = \beta_p = 0$으로 초기화하고 $\mathbf{X}$를 표준화한다.

2. $\mathbf{r}$와 상관관계가 가장 높은 변수 $\mathbf{x}_j$를 선택한다.

3. 현재 단계에서 \(\mathcal{A}, \mathbf{X}_{\mathcal{A}}, \mathbf{\mathcal{G}}_{\mathcal{A}}, \mathbf{A}_{\mathcal{A}}\)를 계산한다.

4. $\mathcal{A}$에 모든 벡터가 포함되지 않았다면, \(\mathbf{u}_{\mathcal{A}}, \ \hat{\gamma} = min^+ \{ \frac{\hat{C} - \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} - a_j}, \frac{\hat{C} + \hat{\mathbf{c}}_j}{\mathbf{A}_{\mathcal{A}} + a_j} \}\) 를 계산하여 \(\beta_{\mathcal{A}_j} \leftarrow \beta_{\mathcal{A}_j} + \hat{\gamma} w_{\mathcal{A}_j} , \ \hat{\mu} \leftarrow \hat{\mu} + \hat{\gamma} \mathbf{u}_{\mathcal{A}}\)로 업데이트를 진행한다. 만약 $N-1$번 이상으로 진행되면 업데이트가 이뤄지지 않으므로 종료한다.

5. $p$ 번째 iteration, 즉 $\mathcal{A}$에 모든 변수가 포함되었다면, \(\hat{\gamma}_p = \frac{\hat{C}_p}{\mathbf{A}_{\mathcal{A}_p}}\)를 계산하여, \(\beta_p \leftarrow \beta_p + \hat{\gamma} w_{\mathcal{A}_j} , \ \hat{\mu} \leftarrow \hat{\mu} + \hat{\gamma} \mathbf{u}_{\mathcal{A}}\)로 업데이트를 진행하여 종료한다.

다음 포스팅에서는 Forward stagewise selection, LARS, LASSO의 유사한 점을 비교해볼 것이다.