[ESL 리뷰] 교재 3장-2 Shrinkage Methods(Ridge, Lasso)

“The Elements of Statistical Learning” 교재 3장의 Shrinkage Methods에 관한 내용을 정리해보았다. 앞서 subset selection을 통해 모델의 해석력과 더 나은 prediction error를 가질수 있음을 알 수 있었다. 하지만 subset selection은 변수를 보존하거나 제거하는 이산적인 과정이기에 높은 분산을 가질 수 있고, 따라서 full 모델의 prediction error를 줄이지 못할 수도 있다. 다음으로 배워볼 shrinkage method들은 더 연속적이기에 높은 분산을 가지는 것을 피할 수 있다.

Ridge Regression

Ridge regression은 회귀 계수의 크기만큼의 패널티를 부과하는 방법이다. RSS를 사용하여 나타내면 다음과 같다.

\[\hat{\beta}^{ridge} = argmin_{\beta} \sum_{i=1}^N(y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 + \lambda \sum_{j=1}^p\beta_j^2\]

$\lambda \geq 0$는 complexity parameter로 패널티의 정도를 조절한다. RSS를 통한 릿지는 이후에 신경망을 다룰 때 weight decay로 다시 활용된다. 위 릿지 문제는 라그랑주 승수법을 활용하면 아래의 문제를 푸는 것과 동치이다.

\[\hat{\beta}^{ridge} = argmin_{\beta} \sum_{i=1}^N(y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 \ \text{subject to } \sum_{j=1}^p \beta_j^2 \leq t\]

즉, 회귀 계수를 상수 $t$보다 작거나 같다는 제약조건을 걸어 RSS를 푸는 문제이므로 독립변수들간의 스케일링이 먼저 이뤄져야 한다. 따라서 다음부터 나올 input variable들은 아래와 같은 표준화가 이뤄졌다고 가정하고 논의를 이어나간다.

\[\frac{1}{N}\sum_{i=1}^N x_{ij} = 0, \ \frac{1}{N}\sum_{i=1}^N x_{ij}^2 = 1 \ \text{for all} \ j=1,...,p\]

주목해야할 점은 절편인 $\beta_0$에 대한 패널티를 부과하지 않았다는 점인데, 이는 스케일링에 영향을 받기 때문이다. 다음 식은 위의 릿지와 같은 해를 갖는다.

\[\begin{align*} \hat{\beta}^{c} &= argmin_{\beta^c} \left \{ \sum_{i=1}^N \left[ y_i - \beta_0^c - \sum_{j=1}^p (x_{ij} - \bar{x}_j)\beta_j^c \right]^2 + \lambda \sum_{j=1}^p{\beta_j^c}^2 \right \} \\ \hat{\beta}^{ridge} &= argmin_{\beta^c} \left \{ \sum_{i=1}^N \left[ y_i - \beta_0 - \sum_{j=1}^p \bar{x}_{j}\beta_j - \sum_{j=1}^p(x_{ij} - \bar{x}_j)\beta_j \right]^2 + \lambda \sum_{j=1}^p{\beta_j}^2 \right \} \\ &\text{ where } \beta_0^c = \beta_0 + \sum_{j=1}^p \bar{x}_j\beta_j, \ \beta_j^c = \beta_j \text{ for } j=1,...,p \end{align*}\]

즉 \(\beta_0\)에 대해서는 스케일링 이후에 값이 이전과 같지 않는 \(X\)의 영향을 받기에 패널티를 부과하지 않는다.

릿지 회귀를 행렬표현으로 바꿔 해를 구하면 다음과 같다. (\(\mathbf{X}\)는 \(p\)개의 컬럼을 갖는다는점에 유의하자.)

\[\begin{align*} RSS = (\mathbf{y} - \mathbf{X}\beta)^T(\mathbf{y} - \mathbf{X}\beta) + \lambda \beta^T\beta, \\ \frac{\partial RSS}{\partial \beta} = -2\mathbf{X}^T(\mathbf{y} - \mathbf{X}\beta) + 2\lambda\beta = 0, \\ \end{align*}\]

따라서 \(\hat{\beta}^{ridge} = (\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^T\mathbf{y}\) 이다. 이것이 릿지 회귀를 제안하였을 때 처음 나온 식이다. 예를 들어 $p > N$일 경우, $\mathbf{X}^T\mathbf{X}$는 full-rank가 아니기에, 역행렬을 가지지 않는다. 때문에 각 대각원소에 $\lambda$를 더해 역행렬을 구할 수 있도록 처음 제안되었었다.(Hoerl and Kennard, 1970).

 

Ridge regression as MAP(Maximum A Posteriori) Estimation

다음과 같이 $y_i \sim \mathcal{N}(\beta_0 + x_i^T\beta, \sigma^2)$이고 회귀 계수 $\beta_j \sim \mathcal{N}(0,\tau^2)$ 를 따른다고 가정해보자.(각 $y_i, \ \beta_j$들은 독립이다.) 다시 말해서, $\beta \sim \mathcal{N}(0,\tau \mathbf{I}), \ \mathbf{y} \sim \mathcal{N}(\mathbf{X}\beta, \sigma^2 \mathbf{I})$이므로, 베이즈 정리를 이용하면

\[\begin{align*} argmax_{\beta} \log p(\beta | \mathbf{y}) &= argmax_{\beta} \log p(\mathbf{y} | \beta)p(\beta) \\ &= argmin_{\beta} \frac{1}{2}(\frac{(\mathbf{y} - \mathbf{X}\beta)^T(\mathbf{y} - \mathbf{X}\beta)}{\sigma^2} + \frac{\beta^T\beta}{\tau^2}) \\ &= argmin_{\beta}(\mathbf{y} - \mathbf{X}\beta)^T(\mathbf{y} - \mathbf{X}\beta) + \frac{\sigma^2}{\tau^2}\beta^T\beta \end{align*}\]

이다. 즉 complex paramter $\lambda$를 $\frac{\sigma^2}{\tau^2}$로 넣으면 완전히 같은 식이다.

 

Ridge regression with SVD(+ PCA)

$\mathbf{X} \in \mathbb{R}^{N \times p}$를 특잇값 분해를 통해 다음과 같이 나타낼 수 있다.

\[\mathbf{X} = \mathbf{U} \mathbf{D} \mathbf{V}^T\]

$\mathbf{U} \in \mathbb{R}^{N \times p}, \ \mathbf{V} \in \mathbb{R}^{p \times p}$는 직교행렬로 각각 $\mathbf{X}$의 열공간과 행공간를 span하고, $\mathbf{D} \in \mathbb{R}^{p \times p}$는 대각원소가 $\mathbf{X}$의 특잇값 $d_1 \geq d_2 \geq … \geq d_p \geq 0$ ($\mathbf{X}^T\mathbf{X}$의 고윳값의 제곱근, 참고로 $\mathbf{X}$의 표본 공분산 행렬은 $\mathbf{X}^T\mathbf{X}/N$이다.)인 대각행렬이다.

특잇값 분해를 통해 최소제곱해를 나타내면 다음과 같다.

\[\begin{align*} \mathbf{X}\hat{\beta}^{ls} &= \mathbf{X}(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{U}^T\mathbf{y} \\ &= \sum_{j=1}^p \mathbf{u}_j\mathbf{u}_j^T\mathbf{y} \ \text{where the} \ \mathbf{u}_j \ \text{are the columns of} \ \mathbf{U} \end{align*}\]

$\mathbf{U}$의 컬럼벡터들은 $\mathbf{X}$의 열공간의 정규직교 기저이므로, $\mathbf{y}$를 $\mathbf{X}$의 열공간에 정사영시킨 $\hat{\mathbf{y}}$을 직교기저 $\mathbf{u}_1, …, \mathbf{u}_p$와 스칼라 $\left\langle \mathbf{u}_j, \mathbf{y} \right\rangle$의 선형결합을 통해 표현한 것이다. 마찬가지로 릿지회귀의 해를 나타내면 다음과 같다.

\[\begin{align*} \mathbf{X}\hat{\beta}^{ridge} &= \mathbf{X}(\mathbf{X}^T\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^T\mathbf{y} \\ &= \mathbf{U}\mathbf{D}(\mathbf{D}^2 + \lambda \mathbf{I})^{-1}\mathbf{D}\mathbf{U}^T\mathbf{y} \\ &= \sum_{j=1}^p \mathbf{u}_j \frac{d_j^2}{d_j^2 + \lambda} \mathbf{u}_j^T\mathbf{y} \end{align*}\]

즉, $\frac{d_j^2}{d_j^2 + \lambda}$에 의해 $\hat{\mathbf{y}}$에 대한 $\mathbf{u}_j$의 영향력이 줄어든다. $d_j$가 크면 1에 가까워지고, 매우 작으면 0에 가까워져 해당 변수에 대한 영향력이 줄어든다. 여기서 $d_j$가 작은 값을 갖는 것은 무엇을 의미하는지 더 알아보자.

$\mathbf{X}^T\mathbf{X} = \mathbf{V}\mathbf{D}^2\mathbf{V}$로, 이는 $\mathbf{X}^T\mathbf{X}$의 교윳값 분해로도 볼 수 있다. 고유벡터 $v_j$ ($\mathbf{V}$의 $j$번째 컬럼벡터)는 $\mathbf{X}$의 주성분 방향(principal component direction)이라고 한다. first principal component $v_1$에 대해 $\mathbf{z}_1 = \mathbf{X}v_1$는 $\mathbf{X}$의 열공간의 선형결합 중 가장 큰 표본 분산을 가지며, 다음과 같이 표현할 수 있다.

\[\begin{align*} Var(\mathbf{z}_1) &= Var(\mathbf{X}v_1) = \frac{1}{N}\sum_{i=1}^{N}(\mathbf{x}_i^Tv_1)^2 \\ &= v_1^T\frac{1}{N}\sum_{i=1}^{N}\mathbf{x}_i\mathbf{x}_i^Tv_1 = v_1^T\frac{1}{N}\mathbf{X}^T\mathbf{X}v_1 = \frac{1}{N}v_1^Td_1^2v_1 \\ &= \frac{d_1^2}{N}\|v_1\|^2 = \frac{d_1^2}{N} \end{align*}\]

또한 $\mathbf{X}\mathbf{V} = \mathbf{U}\mathbf{D}$이므로, $\mathbf{z_1} = \mathbf{X}v_1 = \mathbf{u}_1d_1$이다. 즉 작은 $d_j$는 $\mathbf{X}$의 작은 표본 분산을 가지는 방향이고, 릿지는 이러한 방향들의 영향을 줄여준다.

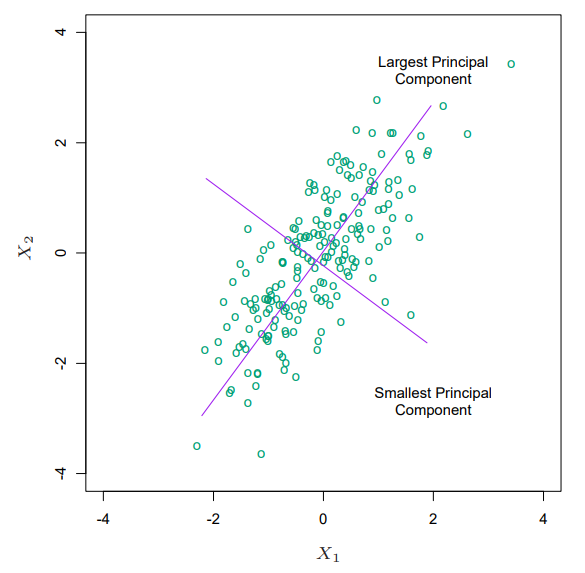
릿지 회귀는 위의 그림에서 $\mathbf{y}$를 Principal component에 정사영시키면서, 정사영된 input data들의 표본 분산이 작은 주성분인 Smallest Principal Component의 영향을 더 줄여준다. 각 주성분들은 모두 여러 변수의 선형결합으로 이뤄져 있으므로 한 축이 0이 된다해도 제거되는 변수는 없음을 알 수 있다. 그렇기에 릿지회귀에서는 effective degrees of freedom을 정의하여 연속된 버전으로 어느정도의 파라미터를 사용했는지를 파악한다. effective degrees of freedom는 다음과 같이 정의한다.

\[\begin{align*} \text{df}(\lambda) &= tr(H_{\lambda}) \\ &= tr[\mathbf{X}(\mathbf{X^T}\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^T] \\ &= \sum_{j=1}^p \frac{d_j^2}{d_j^2 + \lambda} \end{align*}\]

$\lambda$가 0일 때 df($\lambda$)는 p로 모든 변수를 사용함을 알 수 있고, $\lambda$가 매우 큰 값을 가지면 0으로 수렴하여 어떠한 변수도 사용하지 않음을 알 수 있다. 일반적으로 최적의 $\lambda$를 찾기 위해서는 cross-validation를 이용해 가장 작은 test error를 갖는 $\lambda$를 찾는다.

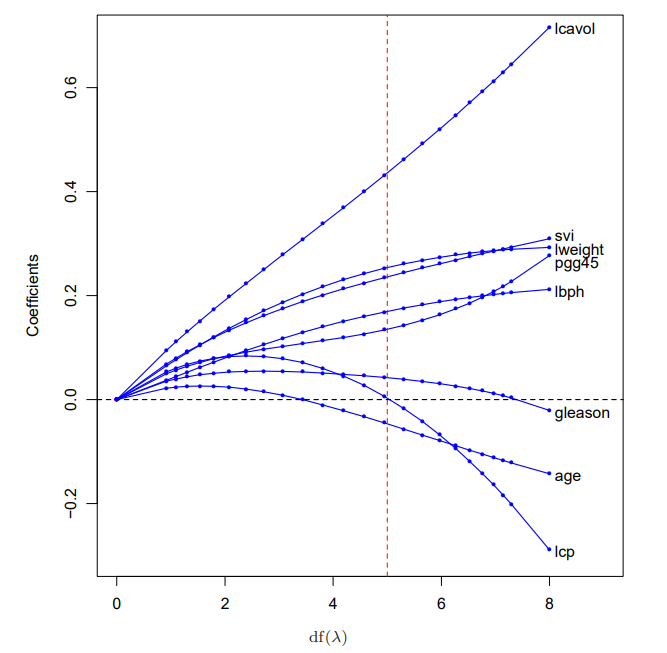
다음 그래프는 prostate cancer example 데이터셋을 이용해 릿지회귀를 나타낸 것이다. 빨간 점선으로 칠해진 수직선은 cross-validation을 통해 test error가 가장 낮은 $\lambda$ (df=5.0)를 찾은것이다.

 

The Lasso

라쏘에 관련해서는 이후 포스팅에서 다룰 내용이 많으므로 간략하게만 소개한다. 라쏘는 릿지와 유사한 shrinkage method로 다음과 같이 정의한다.

\[\hat{\beta}^{lasso} = argmin_{\beta} \sum_{i=1}^N(y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 \ \text{subject to } \sum_{j=1}^p | \beta_j | \leq t\]

마찬가지로 라그랑주 승수법을 이용하여 문제를 변환하면 다음과 같다.

\[\hat{\beta}^{lasso} = argmin_{\beta} \{ \frac{1}{2}\sum_{i=1}^N(y_i - \beta_0 - \sum_{j=1}^p x_{ij}\beta_j)^2 +\lambda \sum_{j=1}^p | \beta_j | \}\]

두번째 항때문에 릿지에서 처럼 미분을 통해 최적해를 구할 수 없다. 이후에 포스팅할 LAR 알고리즘을 활용하여 구현이 가능하다. 다음 그림에 나오는 라쏘 제약조건의 특성때문에 매우 작은 $t$를 잡으면, 몇몇의 회귀계수가 0이 될 수 있기에 라쏘를 일종의 continuous subset selection로 볼 수 있다.

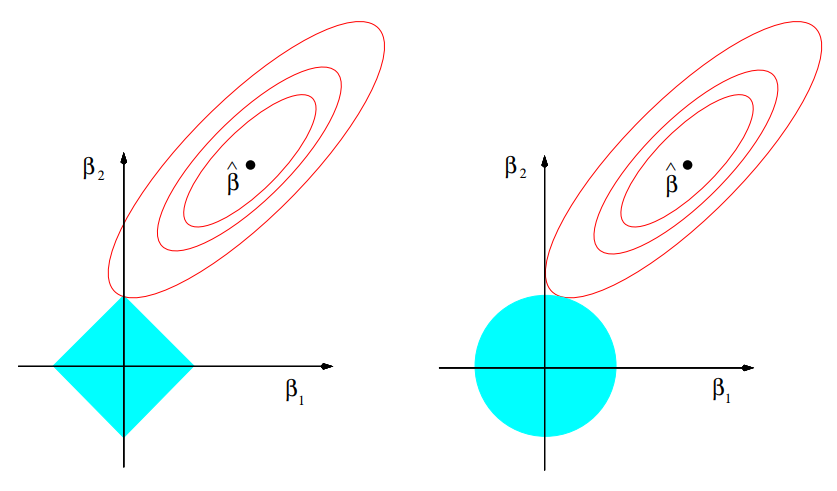
위 두 그램에서 타원은 RSS를 나타내고 색칠된 영역은 왼쪽은 라쏘의 제약조건, 오른쪽은 릿지의 제약조건을 나타낸다. 릿지와 라쏘 모두 처음으로 만나는 부분이 최적의 계수이다. 릿지의 경우 영역이 모두 미분가능하므로 매끄럽기에 위 그림에서 $\beta_1$이 0인 부분에서 만날 확률이 0이지만, 라쏘의 경우 미분 불가능한 점들이 있기에 위 그림처럼 $\beta_1$가 0이 될 수 있다.

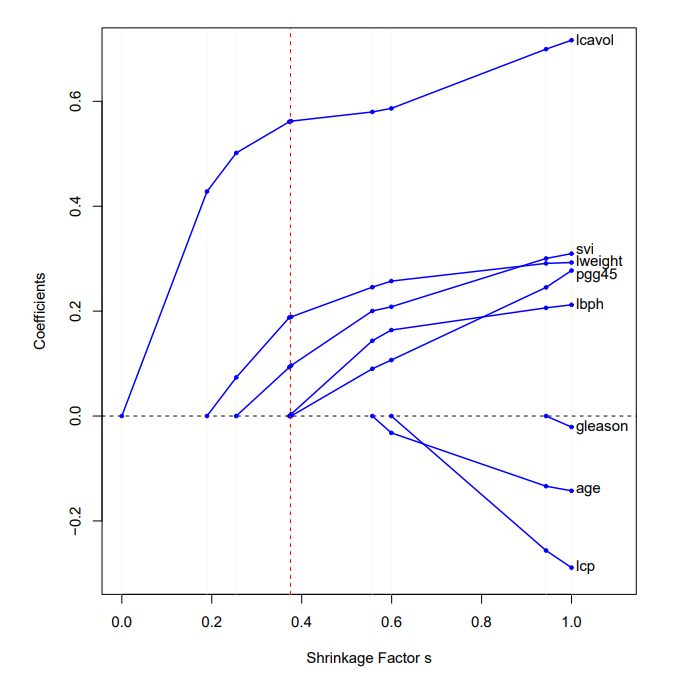
다음 그래프는 prostate cancer example 데이터셋을 이용해 라쏘를 나타낸 것이다. x축의 Shirnkage Factor인 $s$는 $\frac{t}{\sum_{j=1}^p | \hat{\beta_j} |}$이다. 빨간 점선으로 칠해진 직선은 릿지와 마찬가지로 cross-validation을 통해 찾은 최적의 $s$(=0.36)이다.