[ESL 리뷰] 교재 3장-1 Computing OLS Coefficients Using QR Decomposition, Subset selection

“The Elements of Statistical Learning” 교재 3장의 subset selection 파트의 앞부분에 관한 내용을 정리해보았다.

Multiple Regression from Univariate Regression

선형모델 $f(X) = \beta_0 + \sum_{j=1}^p X_j \beta_j \ (X^T=(X_1,…,X_p) \in \mathbb{R}^{p}, \ Y \in \mathbb{R} )$을 가정해보자. 절편이 없는 단순회귀 모델에서의 최소제곱 추정량 $\hat{\beta}$은 $\frac{\sum_1^N x_iy_i}{\sum_1^N x_i^2} = \frac{<\mathbf{x},\mathbf{y}>}{<\mathbf{x},\mathbf{x}>}$이고 잔차 $\mathbf{r}$은 $\mathbf{y}-\mathbf{x}\hat{\beta}$ 이다. $(\mathbf{x} = (\mathbf{x}_1, …, \mathbf{x}_N)^T, \ \mathbf{y} = (\mathbf{y}_1, …, \mathbf{y}_N)^T)$. 다음으로 inputs $\mathbf{x}_1, …, \mathbf{x}_p$가 직교한다면(모든 $j \neq k$에 대해 $\left\langle \mathbf{x}_j, \mathbf{x}_k \right\rangle = 0$) 모든 $\hat{\beta}_j$는 $\frac{\left\langle \mathbf{x}_j, \mathbf{y} \right\rangle}{\left\langle \mathbf{x}_j, \mathbf{x}_j \right\rangle}$로 표현할 수 있다. 보통 designed matrix의 column vector들은 직교하지 않으므로 그람-슈미트 직교화를 이용하여 연속적으로 회귀계수를 다음과 같이 찾을 수 있다.

즉 모든 $j$마다 이전 직교기저들과 수직인 벡터 $\mathbf{z}_j$을 찾아 $\mathbf{y}$를 $\mathbf{z}_p$에 정사영시킨 벡터를 찾는 과정이다. 최종적으로 얻은 회귀계수는 $\hat{\beta}_p =\frac{\left\langle \mathbf{z}_p, \mathbf{y} \right\rangle}{\left\langle \mathbf{z}_p, \mathbf{z}_p \right\rangle}$이다. 2번 단계에서 $\mathbf{x}_j$는 $ \mathbf{z}_1,.., \mathbf{z}_j $들의 선형결합이므로 $\mathbf{z}_1,.., \mathbf{z}_p$는 designed matrix $\mathbf{X}$의 열공간의 기저임을 알 수 있다. 또한 모든 $j$에 대해 $\mathbf{x}_j$는 $\mathbf{z}_j$에만 포함되므로, $\hat{\beta}_p$는 $\mathbf{y}$에 대한 $\mathbf{x}_p$의 회귀계수로 볼 수 있다. 또한 $Var(\hat{\beta}_p) = \frac{\sigma^2}{|| \mathbf{z}_p || ^2}$로 $\mathbf{z}_p$의 길이에 따라 달라지는데, 이는 다른 $\mathbf{x}_k$들에서 설명할 수 없는 $\mathbf{x}_p$의 정도를 나타낸다. 만약 $\mathbf{x}_p$가 어떤 $\mathbf{x}_k$와 높은 상관관계를 갖는다면, 잔차 벡터인 $\mathbf{z}_p$는 0에 가까워지고 따라서 $\mathbf{x}_p$가 매우 불안정한 값을 가질 수 있다.

이를 QR 분해를 이용하여 행렬 형태로 아래와 같이 나타낼 수 있다.

\[\mathbf{X} = \mathbf{Z} \mathbf{\Gamma} \ (\mathbf{Z} = (\mathbf{z}_1, ..., \mathbf{z}_p), \ \mathbf{\Gamma} \text{는} \ \hat{\gamma}_{lj} \text{를 원소로 가지는 상삼각 행렬} )\]

$j$번째 대각 성분이 $| | \mathbf{z}_j | |$인 대각 행렬 $\mathbf{D}$를 정의하면 아래와 같이 QR분해를 할 수 있다.

\[\begin{align*} \mathbf{X} &= \mathbf{Z}\mathbf{\Gamma} \\ &= \mathbf{Z}\mathbf{D}^{-1}\mathbf{D}\mathbf{\Gamma} \\ &= \mathbf{Q}\mathbf{R} \ ( \mathbf{Q}^T\mathbf{Q} = \mathbf{I}, \ \mathbf{R} \text{은 상삼각행렬}) \end{align*}\]

이를 통해 최소제곱해를 다음과 같이 나타낼 수 있다.

\[\begin{align*} \hat{\beta} &= (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T \mathbf{y} \\ &= (\mathbf{R}^T\mathbf{R})^{-1}\mathbf{R}^T\mathbf{Q}^T\mathbf{y} \\ &= \mathbf{R}^{-1}\mathbf{Q}^T\mathbf{y} \\ \\ \hat{\mathbf{y}} &= \mathbf{X}\hat{\beta} \\ &= \mathbf{Q}\mathbf{R}\mathbf{R}^{-1}\mathbf{Q}^T\mathbf{y} \\ &= \mathbf{Q}\mathbf{Q}^T\mathbf{y} \end{align*}\]

상삼각행렬의 역행렬은 back substitution을 통해 쉽게 계산할 수 있으므로 $\mathbf{X}^T\mathbf{X}$의 역행렬을 구할때보다 계산상의 이점이 있다.

 

Subset selection

우리가 OLS에서 회귀계수를 모두 선택하지 않는데는 2가지 이유가 있다. 첫번째로 prediction accuracy 때문이다. OLS는 종종 낮은 편향과 높은 분산을 갖는다. prediction accuracy는 몇몇 계수들을 0으로 만들거나 줄이면서 향상될 수 있는데, 이를 통해 어느정도의 편향을 희생하면서 predicted value들의 분산을 줄일 수 있어 전반적인 prediction accuracy를 향상시킬 수 있다. 두번째로 해석력의 관점에서 우리는 강한 영향을 주는 비교적 적은 subset을 결정하고 싶어한다. 큰그림을 얻기 위해서는 몇몇의 작은 디테일들은 희생할 줄 알아야 한다.

Forward-Stepwise Selection

Forward-Stepwise Selection은 절편을 시작으로 매 iteration마다 가장 높은 예측값을 내는 변수를 선택하는 방법이다. 그리디한 알고리즘이기에 최적의 모델을 고르지 못할 수도 있지만, $p \gg N$인 경우에서도 계산이 가능하고, 이러한 제한적인 탐색방법 덕분에 best-subset selection에 비해 높은 편향을 가질 수도 있지만 낮은 분산을 얻을 수 있다는 이점이 있다. 예를들어 $ \mathbf{X}_1 = (X_1, … X_q)$가 얻어졌고, 새로운 $X_k(q < k \leq p)$를 RSS를 최소로 하도록 뽑으려 한다면 다음과 같이 진행될 수 있다.

1. $ \mathbf{X}_1 = \mathbf{Q}_1 \mathbf{R}_1$ 로 QR 분해한다.

2. 그람-슈미트 직교화를 이용하여 $\mathbf{Q}_1 = (\mathbf{q}_1, …, \mathbf{q}_q) $의 컬럼벡터들과 직교하는 \(\mathbf{r}_k = X_k - \sum_{j=1}^{q} (X_k^T \mathbf{q}_j)\mathbf{q}_j\) 를 잡는다. $\mathbf{r}_k$의 단위벡터를 $\mathbf{q}_k$라 하면, $X_k$를 현재 $\mathbf{X}_1$에 추가한 새로운 예측값은

   \[\begin{align*} \mathbf{\hat{y}}^+ &= \mathbf{\hat{y}} + (\mathbf{q}_k^T \mathbf{y})\mathbf{q}_k \\ &= \mathbf{\hat{y}} + (\mathbf{q}_k^T (\mathbf{\hat{y}} + \mathbf{r}_k))\mathbf{q}_k \\ &= \mathbf{\hat{y}} + (\mathbf{q}_k^T \mathbf{r}_k)\mathbf{q}_k \ (\hat{\mathbf{y}}\text{는} \ \mathbf{q}_1, ..., \mathbf{q}_q \text{의 선형결합이므로 )} \end{align*}\]

   이다.($\mathbf{r}_k$는 업데이트 전 현재 잔차) 따라서 RSS는 $ (\mathbf{q}_k^T \mathbf{r}_k)^2$에 의해 줄어든다.

3. 따라서 매 iteration마다, \(k^* = \underset{q < k \leq p}{\mathrm{argmax}} \ \| \mathbf{q}_k^T \mathbf{r}_k \|\)를 찾아 \(q_{q+1} = \mathbf{q}_{k^*}\)로 업데이트해준다. (Note. 변수를 추가할수록 RSS는 줄어든다.)

Backward-Stepwise Selection

Backward-Stepwise Selection은 반대로, 풀모델에서 시작해서 예측값에 가장 낮은 영향력을 보이는 변수를 제거하는 방법이다. Forward-Stepwise Selection와 마찬가지로 RSS를 이용해서 매 단계마다 변수를 제거해야 한다면 다음과 같이 진행될 수 있다. 먼저 k번째 단계에서 모델의 RSS를 $RSS_1$이라하고, $RSS_j$를 현재 모델이 갖고 있는 변수중 $j$번째 변수를 제거한 모델의 RSS라 한다면 F-statistic과 유사하다. $F_j = \frac{RSS_j - RSS_1}{RSS_1 / (N-p_1-1)}$이고 분모는 $j$와 관계가 없기 때문이다. 따라서 하나의 변수를 제거하는 $F_j$는 $z_j^2$와 같으므로, 매단계마다 z-score가 가장 작은 변수를 제거하면 된다. 유의할 점은 Backward-Stepwise Selection은 $N>p$인 경우에만 사용이 가능하다.

 

Note. 하나의 변수를 제거하는 F-statistic이 z-score의 제곱과 같은 이유

하나의 변수를 제거한 모델과의 F-statistic은 $F = \frac{RSS_0 - RSS_1}{N-p_1-1}$이고 $\hat{\sigma}^2 = \frac{RSS_1}{N-p_1-1}$이므로, $F = \frac{RSS_0 - RSS_1}{\hat{\sigma}^2}$로 나타낼 수 있다. \(z_j = \frac{\hat{\beta}_j}{\hat{\sigma}\sqrt{v_{jj}}}\) ($v_{jj}$는 $(\mathbf{X}^T\mathbf{X})^{-1}$의 j번째 대각성분) 이므로 \(RSS_1 - RSS_0 = \frac{\hat{\beta}_j^2}{v_{jj}}\) 임을 확인하면 된다. $RSS_1$은 이미 우리가 알고 있기에 $RSS_0$을 구하면 충분하다. $RSS_0$은 다음과 같이 $\beta$의 $j$번째 원소를 0이라고 넣고 이를 최소화하는 RSS를 구하는 것과 같다.

\[min_{\beta} \| \mathbf{y} - \mathbf{X}\beta \|^2 \ \text{ subject to j-th elment of } \ \beta \text{ is 0.}\]

$e_j$를 $j$번째 원소만 1이고 나머지는 0인 컬럼벡터로 정의하면, 제약조건을 $e_j^T \beta = 0$로 나타낼 수 있다. 이를 라그랑주 승수법을 이용하여 쌍대문제로 변환하면 $\mathcal{L}(\beta, \lambda) = (\mathbf{y} - \mathbf{X}\beta)^T(\mathbf{y} - \mathbf{X}\beta) + \lambda e_j^T\beta \ $이다. 따라서 미분을 통해 reduced 모델의 $\hat{\beta}^{(new)}$을 구하면 아래와 같다.

\[\begin{align*} \frac{\partial \mathcal{L}(\beta, \lambda)}{\partial \beta} &= -2\mathbf{X}^T(\mathbf{y} - \mathbf{X}\beta) + \lambda e_j = 0 \\ \hat{\beta}^{(new)} &= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} - \frac{\hat{\lambda}^{(new)}}{2}(\mathbf{X}^T\mathbf{X})^{-1}e_j \\ &= \hat{\beta} - \frac{\hat{\lambda}^{(new)}}{2}(\mathbf{X}^T\mathbf{X})^{-1}e_j \end{align*}\]

$e_j^T \beta = 0$이므로, $e_j^T\hat{\beta} = \frac{\hat{\lambda}^{(new)}}{2}e_j^T(\mathbf{X}^T\mathbf{X})^{-1}e_j \ $, $\hat{\lambda}^{(new)} = \frac{2 e_j^T\hat{\beta}}{e_j^T(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^Te_j}$이다. 따라서 $RSS_0$는 다음과 같이 나타낼 수 있다.

\[\begin{align*} RSS_0 &= (\mathbf{y} - \mathbf{X}\hat{\beta}^{(new)})^T(\mathbf{y} - \mathbf{X}\hat{\beta}^{(new)}) \\ &= (\mathbf{y} - \mathbf{X}\hat{\beta})^T(\mathbf{y} - \mathbf{X}\hat{\beta}) + 2(\mathbf{y} - \mathbf{X}\hat{\beta})^T\mathbf{X}\frac{\hat{\lambda}^{(new)}}{2}(\mathbf{X}^T\mathbf{X})^{-1}e_j + \frac{\hat{\lambda}^{(new)^2}}{4}e_j^T(\mathbf{X}^T\mathbf{X})^{-1}e_j \\ &= RSS_1 + (\frac{2 e_j^T\hat{\beta}}{e_j^T(\mathbf{X}^T\mathbf{X})^{-1}e_j})^2\frac{e_j^T(\mathbf{X}^T\mathbf{X})^{-1}e_j}{4} \\ &= RSS_1 + \frac{(e_j^T\hat{\beta})^2}{e_j^T(\mathbf{X}^T\mathbf{X})^{-1}e_j} \\ &= RSS_1 + \frac{\hat{\beta}_j^2}{v_{jj}} \end{align*}\]

 

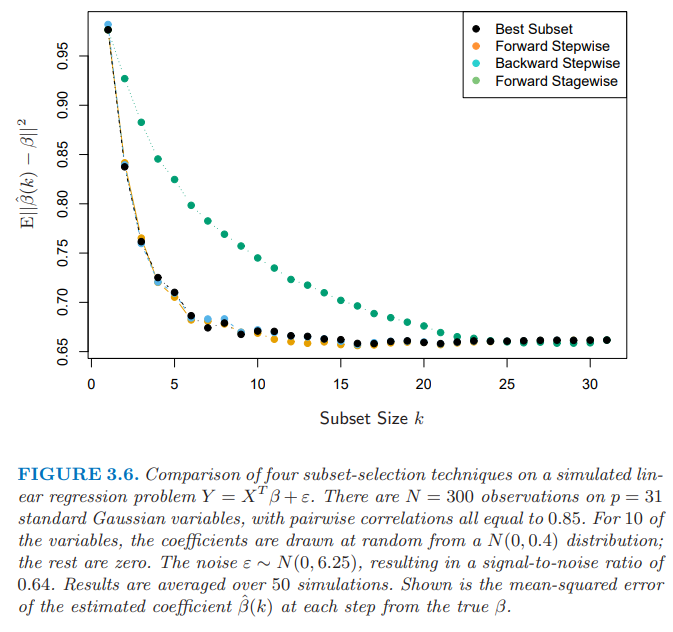
다음 그래프는 subset selection방법들을 비교한 결과이다. Foward-Stagewise Selection은 다음 포스팅에서 다뤄볼 예정이다.