[ESL 리뷰] 교재 4-1장 LDA

“The Elements of Statistical Learning” 교재 4장 Linear Methods for Classification 내용을 요약한 것이다. Classification 문제에서는 종속 변수가 이산적인 값을 갖기에 input space에 대한 분리가 항상 가능하다. 이 때의 분류 경계를 decision boundary라고 하며, 이번 절에서는 decision boundary가 linear한 모델에 대해서만 다룰 것이다. 들어가기에 앞서 Statistical Decision Thoery에 대해 다시 복습해보자.

Statistical Decision Theory

독립변수인 \(p\)차원 벡터 \(X\)와 종속변수인 실수 \(Y\)에 대해 joint distribution인 \(Pr(X,Y)\)를 가정하자. 지도학습의 목적은 적절한 loss function에 대해 이를 최적화하는 estimator \(f(X)\)를 찾는 것이다. 즉 다음의 expected prediction error(EPE)를 최소화하는 \(f\)를 찾는 것이다.

\[\text{EPE}(f) = \mathbb{E}_{X,Y}\left[L(Y, f(X)) \right]\]

Classification 문제의 경우 종속변수가 discrete하므로 \(K\)개의 클래스를 갖는다고 가정하면, EPE는 다시 다음과 같이 나타낼 수 있다.

\[\begin{align*} \text{EPE} &= \mathbb{E}\left[ L(G, \hat{G}(X))\right] \text{ where } \hat{G} \in \mathcal{G}=(\mathcal{G}_1,...,\mathcal{G}_K) \\ &= \mathbb{E}_X \sum_{k=1}^K L(\mathcal{G}_k, \hat{G}(x))Pr(G=\mathcal{G}_k|X) \end{align*}\]

따라서 이는 임의의 지점 \(X=x\)마다의 최솟값을 내는 함수가 가장 최적의 \(f\)이다. 즉,

\[\hat{G}(x) = \underset{g \in \mathcal{G}}{\text{arg min}} \sum_{k=1}^K L(\mathcal{G}_k, g)Pr(G=\mathcal{G}_k|X=x)\]

이다.

이제 특정 loss function을 정의하여 특정한 \(\hat{G}(x)\)를 구해보자. Classification에서 가장 많이 사용되는 loss function은 0-1 loss라고 불리는 \(L(Y,f(X)) = I(Y \neq f(X))\)이다. 이를 대입하여 \(\hat{G}(x)\)를 구하면 다음과 같다.

\[\begin{align*} \hat{G}(x) &= \underset{g \in \mathcal{G}}{\text{arg min}} \sum_{g \neq \mathcal{G}}Pr(G=\mathcal{G}_k|X=x) \\ &= \underset{g \in \mathcal{G}}{\text{arg min}} \ \left[ 1 - Pr(G=g|X=x) \right] = \underset{g \in \mathcal{G}}{\text{arg max}} \ Pr(G=g|X=x) \end{align*}\]

즉 input variable \(x\)에 대한 posterior에서 확률이 가장 큰 클래스를 찾는 것이다. 이를 Bayes classifier라고 부르기도 한다.

Linear Regression of an Indicator Matrix

해당 모델은 먼저, 반응변수를 indicator variable(dummy variable)로 처리를 해준다. 즉 \(\mathcal{G}\)가 \(K\)개의 클래스를 갖는다면 종속변수 \(Y = (Y_1, ..., Y_K)\)로 나타내고, 각 \(Y_k\)는 \(G=k\)일 경우에 1, 나머지는 0으로 처리한다. \(N\)개의 학습 데이터에 대해서는 \(N \times K\) 행렬인 \(\mathbf{Y}\)로 나타낼 수 있을 것이다. 변수 처리를 하였으면 이후에는 Linear regression 모델을 fit한다. 즉 다음과 같이 나타낼 수 있다.

\[\hat{\mathbf{Y}} = \mathbf{X} (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y} = \mathbf{X}\hat{\mathbf{B}}\]

새로운 관측 데이터 \(x\)가 들어오면 다음과 같이 $K$ vector인 \(\hat{f}(x)\)를 구하여 최대가 되는 인덱스가 예측한 클래스일 것이다.

\[\hat{f}(x)^T = (1, x^T) \hat{\mathbf{B}} = (\hat{f}_1(x), ... ,\hat{f}_K(x)) \in \mathbb{R}^{1 \times K}\] \[\hat{G}(x) = \underset{k\in\mathcal{G}}{\mathrm{argmax}} \hat{f}_k(x)\]

이번에는 해당 모델이 어떻게 가능한 것일까 생각해보자. Linear regression의 경우 조건부 기댓값을 추정하는 것임을 우리는 알 고 있다. indicator variable에 대해서는 확률변수인 \(Y_k\)가 \(k=K\)일 때는 1, 나머지는 0을 갖으므로 이에 대한 조건부 기댓값은 다음과 같다.

\[\mathbb{E}(Y_k | X=x) = Pr(G=k|X=x)\]

위의 Statistical Decision Thoery에서 보았듯이, \(hat{G}(x)\)는 사후확률 가장 높은 클래스를 찾는 것임을 유의하면, Linear regression에서의 \(\hat{f}_k(x)\)는 조건부 기댓값이 아닌, 우변의 사후확률을 추정하는 과정이라고 보는 것이 합리적이다. 그렇다면 \(\hat{f}_k(x)\)가 과연 확률을 잘 추정할 수 있을까?

가장 직관적인 방법은 모든 확률을 더하면 1이므로, \(\sum_{k=1}^Kf_k(x) = 1\)임을 확인해보자. 먼저 designed matrix를 다음과 같이 쪼개볼 수 있다.

\[\mathbf{X} = \begin{pmatrix} \mathbf{1}_N \ \mathbf{x} \end{pmatrix} \ \text{where} \ \mathbf{x} = (x_1,...,x_N)^T\] \[\mathbf{X}^T \mathbf{X} = \begin{pmatrix} \mathbf{1}_N^T \\ \mathbf{x}^T \end{pmatrix}\begin{pmatrix} \mathbf{1}_N & \mathbf{x} \end{pmatrix} = \begin{pmatrix} N & \mathbf{1}_N^T\mathbf{x} \\ \mathbf{x}^T\mathbf{1}_N & \mathbf{x}^T\mathbf{x} \end{pmatrix}\]

이제 임의의 input variable \(x\)에 대하여 \(f_k(x)\)의 합을 구해보자. (Note. 마지막 계산과정은 역행렬의 성질을 이용한 것이다.)

\[\begin{align*} \sum_{k \in \mathcal{G}} \hat{f}_k(x) &= (1, x^T) \hat{\mathbf{B}}\mathbf{1}_K \\ &= (1, x^T)(\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\mathbf{1}_K \\ &= (1, x^T)\begin{pmatrix} N & \mathbf{1}_N^T\mathbf{x} \\ \mathbf{x}^T\mathbf{1}_N & \mathbf{x}^T\mathbf{x} \end{pmatrix}^{-1}\begin{pmatrix} \mathbf{1}_N^T \\ \mathbf{x}^T \end{pmatrix}\mathbf{1}_N \\ &= (1, x^T)\begin{pmatrix} N & \mathbf{1}_N^T\mathbf{x} \\ \mathbf{x}^T\mathbf{1}_N & \mathbf{x}^T\mathbf{x} \end{pmatrix}^{-1} \begin{pmatrix} N \\ \mathbf{x}^T\mathbf{1}_N \end{pmatrix} = (1,x^T)\begin{pmatrix} 1 \\ \mathbf{0}_p \end{pmatrix} = 1 \end{align*}\]

즉, \(\sum_{k=1}^Kf_k(x) = 1\)이다. 하지만, \(f_k(x)\)는 반드시 0과 1사이에 값이라는 것을 보장할 수 없다. 이에 대해서는 softmax 함수 \(\sigma(z) = e^{z_i} / \sum_{j=1}^K e^{z_j}\)를 이용하면 해결될 것이다. 하지만 Linear regression에서는 masking effect라는 큰 문제가 발생한다. 이는 다음 그림처럼 가운데 클래스가 가려져서 제대로 분류가 이뤄지지 않는 현상으로 자세한 내용은 밑에서 다뤄볼 것이다.

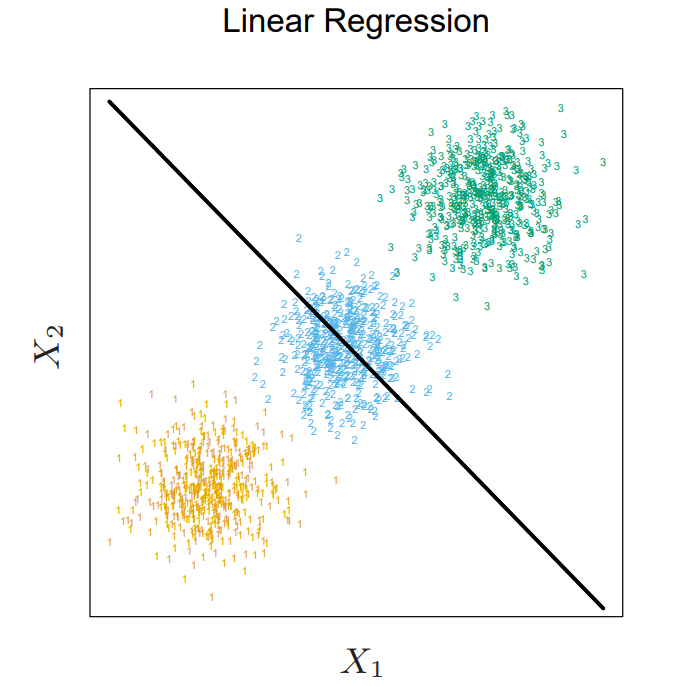
\(f_k(x)\)값을 비교해보면, 가운데 2 클래스에 대한 예측값이 모든 구간에서 가장 높은 경우가 없으므로 선택되지 않는다.

 

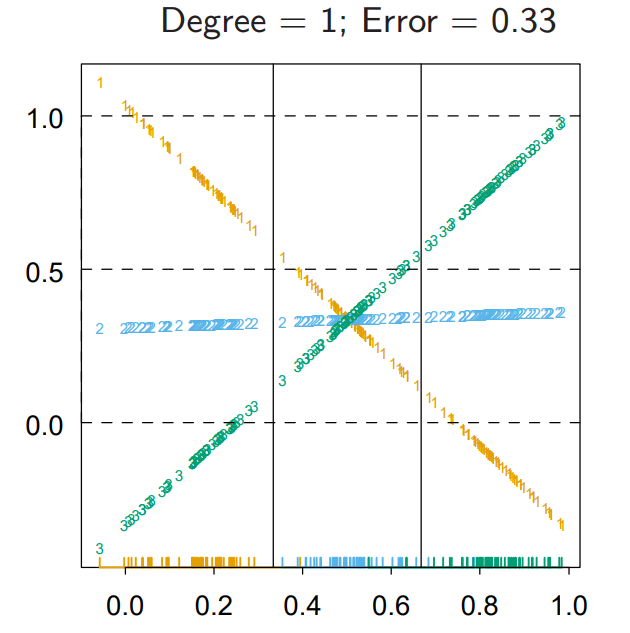
Linear Discriminant Analysis

분류문제에서는 사후 확률을 잘 예측하는 모델을 찾는 것이 중요함을 위에서 볼 수 있었다. 따라서 LDA는 다음과 같은 사후 분포를 가정하여 예측을 진행한다.

먼저 prior인 \(\pi_k\)가 \(\sum_{k=1}^K \pi_k=1\)이 되도록 정의하고, 조건부 분포인 \(f_k(x)\)도 정의하자. 종속변수가 이산이기에 \(Pr(X=x)\)는 다음과 같이 나타낼 수 있다.

\[Pr(X=x) =\sum_{k\in \mathcal{G}}Pr(X=x|G=k)Pr(G=k)\]

즉, 베이즈 정리를 이용하면 posterior를 다음과 같이 쓸 수 있다.

\[Pr(G=k|X=x) = \frac{Pr(X=x|G=k)Pr(G=k)}{Pr(X=x)} = \frac{f_k(x)\pi_k}{\sum_{l=1}^K f_l(x)\pi_l}\]

여기서 \(f_k\)가 다음과 같은 다변량 정규 분포를 따진다고 가정하자.

\[f_k(x) = \mathcal{N}(\mu_k, \Sigma_k) = \frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}}\exp(-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k))\]

마지막으로, LDA는 위의 covariance \(\Sigma_k\)가 \(\Sigma\)로 모두 같다는 가정을 추가한다. 이제, LDA의 decision boundary가 linear한지 확인해보자. 이는 log ratio가 linear임을 확인하면 충분한데, 이유는 다음과 같다.

\[\{ x: Pr(G=k|X=x) = Pr(G=l | X=x) \} = \{ x: \log{\frac{Pr(G=k|X=x)}{Pr(G=l | X=x)}=0} \}\]

LDA의 log ratio는 다음과 같다.

\[\log{\frac{Pr(G=k|X=x)}{Pr(G=l | X=x)}} = \log \frac{\pi_k}{\pi_l} - \frac{1}{2}(\mu_k + \mu_l)^T\Sigma^{-1}(\mu_k - \mu_l) + x^T\Sigma^{-1}(\mu_k - \mu_l)\]

즉, \(x\)에 대하여 linear하다는 것을 확인할 수 있다. 마찬가지로 LDA의 예측값은 다음 discriminant function \(\delta_k(x)\)가 가장 큰 \(k\)이다.

\[\delta_k(x) = x^T\Sigma^{-1}\mu_k - \frac{1}{2}\mu_k^T\Sigma^{-1}\mu_k + \log \pi_k\]

하지만 실제 데이터에서는 위의 정규 분포 내의 파라미터를 알 수 없으므로, 가지고 있는 데이터를 활용하여 다음과 같은 예측값을 사용한다. ( \(\hat{\Sigma}\)는 클래스마다 나눠 분산을 구해 이를 합친 pooled covariance을 사용함에 유의하자.)

\[\begin{align*} \hat{\pi}_k &= \frac{N_k}{N} \ \text{where} \ N_k \ \text{is the number of class-k observations} \\ \hat{\mu}_k &= \frac{1}{N_k}\sum_{g_i = k}x_i \\ \hat{\Sigma}&= \sum_{k=1}^K\sum_{g_i = k}\frac{1}{N-K}(x_i - \hat{\mu}_k)(x_i - \hat{\mu}_k)^T \ \text{(pooled covariance, within-class covariance)} \end{align*}\]

 

Covariance Decomposition

데이터의 전체 분산 total covariance는 위의 LDA에서 처럼 클래스 내의 분산의 합동 분산인 within-class covariance와 클래스 간 분산인 between-class covariance로 쪼갤 수 있다. 먼저 total covariance를 구하기 위해 다음과 같이 \(\hat{\mu}\)를 정의해보자.

\[\bar{\mu} = \frac{1}{N}\sum_{i=1}^N x_i = \frac{1}{N}\sum_{k=1}^KN_k\hat{\mu}_k\]

이제 total covariance, within-class covariance, between-class covariance를 각각 구하면 다음과 같고, within-class covariance 와 between-class covariance의 합이 total covariance임을 쉽게 확인해 볼 수 있다.

\[\begin{align*} \hat{\Sigma}_T &= \frac{1}{N}\sum_{i=1}^N (x_i-\bar{\mu})(x_i-\bar{\mu})^T = \frac{1}{N} \left[ \sum_{i=1}^N x_ix_i^T - N\bar{\mu}\bar{\mu}^T \right] \ \text{(total covariance)} \\ \hat{\Sigma}_W &= \frac{1}{N}\sum_{k=1}^K\sum_{g_i = k}(x_i - \hat{\mu}_k)(x_i - \hat{\mu}_k)^T = \frac{1}{N}\sum_{k=1}^K\left[ \sum_{g_i = k} x_ix_i^T - N_k\hat{\mu}_k\hat{\mu}_k^T \right] = \frac{1}{N}\left[ \sum_{i=1}^N x_ix_i^T - \sum_{k=1}^KN_k\hat{\mu}_k\hat{\mu}_k^T \right] \ \text{(within-class covariance)} \\ \hat{\Sigma}_B &= \frac{1}{N}\sum_{k=1}^KN_k(\hat{\mu}_k - \bar{\mu})(\hat{\mu}_k - \bar{\mu})^T = \frac{1}{N}\left[ \sum_{k=1}^KN_k\hat{\mu}_k\hat{\mu}_k^T - N\bar{\mu}\bar{\mu}^T \right] \ \text{(between-class covariance)} \end{align*}\]

LDA and Linear Regression in Binary Classification

이번에는 클래스가 2개인 이진분류 문제에서 LDA와 Linear Regression이 상당히 유사하게 작동한다는 것을 확인해 볼 것이다. \(N\)개의 데이터셋에 대하여 각 클래스에 속하는 샘플 개수를 \(N_1, N_2\)라고 하고 각각의 \(Y\)를 \(\frac{N}{N_1}, \frac{N}{N_2}\)로 나타내보자. 먼저 LDA의 경우 다음과 같은 경우에 클래스 2를 예측할 것이다.

\[x^T\Sigma^{-1}(\hat{\mu}_2 - \hat{\mu}_1) > \frac{1}{2}\hat{\mu}_2^T\Sigma^{-1}\hat{\mu}_2 - \frac{1}{2}\hat{\mu}_1^T\Sigma^{-1}\hat{\mu}_1 + \log \frac{N_1}{N} - \log \frac{N_2}{N}\]

이제 Linear Regression의 경우를 살펴보자. \(\hat{\beta}\)를 행렬 표현으로 나타내면 다음과 같다.

\[\begin{align*} \mathbf{X}^T\mathbf{X}\begin{pmatrix} \hat{\beta}_0 \\ \hat{\beta} \end{pmatrix} &= \mathbf{X}^T\mathbf{Y} \\ \begin{pmatrix} N & \mathbf{1}_N^T\mathbf{x} \\ \mathbf{x}^T\mathbf{1}_N & \mathbf{x}^T\mathbf{x} \end{pmatrix}\begin{pmatrix} \hat{\beta}_0 \\ \hat{\beta} \end{pmatrix} &=\begin{pmatrix} \mathbf{1}_N^T\mathbf{Y} \\ \mathbf{x}^T\mathbf{Y}\end{pmatrix}\\ \end{align*}\]

즉, 위를 다시 \(\hat{\beta}_0, \hat{\beta}\)에 대하여 나타내면 다음과 같다.

\[\begin{align*} \hat{\beta}_0 &= \frac{1}{N}\sum_{i=1}^NY_i - \frac{1}{N}\sum_{i=1}^Nx_i^T\hat{\beta} = - \frac{1}{N}\sum_{i=1}^Nx_i^T\hat{\beta} \\ (\sum_{i=1}^N x_ix_i^T - \frac{1}{N}\sum_{i=1}^N x_i\sum_{i=1}^N x_i^T)\hat{\beta} &= \sum_{i=1}^NY_ix_i - \frac{1}{N} \sum_{i=1}^N Y_i\sum_{i=1}^N x_i = \sum_{i=1}^NY_ix_i \end{align*}\]

먼저 $\hat{\beta}$를 구하기 위해서는 \(\sum_i x_i, \sum_i Y_i, \sum_i x_iY_i\)를 계산해야 한다. 이를 LDA의 파라미터를 이용해서 나타내면 다음과 같다.

\[\sum_{i=1}^N x_i =\sum_{i:g_i=1}x_i + \sum_{i:g_i=2}x_i = N_1\hat{\mu}_1 + N_2\hat{\mu}_2, \ \sum_{i=1}^N Y_i = 0, \ \sum_{i=1}^Nx_iY_i = -\frac{N}{N_1}N_1\hat{\mu}_1 + \frac{N}{N_2}N_2\hat{\mu}_2 = N(\hat{\mu}_2 - \hat{\mu_1})\]

또한 \(\hat{\Sigma}\)를 $x_i,Y_i$에 대하여 나타내면 다음과 같다.

\[\begin{align*} \hat{\Sigma} &= \frac{1}{N-2}(\sum_{i:g_i=1}(x_i-\hat{\mu}_1)(x_i-\hat{\mu}_1)^T + \sum_{i:g_i=2}(x_i-\hat{\mu}_2)(x_i-\hat{\mu}_2)^T) \\ &= \frac{1}{N-2}(\sum_{i=1}^Nx_ix_i^T -N_1\hat{\mu}_1\hat{\mu}_1^T - N_2\hat{\mu}_2\hat{\mu}_2^T) \end{align*}\]

따라서 이들를 대입하여 \(\hat{\beta}\)를 구하면 다음과 같다.

\[\begin{align*} (\sum_{i=1}^N x_ix_i^T - \frac{1}{N}\sum_{i=1}^N x_i\sum_{i=1}^N x_i^T)\hat{\beta} &= ((N-2)\hat{\Sigma} + N_1\hat{\mu}_1\hat{\mu}_1^T + N_2\hat{\mu}_2\hat{\mu}_2^T - \frac{1}{N}(N_1\hat{\mu}_1+N_2\hat{\mu}_2)(N_1\hat{\mu}_1^T+N_2\hat{\mu}_2^T))\hat{\beta} \\ &= ((N-2)\hat{\Sigma} +\frac{N_1N_2}{N}(\hat{\mu}_2-\hat{\mu}_1)(\hat{\mu}_2-\hat{\mu}_1)^T)\hat{\beta} = N(\hat{\mu}_2 - \hat{\mu}_1) \end{align*}\]

\((\hat{\mu}_2-\hat{\mu}_1)^T\hat{\beta}\)가 스칼라 값이라는 점을 유의하면 \(\hat{\beta}\)는 \(\hat{\Sigma}^{-1}(\hat{\mu}_2 - \hat{\mu}_1)\)과 비례관계이며, 이는 LDA의 $x$의 계수임을 알 수 있다. 따라서 LDA의 진행방향과 비례함을 알 수 있다.

이번에는 \(\hat{\beta}_0\)을 구해보면 완전히 LDA와 같지는 않음을 알 수 있다. 또한 이는 이진분류에서만 해당됨에 유의하자.

Masking effect

이번에는 Linear Regression에서의 masking effect에 대해서 이것이 왜 발생하고, LDA에서는 발생하지 않음을 확인해 볼 것이다. 이는 위 서 살펴본 covariance decomposition와 관련이 있다.

먼저 Linear Regression의 \(\hat{G}(x)\)를 구하는 과정을 다시 살펴보자.

\[\begin{align*} \hat{G}(x) &= \underset{k\in\mathcal{G}}{\mathrm{argmax}} \left( x^T (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\right)_k + \frac{N_k}{N} \\ &= \underset{k\in\mathcal{G}}{\mathrm{argmax}} \ x^T\hat{\Sigma}_T^{-1}\frac{1}{N}\sum_{g_i = k}x_i + \frac{N_k}{N} \\ &= \underset{k\in\mathcal{G}}{\mathrm{argmax}} \frac{N_k}{N}x^T\hat{\Sigma}_T^{-1}\hat{\mu}_k + \frac{N_k}{N} \end{align*}\]

이는 다음 \(\delta_k(x)\)를 최소화 하는 것과 같다. (아래 식을 풀어서 \(-1\)을 곱하면 위와 같다.)

\[\delta_k(x) = \frac{N_k}{2N}\{ (x-\hat{\mu}_k)^T\hat{\Sigma}_T^{-1}(x-\hat{\mu}_k)- x^T\hat{\Sigma}_T^{-1}x - \hat{\mu}_k^T\Sigma_T^{-1}\hat{\mu}_k-2 \}\]

수식의 간결성을 위해서 prior \(\pi_l\)는 모두 같은 확률을 같고 있다고 가정하자. 이 때의 LDA의 discriminant function은 다음과 같다. 즉, \(\hat{\Sigma}_{W}\)를 사용한 마할라노비스 거리이다.

\[\delta_k(x) = (x-\hat{\mu}_k)^T\hat{\Sigma}_W^{-1}(x-\hat{\mu}_k)\]

반면, Linear Regression은 \(\hat{\Sigma}_{T}\)를 사용한 마할라노비스 거리와 \(\hat{\mu}_k\)가 포함된 추가적인 항이 더해진다.

\[\delta_k(x) = (x-\hat{\mu}_k)^T\hat{\Sigma}_T^{-1}(x-\hat{\mu}_k)- \hat{\mu}_k^T\Sigma_T^{-1}\hat{\mu}_k\]

따라서 두 모델 모두 마할라노비스 거리라는 같은 거리 측도를 사용하지만 LDA의 경우 클래스간 pooled covariance를, Linear Regression은 total covariance를 사용하는데 차이가 있고 추가적인 항이 더해진다. Linear Regession에서 masking effect가 발생하는 이유가 여기에 있다. 클래스간 분류를 하는데 있어서 metric으로 between covariance가 더해진 covariance를 사용하기에 왜곡 현상이 발생하고, 추가적인 항에서 centriod의 배치에 의한 영향을 또 한 번 받는다. 다음 그림을 살펴보자.

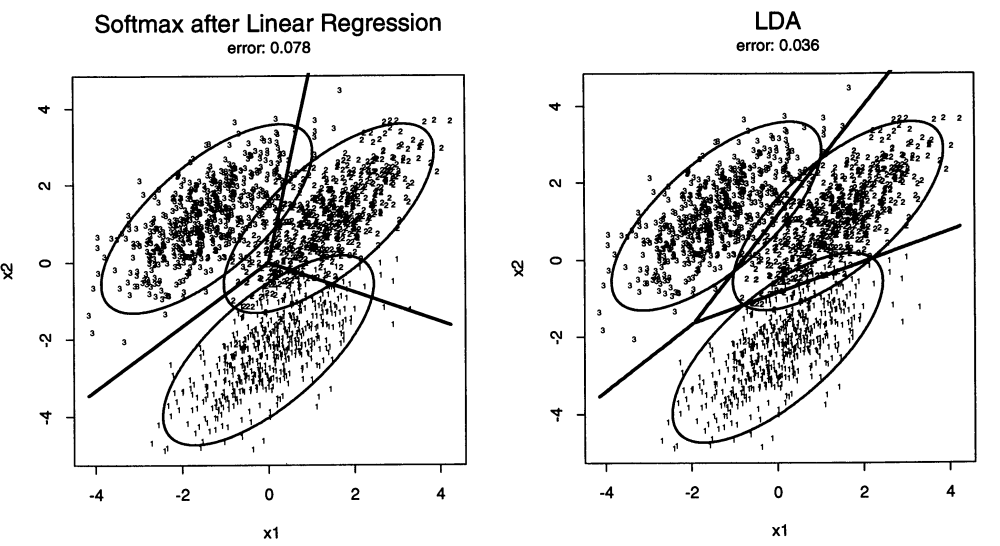
첫번째 그림은 softmax 함수를 이용한 Linear Regression이고 두번째 그림은 LDA의 결과이다. centriod간의 분산이 더해진 total covariance를 사용한 Linear Regression에서 분류에 필요 없는 centriod의 위치를 고려한 왜곡에 대한 bias가 decison boundary에 발생함을 알 수 있다. 하지만 LDA에서는 그러한 왜곡이 발생하지 않았음을 볼 수 있다. 다음 그림은 Linear regression의 추가적인 항으로 인해 발생한 현상이다.

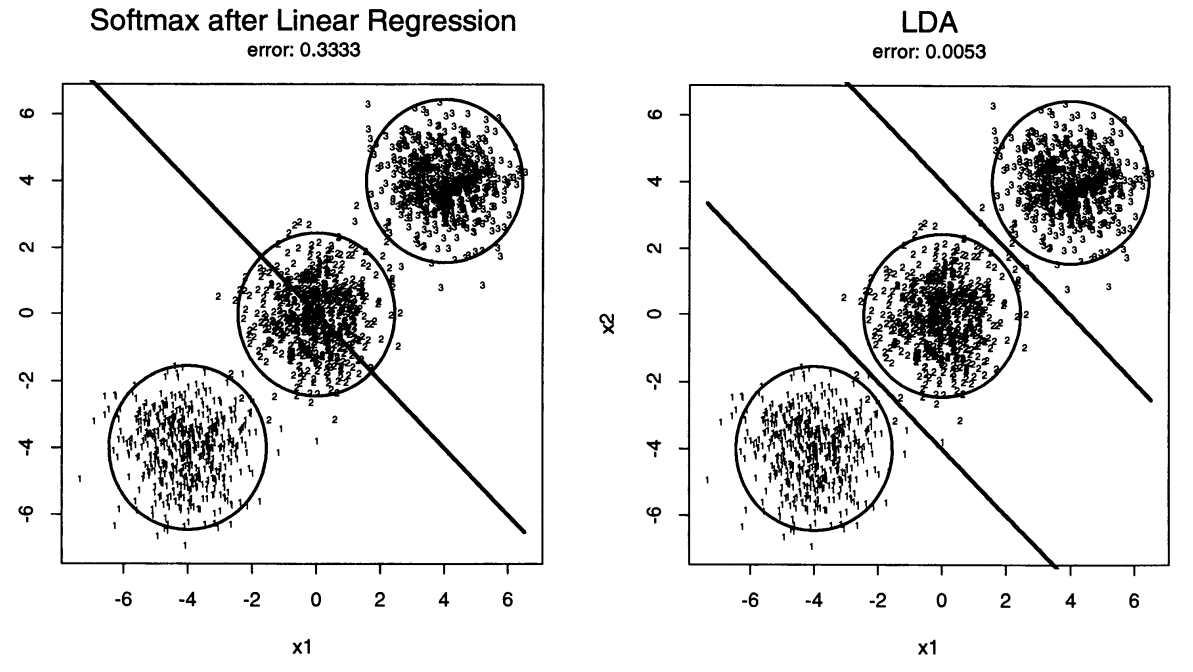
centriod가 colinear하게 배치되어 클래스 2의 centriod \(\hat{\mu}_2 = 0\)이고, 클래스 2기준으로 양쪽 클래스 1,3에 거의 동일한 \(-\hat{\mu}_k^T\Sigma_T^{-1}\hat{\mu}_k\) 항이 더해졌기에 masking effect가 발생하였다. 마찬가지로 LDA에서는 이러한 문제가 발생하지 않았다.

Reduced Rank LDA

LDA의 discriminant function은 다음과 같다.

\[\underset{k}{\text{arg min}} \ \delta_k(x) = \underset{k}{\text{arg min}} \left[(x-\hat{\mu}_k)^T\hat{\Sigma}^{-1}(x-\hat{\mu}_k) - 2\log \pi_k \right]\]

이는 \(\hat{\Sigma}\)에 대하여 sphering (whitening)을 진행하면, prior를 고려하여 가장 가까운 centriod의 클래스가 예측값임을 알 수 있다. sphering trainformation은 다음과 같다.

\[X^* \leftarrow \mathbf{D}^{-\frac{1}{2}}\mathbf{U}^TX, \ \text{where} \ \hat{\Sigma} = \mathbf{U}\mathbf{D}\mathbf{U}^T\]

즉, centriod를 span하는 subspace에 \(X^*\)를 projection하여 결과를 비교해도 같은 결과를 낼 수 있다. \(K\)개의 클래스를 비교하는데 \((K-1)\)번의 단계만을 비교하면 되는 점을 생각하면 해당 subspace는 최대 \((K-1)\) 차원이고, 이를 \(H_{K-1}\)이라 하자. 이러한 projection은 특히 \(p\)가 \(K\)보다 훨씬 클 때 의미있을 것이다. 하지만 시각화를 하고 싶기에 차원 수를 2개로 줄이고 싶다거나, \(K \geq p\)에도 차원축소를 진행하고 싶을 것이다. 이러한 경우에는 이전 포스팅에서도 다뤘던 Principal Component를 활용하면 된다. 즉 sphering한 데이터의 centriod들의 subspace에 대한 principal component를 구한다.

1. 기존 클래스간 centroid들에 대한 \(K \times p\) 행렬 \(\mathbf{M}\)과 covariance matrix \(\mathbf{W}\) (within-class covariance)를 구한다.

2. \(\mathbf{W}\)의 고윳값 분해를 이용하여 \(\mathbf{M}^* = \mathbf{M}\mathbf{W}^{-\frac{1}{2}}\)를 계산한다.

3. principal component를 구하기 위해 \(\mathbf{M}^*\)의 covariance, 즉 between-class covariance \(\mathbf{B}^*\)를 구해 고윳값 분해 \(\mathbf{B}^* = \mathbf{V}^* \mathbf{D}_B {\mathbf{V}^*}^T\) 를 계산한다. 즉, \(\mathbf{V}^*\)의 각 컬럼 벡터 \(v_l^*\)들이 principal component direction이다.

종합해보면, \(l\)번째 discriminant variable은 \(Z_{l} = v_l^TX\)이다. (\(v_l = \mathbf{W}^{-\frac{1}{2}}v_l^*\)).

Fisher’s approach

Fisher는 위의 과정을 LDA에서의 정규분포에 대한 가정이 없이도, 다음과 같은 문제를 통해 같은 결론으로 도달하였다. 이는 within-class covariance와 비교하면서 between-class covariance를 최대화하는 선형 결합 \(Z = a^TX\)를 찾는 것이다. 왜 단순히 between-class covariance를 최대화 하는 것이 아닌 within-class covariance를 고려하는 이유는 다음 그림을 보면 이해가 갈 것이다.

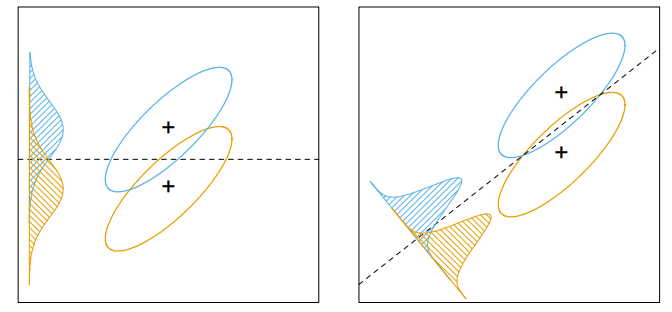
\(Z\)의 within-class covariance와 between-class covariance는 각각 \(a^T\mathbf{B}a, a^T\mathbf{W}a\)이기에 위 문제를 다시 다음과 같이 나타낼 수 있다.

\[\underset{a}{\mathrm{max}} \frac{a^T\mathbf{B}a}{a^T\mathbf{W}a}\]

이를 풀기 위해 먼저 \(\mathbf{W}\)에 대한 고유값 분해를 다음과 같이 해보자.

\[\mathbf{W} = \mathbf{V}_W \mathbf{D}_W \mathbf{V}_W^T = (\mathbf{D}_W^{\frac{1}{2}} \mathbf{V}_W^T)^T(\mathbf{D}_W^{\frac{1}{2}} \mathbf{V}_W^T) = {\mathbf{W}^{\frac{1}{2}}}^T\mathbf{W}^{\frac{1}{2}}\]

이를 위 식에 대입하면 다음과 같다.

\[\underset{a}{\mathrm{max}} \frac{a^T\mathbf{B}a}{a^T\mathbf{W}a} = \underset{b}{\mathrm{max}} \frac{b^T{\mathbf{W}^{-\frac{1}{2}}}^T\mathbf{B}\mathbf{W}^{-\frac{1}{2}}b}{b^Tb} = \underset{b}{\mathrm{max}} \frac{b^T\mathbf{B}^*b}{b^Tb} \text{ where } b=\mathbf{W}^{\frac{1}{2}}a\]

해당 식은 \(b\)의 스케일에 제한을 받지 않으므로, 라그랑지안을 이용하여 다음과 같이 풀 수 있다.

\[\underset{b}{\mathrm{max}} b^T\mathbf{B}^*b - \lambda(b^Tb - 1), \ \mathbf{B}^*b = \lambda b\]

즉, \(b\)는 \(\mathbf{B}^*\)의 고유벡터이므로 \(a = \mathbf{W}^{-\frac{1}{2}}v_1^*\)로 같은 결과를 도출해냈음을 알 수 있다.